Introdução à regressão de ridge

Na regressão linear múltipla ordinária, usamos um conjunto de p variáveis preditoras e uma variável de resposta para ajustar um modelo da forma:

Y = β ₀ + β ₁ X _{1 +} β ₂ X ₂ +… + β _p

Ouro:

• Y : A variável de resposta
• X _j : a j- ^ésima variável preditiva
• β _j : O efeito médio em Y de um aumento de uma unidade em X _j , mantendo todos os outros preditores fixos
• ε : O termo de erro

Os valores de β ₀ , β ₁ , B ₂ , …, β _p são escolhidos através do método dos mínimos quadrados , que minimiza a soma dos quadrados dos resíduos (RSS):

RSS = Σ(y _i – ŷ _i ) ²

Ouro:

• Σ : Um símbolo grego que significa soma
• y _i : o valor real da resposta para a ^i-ésima observação
• ŷ _i : O valor da resposta prevista com base no modelo de regressão linear múltipla

No entanto, quando as variáveis preditoras são altamente correlacionadas, a multicolinearidade pode se tornar um problema. Isso pode tornar as estimativas dos coeficientes do modelo pouco confiáveis e exibir alta variância.

Uma maneira de contornar esse problema sem remover completamente certas variáveis preditoras do modelo é usar um método conhecido como regressão de crista , que em vez disso busca minimizar o seguinte:

RSS + _λΣβj ²

onde j vai de 1 a p e λ ≥ 0.

Este segundo termo da equação é conhecido como penalidade de retirada .

Quando λ = 0, este termo de penalidade não tem efeito e a regressão de crista produz as mesmas estimativas de coeficiente que os mínimos quadrados. No entanto, à medida que λ se aproxima do infinito, a penalidade de contração torna-se mais influente e as estimativas do coeficiente de regressão de pico se aproximam de zero.

Em geral, as variáveis preditoras menos influentes no modelo diminuirão para zero mais rapidamente.

Por que usar a regressão Ridge?

A vantagem da regressão de Ridge sobre a regressão de mínimos quadrados é a compensação entre viés e variância .

Lembre-se de que o erro quadrático médio (MSE) é uma métrica que podemos usar para medir a precisão de um determinado modelo e é calculado da seguinte forma:

MSE = Var( f̂( x ₀ )) + [Bias( f̂( x ₀ ))] ² + Var(ε)

MSE = Variância + Viés ² + Erro irredutível

A ideia básica da regressão de Ridge é introduzir um pequeno viés para que a variância possa ser significativamente reduzida, levando a um MSE geral mais baixo.

Para ilustrar isso, considere o seguinte gráfico:

Observe que à medida que λ aumenta, a variância diminui significativamente com um aumento muito pequeno no viés. Porém, além de um certo ponto, a variância diminui menos rapidamente e a diminuição dos coeficientes leva a uma subestimação significativa dos mesmos, o que leva a um aumento acentuado do viés.

Podemos ver no gráfico que o MSE do teste é mais baixo quando escolhemos um valor para λ que produz um equilíbrio ideal entre viés e variância.

Quando λ = 0, o termo de penalidade na regressão de crista não tem efeito e, portanto, produz as mesmas estimativas de coeficiente que os mínimos quadrados. No entanto, aumentando λ até certo ponto, podemos reduzir o MSE geral do teste.

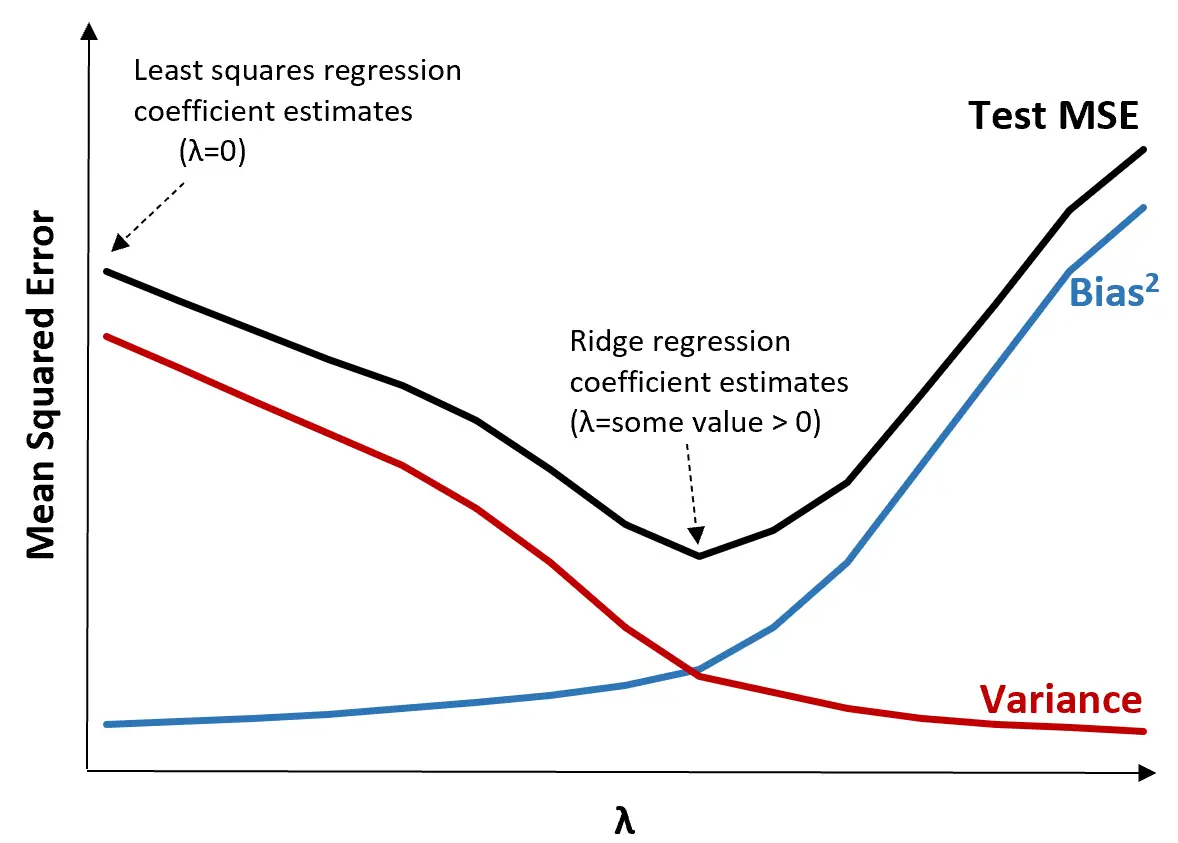
Isso significa que o ajuste do modelo por regressão de crista produzirá erros de teste menores do que o ajuste do modelo por regressão de mínimos quadrados.

Passos para realizar a regressão Ridge na prática

As etapas a seguir podem ser usadas para realizar a regressão de crista:

Etapa 1: Calcule a matriz de correlação e os valores VIF para as variáveis preditoras.

Primeiro, precisamos produzir uma matriz de correlação e calcular os valores VIF (fator de inflação de variância) para cada variável preditora.

Se detectarmos uma forte correlação entre as variáveis preditoras e valores altos de VIF (alguns textos definem um valor VIF “alto” como 5, enquanto outros usam 10), então a regressão de crista é provavelmente apropriada.

No entanto, se não houver multicolinearidade nos dados, pode não ser necessário realizar a regressão de cristas em primeiro lugar. Em vez disso, podemos realizar a regressão de mínimos quadrados ordinária.

Etapa 2: padronize cada variável preditora.

Antes de realizar a regressão de crista, precisamos dimensionar os dados de forma que cada variável preditora tenha uma média de 0 e um desvio padrão de 1. Isso garante que nenhuma variável preditora tenha uma influência excessiva ao executar uma regressão de crista.

Etapa 3: ajuste o modelo de regressão de crista e escolha um valor para λ.

Não existe uma fórmula exata que possamos usar para determinar qual valor usar para λ. Na prática, existem duas maneiras comuns de escolher λ:

(1) Crie um gráfico de rastreamento Ridge. Este é um gráfico que visualiza os valores das estimativas dos coeficientes à medida que λ aumenta em direção ao infinito. Normalmente, escolhemos λ como o valor no qual a maioria das estimativas dos coeficientes começa a estabilizar.

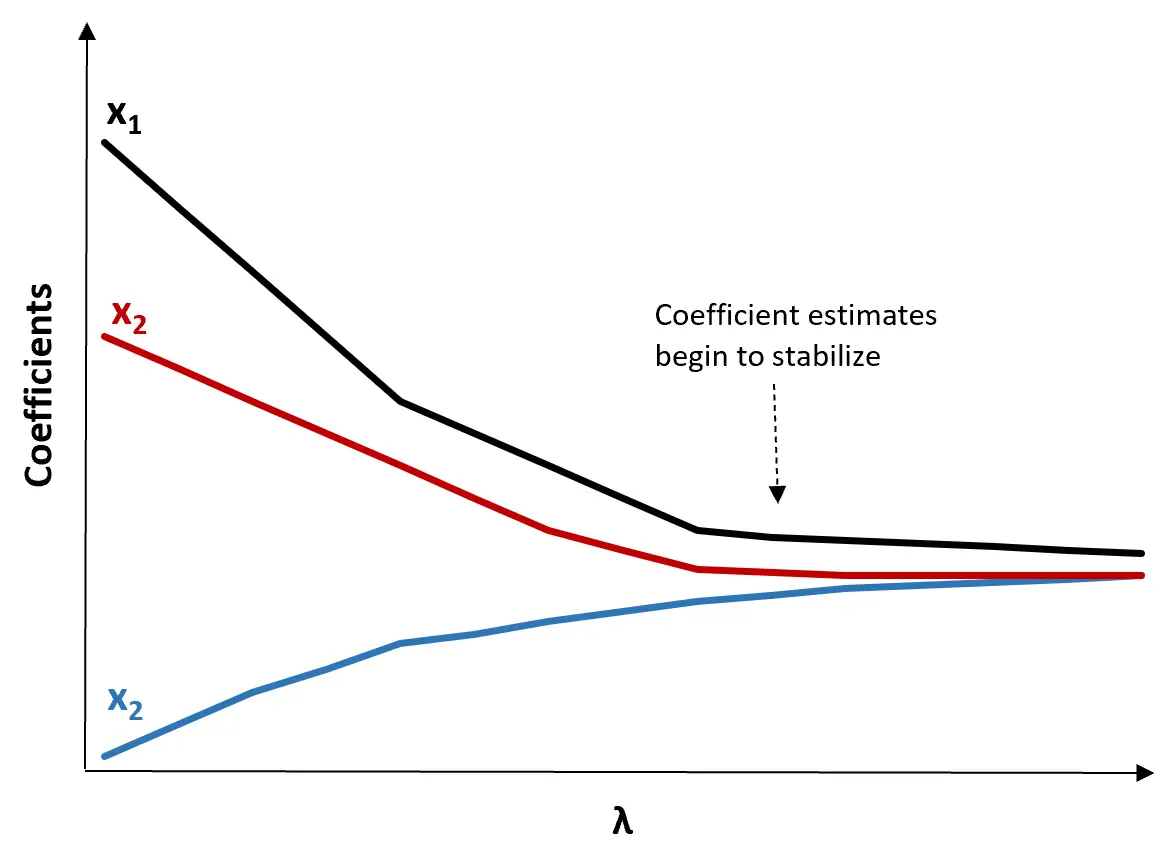
(2) Calcule o teste MSE para cada valor de λ.

Outra forma de escolher λ é simplesmente calcular o MSE de teste de cada modelo com diferentes valores de λ e escolher λ como o valor que produz o menor MSE de teste.

Vantagens e desvantagens da regressão Ridge

A maior vantagem da regressão de Ridge é sua capacidade de produzir um erro quadrático médio (MSE) de teste mais baixo do que os mínimos quadrados quando a multicolinearidade está presente.

No entanto, a maior desvantagem da regressão de Ridge é a sua incapacidade de realizar a seleção de variáveis, uma vez que inclui todas as variáveis preditoras no modelo final. Como alguns preditores serão reduzidos para muito perto de zero, isso pode dificultar a interpretação dos resultados do modelo.

Na prática, a regressão de Ridge tem o potencial de produzir um modelo capaz de fazer melhores previsões em comparação com um modelo de mínimos quadrados, mas muitas vezes é mais difícil de interpretar os resultados do modelo.

Dependendo se a interpretação do modelo ou a precisão da previsão são mais importantes para você, você pode optar por usar mínimos quadrados comuns ou regressão de crista em diferentes cenários.

Regressão Ridge em R e Python

Os tutoriais a seguir explicam como realizar a regressão de crista em R e Python, as duas linguagens mais comumente usadas para ajustar modelos de regressão de crista:

Regressão Ridge em R (passo a passo)
Regressão Ridge em Python (passo a passo)