Introdução à regressão laço
Na regressão linear múltipla ordinária, usamos um conjunto de p variáveis preditoras e uma variável de resposta para ajustar um modelo da forma:
Y = β 0 + β 1 X 1 + β 2 X 2 +… + β p
Ouro:
- Y : A variável de resposta
- X j : a j- ésima variável preditiva
- β j : O efeito médio em Y de um aumento de uma unidade em X j , mantendo todos os outros preditores fixos
- ε : O termo de erro
Os valores de β 0 , β 1 , B 2 , …, β p são escolhidos através do método dos mínimos quadrados , que minimiza a soma dos quadrados dos resíduos (RSS):
RSS = Σ(y i – ŷ i ) 2
Ouro:
- Σ : Um símbolo grego que significa soma
- y i : o valor real da resposta para a i-ésima observação
- ŷ i : O valor da resposta prevista com base no modelo de regressão linear múltipla
No entanto, quando as variáveis preditoras são altamente correlacionadas, a multicolinearidade pode se tornar um problema. Isso pode tornar as estimativas dos coeficientes do modelo pouco confiáveis e exibir alta variância. Ou seja, quando o modelo é aplicado a um novo conjunto de dados que nunca viu antes, é provável que tenha um desempenho insatisfatório.
Uma maneira de contornar esse problema é usar um método conhecido como regressão laço , que busca minimizar o seguinte:
RSS + λΣ|β j |
onde j vai de 1 a p e λ ≥ 0.
Este segundo termo da equação é conhecido como penalidade de retirada .
Quando λ = 0, este termo de penalidade não tem efeito e a regressão laço produz as mesmas estimativas de coeficiente que os mínimos quadrados.
No entanto, à medida que λ se aproxima do infinito, a penalidade de remoção torna-se mais influente e as variáveis preditivas que não são importáveis para o modelo são reduzidas a zero e algumas são até removidas do modelo.
Por que usar a regressão Lasso?
A vantagem da regressão laço sobre a regressão de mínimos quadrados é a compensação entre viés e variância .
Lembre-se de que o erro quadrático médio (MSE) é uma métrica que podemos usar para medir a precisão de um determinado modelo e é calculado da seguinte forma:
MSE = Var( f̂( x 0 )) + [Bias( f̂( x 0 ))] 2 + Var(ε)
MSE = Variância + Viés 2 + Erro irredutível
A ideia básica da regressão laço é introduzir um pequeno viés para que a variância possa ser significativamente reduzida, levando a um MSE geral mais baixo.
Para ilustrar isso, considere o seguinte gráfico:

Observe que à medida que λ aumenta, a variância diminui significativamente com um aumento muito pequeno no viés. Porém, além de um certo ponto, a variância diminui menos rapidamente e a diminuição dos coeficientes leva a uma subestimação significativa dos mesmos, o que leva a um aumento acentuado do viés.
Podemos ver no gráfico que o MSE do teste é mais baixo quando escolhemos um valor para λ que produz um equilíbrio ideal entre viés e variância.
Quando λ = 0, o termo de penalidade na regressão laço não tem efeito e, portanto, produz as mesmas estimativas de coeficiente que os mínimos quadrados. No entanto, aumentando λ até certo ponto, podemos reduzir o MSE geral do teste.
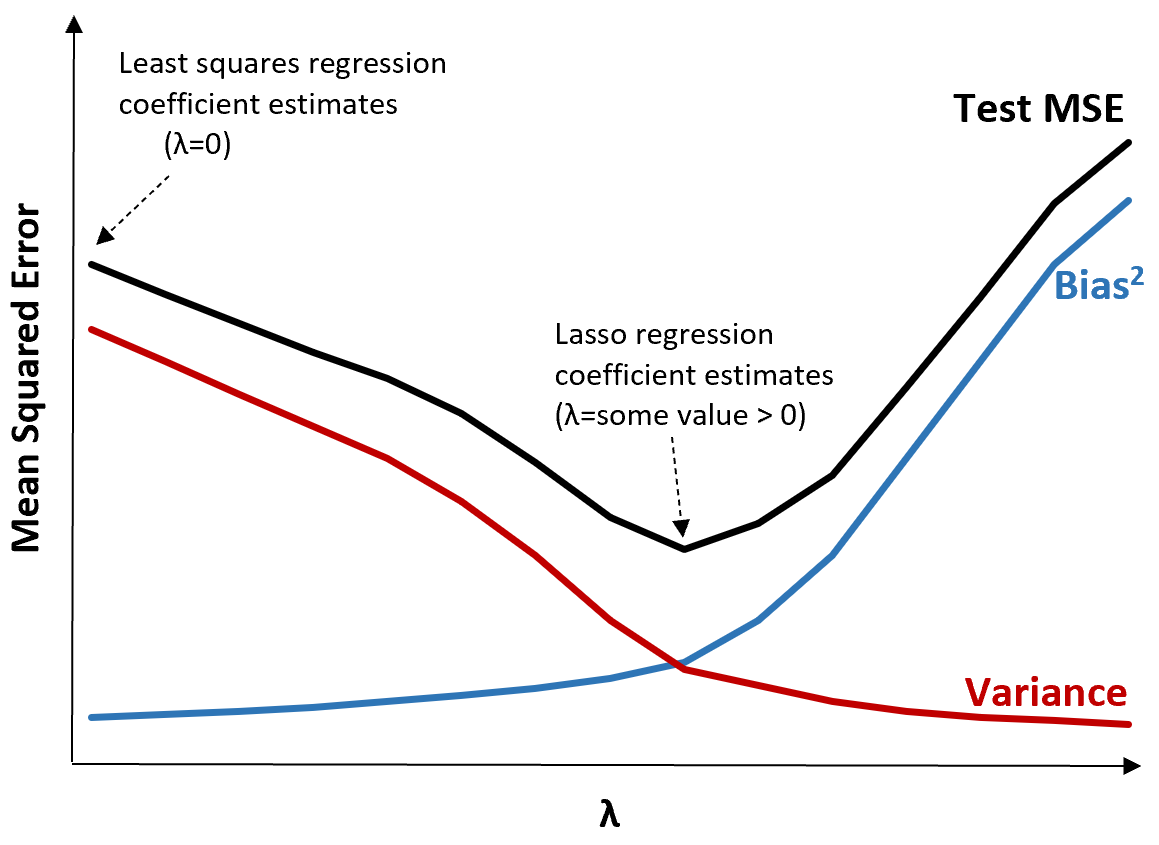
Isso significa que o ajuste do modelo por regressão laço produzirá erros de teste menores do que o ajuste do modelo por regressão de mínimos quadrados.
Regressão Lasso vs Regressão Ridge
A regressão Lasso e a regressão Ridge são conhecidas como métodos de regularização porque ambas tentam minimizar a soma residual dos quadrados (RSS), bem como um determinado termo de penalidade.
Em outras palavras, restringem ou regularizam as estimativas dos coeficientes do modelo.
No entanto, os termos de penalidade que eles usam são um pouco diferentes:
- A regressão Lasso tenta minimizar RSS + λΣ|β j |
- A regressão Ridge tenta minimizar RSS + λΣβ j 2
Quando usamos a regressão de crista, os coeficientes de cada preditor são reduzidos a zero, mas nenhum deles pode chegar completamente a zero .
Por outro lado, quando usamos a regressão laço, é possível que alguns coeficientes se tornem completamente zero quando λ se tornar grande o suficiente.
Em termos técnicos, a regressão laço é capaz de produzir modelos “esparsos”, ou seja, modelos que incluem apenas um subconjunto de variáveis preditoras.
Isso levanta a questão: a regressão de crista ou a regressão de laço são melhores?
A resposta: depende!
Nos casos em que apenas um pequeno número de variáveis preditoras são significativas, a regressão laço tende a funcionar melhor porque é capaz de reduzir completamente as variáveis insignificantes a zero e removê-las do modelo.
No entanto, quando muitas variáveis preditoras são significativas no modelo e seus coeficientes são aproximadamente iguais, a regressão de crista tende a funcionar melhor porque mantém todos os preditores no modelo.
Para determinar qual modelo é mais eficaz em fazer previsões, realizamos validação cruzada k-fold . Qualquer modelo que produza o menor erro quadrático médio (MSE) é o melhor modelo a ser usado.
Etapas para realizar uma regressão laço na prática
As etapas a seguir podem ser usadas para realizar uma regressão laço:
Etapa 1: Calcule a matriz de correlação e os valores VIF para as variáveis preditoras.
Primeiro, precisamos produzir uma matriz de correlação e calcular os valores VIF (fator de inflação de variância) para cada variável preditora.
Se detectarmos uma forte correlação entre as variáveis preditoras e valores altos de VIF (alguns textos definem um valor VIF “alto” como 5, enquanto outros usam 10), então a regressão laço é provavelmente apropriada.
No entanto, se não houver multicolinearidade nos dados, pode não haver necessidade de realizar a regressão laço em primeiro lugar. Em vez disso, podemos realizar a regressão de mínimos quadrados ordinária.
Etapa 2: ajuste o modelo de regressão laço e escolha um valor para λ.
Depois de determinarmos que a regressão laço é apropriada, podemos ajustar o modelo (usando linguagens de programação populares como R ou Python) usando o valor ideal para λ.
Para determinar o valor ideal para λ, podemos ajustar vários modelos usando valores diferentes para λ e escolher λ como o valor que produz o teste MSE mais baixo.
Etapa 3: compare a regressão laço com a regressão de crista e a regressão de mínimos quadrados ordinários.
Finalmente, podemos comparar nosso modelo de regressão laço com um modelo de regressão de crista e um modelo de regressão de mínimos quadrados para determinar qual modelo produz o teste MSE mais baixo usando validação cruzada k-fold.
Dependendo da relação entre as variáveis preditoras e a variável resposta, é perfeitamente possível que um destes três modelos supere os outros em diferentes cenários.
Regressão Lasso em R e Python
Os tutoriais a seguir explicam como realizar a regressão laço em R e Python:
Regressão Lasso em R (passo a passo)
Regressão Lasso em Python (passo a passo)