Como realizar regressão linear múltipla no excel

A regressão linear múltipla é um método que podemos usar para compreender a relação entre duas ou mais variáveis explicativas e uma variável de resposta .

Este tutorial explica como realizar regressão linear múltipla no Excel.

Nota: Se você tiver apenas uma variável explicativa, deverá realizar uma regressão linear simples .

Exemplo: regressão linear múltipla no Excel

Suponha que queiramos saber se o número de horas de estudo e o número de exames preparatórios realizados afetam a nota que um aluno obtém em determinado vestibular.

Para explorar essa relação, podemos realizar uma regressão linear múltipla utilizando horas estudadas e exames preparatórios tomados como variáveis explicativas e resultados de exames como variável resposta.

Conclua as etapas a seguir no Excel para realizar a regressão linear múltipla.

Passo 1: Insira os dados.

Insira os seguintes dados para o número de horas estudadas, exames preparatórios realizados e resultados de exames recebidos para 20 alunos:

Etapa 2: Execute a regressão linear múltipla.

Na faixa superior do Excel, vá para a guia Dados e clique em Análise de Dados . Se você não vir essa opção, primeiro instale o software Analysis ToolPak gratuito .

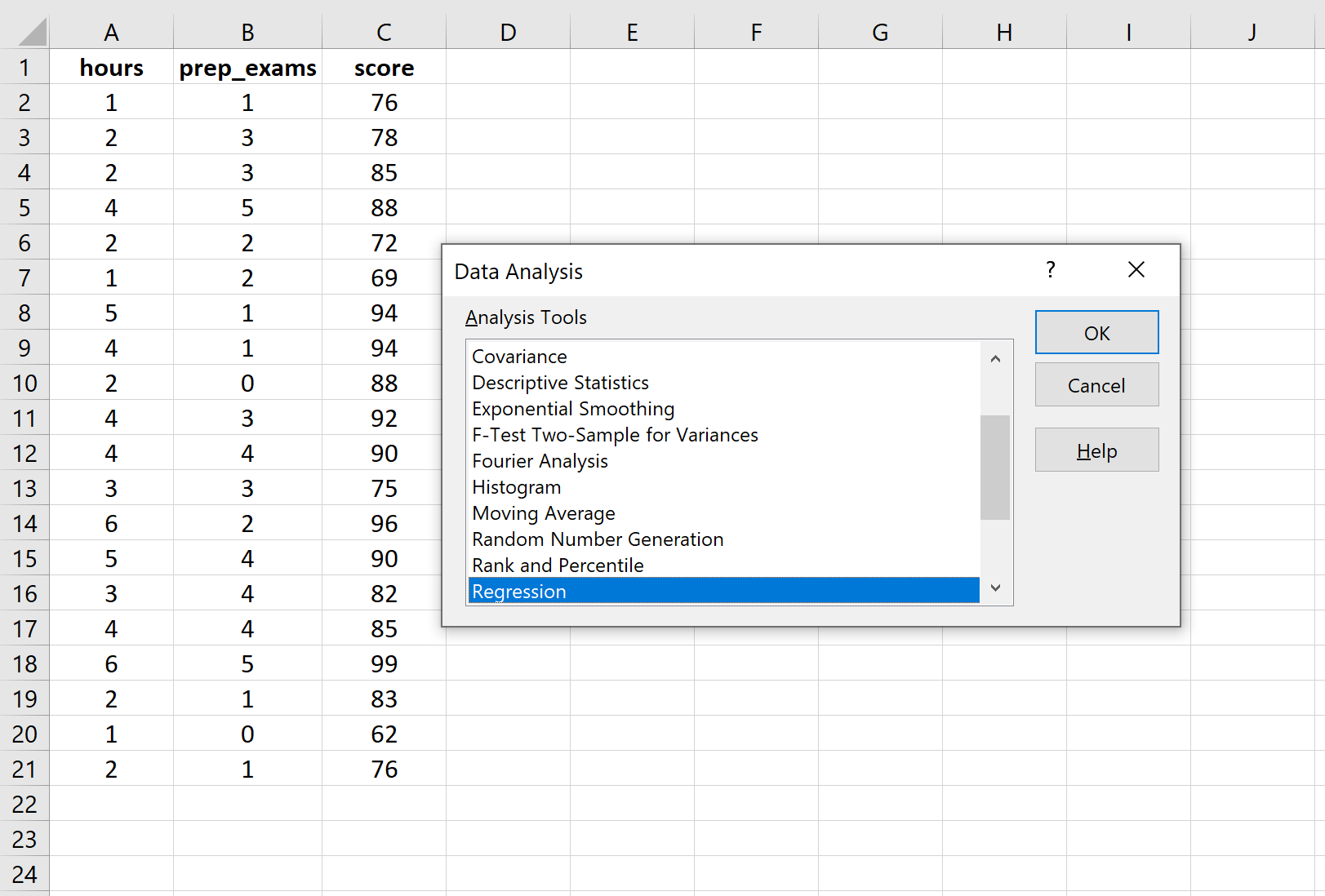
Depois de clicar em Análise de Dados, uma nova janela aparecerá. Selecione Regressão e clique em OK.

Para Input Y Range , preencha a matriz de valores da variável de resposta. Para Input X Range , preencha a matriz de valores das duas variáveis explicativas. Marque a caixa ao lado de Rótulos para informar ao Excel que incluímos os nomes das variáveis nos intervalos de entrada. Para Output Range , selecione uma célula na qual deseja que a saída da regressão apareça. Em seguida, clique em OK .

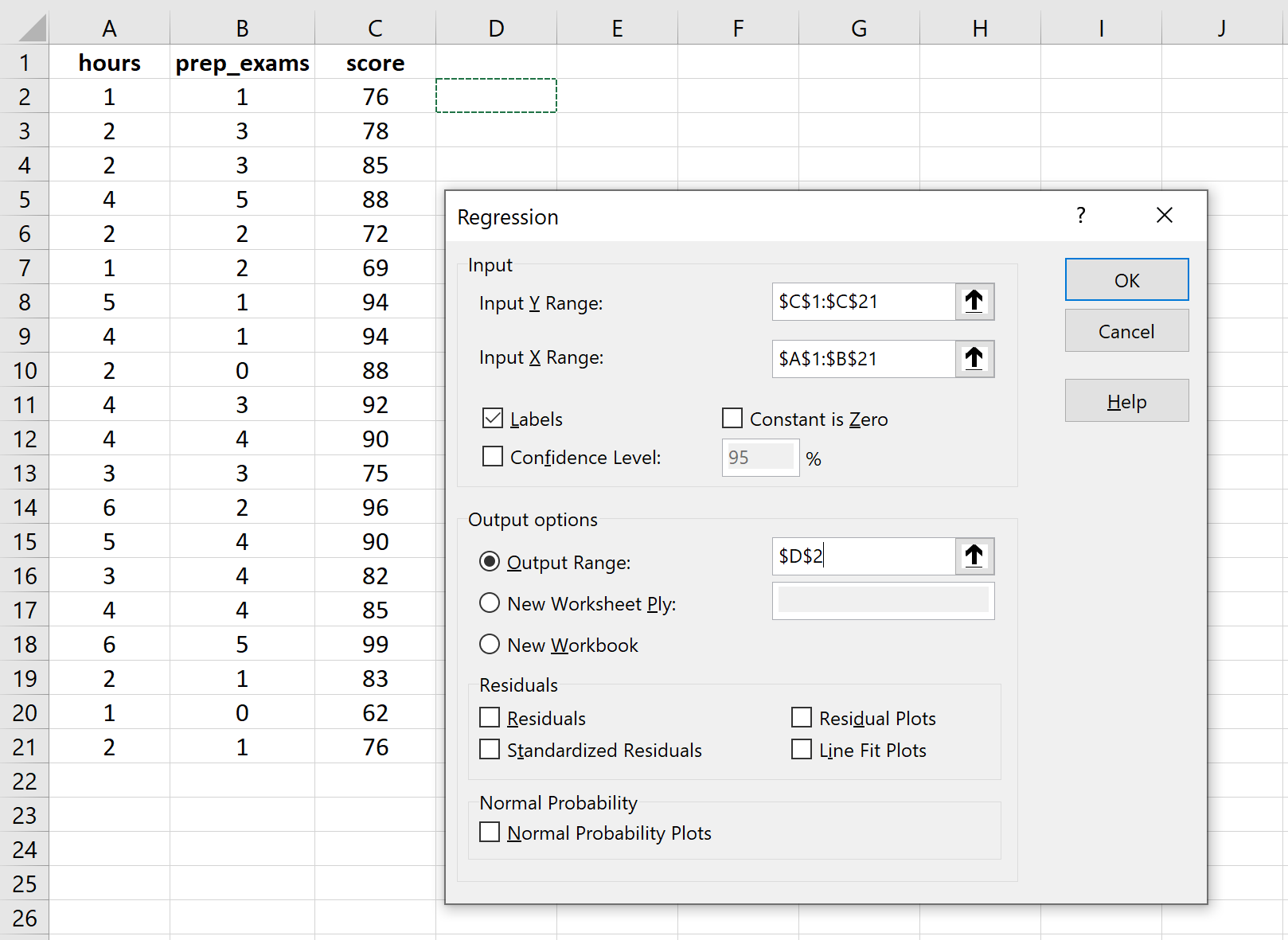
A seguinte saída aparecerá automaticamente:

Etapa 3: interprete o resultado.

Veja como interpretar os números mais relevantes no resultado:

R Quadrado: 0,734 . Isso é chamado de coeficiente de determinação. É a proporção da variância da variável resposta que pode ser explicada pelas variáveis explicativas. Neste exemplo, 73,4% da variação nas notas dos exames é explicada pela quantidade de horas estudadas e pela quantidade de exames preparatórios realizados.

Erro padrão: 5,366 . Esta é a distância média entre os valores observados e a linha de regressão. Neste exemplo, os valores observados desviam-se em média 5.366 unidades da linha de regressão.

F: 23h46 Esta é a estatística F geral para o modelo de regressão, calculada como regressão MS/MS residual.

Significado F: 0,0000 . Este é o valor p associado à estatística F geral. Isto nos diz se o modelo de regressão como um todo é estatisticamente significativo ou não. Por outras palavras, diz-nos se as duas variáveis explicativas combinadas têm uma associação estatisticamente significativa com a variável resposta. Neste caso, o valor p é inferior a 0,05, indicando que as variáveis explicativas , horas estudadas e exames preparatórios realizados em conjunto, têm associação estatisticamente significativa com o resultado do exame .

Valores P. Os valores p individuais nos dizem se cada variável explicativa é estatisticamente significativa ou não. Podemos perceber que as horas estudadas são estatisticamente significativas (p = 0,00) enquanto os exames preparatórios realizados (p = 0,52) não são estatisticamente significativos para α = 0,05. Como os exames preparatórios anteriores não são estatisticamente significativos, podemos acabar decidindo retirá-los do modelo.

Coeficientes: Os coeficientes de cada variável explicativa nos informam a mudança média esperada na variável de resposta, assumindo que a outra variável explicativa permaneça constante. Por exemplo, para cada hora adicional gasta estudando, espera-se que a pontuação média do exame aumente em 5,56 , assumindo que os exames práticos realizados permaneçam constantes.

Aqui está outra maneira de ver isso: se o aluno A e o aluno B fizerem o mesmo número de exames preparatórios, mas o aluno A estudar uma hora a mais, então o aluno A deverá pontuar 5,56 pontos a mais do que o aluno B.

Interpretamos o coeficiente de interceptação como significando que a nota esperada no exame para um aluno que não estuda horas e não faz exames preparatórios é 67,67 .

Equação de regressão estimada: podemos usar os coeficientes do resultado do modelo para criar a seguinte equação de regressão estimada:

nota do exame = 67,67 + 5,56*(horas) – 0,60*(exames preparatórios)

Podemos usar esta equação de regressão estimada para calcular a pontuação esperada no exame de um aluno, com base no número de horas de estudo e no número de exames práticos que ele faz. Por exemplo, um aluno que estuda três horas e faz um exame preparatório deverá obter nota 83,75 :

nota do exame = 67,67 + 5,56*(3) – 0,60*(1) = 83,75

Lembre-se de que, como os exames preparatórios anteriores não foram estatisticamente significativos (p = 0,52), podemos decidir removê-los, pois não proporcionam nenhuma melhoria ao modelo geral. Neste caso, poderíamos realizar uma regressão linear simples utilizando apenas as horas estudadas como variável explicativa.

Os resultados desta análise de regressão linear simples podem ser encontrados aqui .

Recursos adicionais

Depois de realizar a regressão linear múltipla, você pode verificar várias suposições, incluindo:

1. Teste de multicolinearidade usando VIF .

2. Teste de heterocedasticidade usando um teste de Breusch-Pagan .

3. Teste a normalidade usando um gráfico QQ .