Regressão linear simples

Este artigo explica o que é regressão linear simples em estatística e como ela é executada. Da mesma forma, você encontrará um exercício de regressão linear simples resolvido e, além disso, uma calculadora de regressão linear simples online.

O que é regressão linear simples?

A regressão linear simples é um modelo estatístico usado para relacionar uma variável independente e tentamos aproximar a relação que existe entre as duas variáveis.

Portanto, a regressão linear simples é usada para encontrar uma equação que relacione duas variáveis linearmente. Logicamente, a relação entre as duas variáveis deve ser linear, caso contrário outro tipo de modelo de regressão deve ser utilizado.

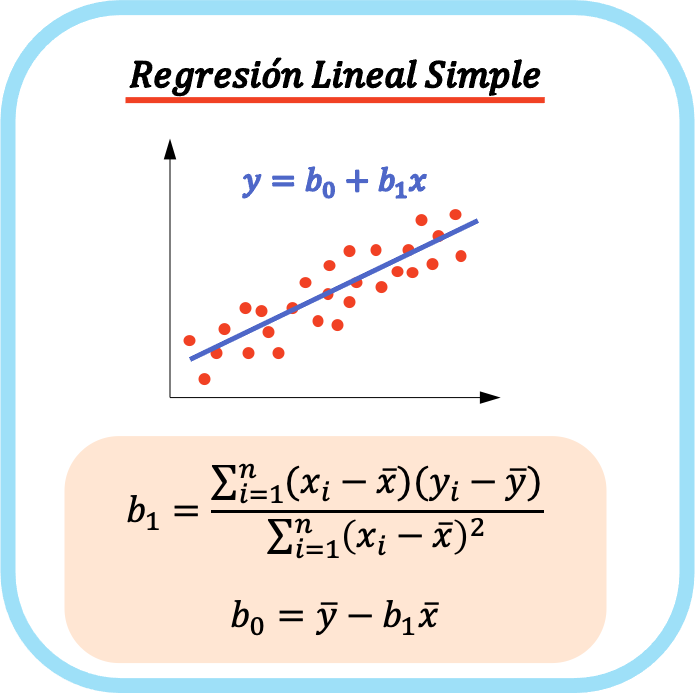
A equação de um modelo de regressão linear simples é composta por dois coeficientes: a constante da equação (b ₀ ) e o coeficiente de correlação entre as duas variáveis (b ₁ ). Portanto, a equação para um modelo de regressão linear simples é y=b ₀ +b ₁ x.

A equação para uma regressão linear simples é representada graficamente como uma linha reta, então o coeficiente b ₀ é a interceptação e o coeficiente b ₁ é a inclinação da linha.

Fórmulas de regressão linear simples

As fórmulas para calcular os coeficientes de uma regressão linear simples são as seguintes:

👉 Você pode usar a calculadora abaixo para calcular os coeficientes de uma regressão linear simples para qualquer conjunto de dados.

Obviamente, a equação resultante do modelo de regressão linear simples não será capaz de adivinhar o valor exato de todas as observações, uma vez que este modelo simplesmente tenta encontrar uma equação que aproxime a relação entre as duas variáveis. Assim, o resíduo é definido como a diferença entre o valor verdadeiro e o valor estimado pelo modelo de regressão linear.

Observe que o objetivo de um modelo de regressão linear simples é minimizar os quadrados dos resíduos, ou seja, a regressão linear simples é baseada no critério dos mínimos quadrados .

Exemplo concreto de regressão linear simples

Para finalizar o entendimento do método de regressão linear simples, aqui está um exemplo prático passo a passo em que a equação de um modelo de regressão linear simples é calculada a partir de um conjunto de dados estatísticos.

• Depois de fazer um exame de estatística, cinco alunos foram questionados sobre quantas horas de estudo haviam dedicado ao exame. Os dados são apresentados na tabela abaixo. Execute um modelo de regressão linear simples dos dados estatísticos coletados para relacionar linearmente as horas de estudo com a nota alcançada.

Para realizar um modelo de regressão linear simples devemos determinar os coeficientes b ₀ e b ₁ da equação e, para isso, devemos utilizar as fórmulas vistas na seção acima.

Porém, para aplicar as fórmulas de regressão linear simples, devemos primeiro calcular a média da variável independente e a média da variável dependente:

Agora que conhecemos as médias das variáveis, calculamos o coeficiente b ₁ do modelo utilizando sua fórmula correspondente:

Por fim, calculamos o coeficiente b ₀ do modelo utilizando sua fórmula correspondente:

Resumindo, a equação para o modelo de regressão linear simples do problema é:

Abaixo você pode ver a representação gráfica dos dados amostrais, bem como a reta do modelo de regressão linear simples:

Por fim, uma vez calculada a equação do modelo de regressão linear simples, resta interpretar o resultado obtido. Para isso é fundamental calcular o coeficiente de determinação do modelo de regressão, você pode ver como isso é feito pesquisando o artigo correspondente em nosso site.

Suposições de regressão linear simples

Para realizar uma regressão linear simples, as seguintes suposições devem ser atendidas:

• Independência : os resíduos observados devem ser independentes entre si. Uma maneira comum de garantir a independência do modelo é adicionar aleatoriedade ao processo de amostragem.
• Homocedasticidade : Deve haver homogeneidade nas variâncias dos resíduos, ou seja, a variabilidade dos resíduos deve ser constante.
• Normalidade : Os resíduos devem ter distribuição normal, ou seja, devem seguir uma distribuição normal com média 0.
• Linearidade – A relação entre a variável independente e a variável dependente deve ser linear.

Calculadora de regressão linear simples

Insira dados de amostra na calculadora abaixo para ajustar um modelo de regressão linear simples entre duas variáveis. É necessário separar os pares de dados, para que na primeira caixa existam apenas os valores da variável independente X e na segunda caixa existam apenas os valores da variável dependente Y.

Os dados devem ser separados por espaço e inseridos usando o ponto final como separador decimal.

Regressão linear simples e múltipla

Por fim, veremos qual a diferença entre regressão linear simples e regressão linear múltipla, pois são dois tipos de regressões lineares frequentemente utilizadas em estatística.

A regressão linear múltipla permite vincular matematicamente duas ou mais variáveis explicativas a uma variável de resposta. Ou seja, na regressão linear múltipla cria-se um modelo no qual existem pelo menos duas variáveis independentes.

Portanto, a diferença entre a regressão linear simples e a regressão linear múltipla é o número de variáveis independentes. Na regressão linear simples, existe apenas uma variável independente, enquanto na regressão linear múltipla, existem duas ou mais variáveis independentes.