Como realizar regressão linear simples em python (passo a passo)

A regressão linear simples é uma técnica que podemos usar para compreender a relação entre uma única variável explicativa e uma única variável de resposta .

Esta técnica encontra a linha que melhor “se ajusta” aos dados e assume a seguinte forma:

ŷ=b ₀ + b ₁ x

Ouro:

• ŷ : O valor estimado da resposta
• b ₀ : A origem da linha de regressão
• b ₁ : A inclinação da linha de regressão

Esta equação pode ajudar-nos a compreender a relação entre a variável explicativa e a variável de resposta e (assumindo que seja estatisticamente significativa) pode ser usada para prever o valor de uma variável de resposta dado o valor da variável explicativa.

Este tutorial fornece uma explicação passo a passo sobre como realizar regressão linear simples em Python.

Etapa 1: carregar dados

Para este exemplo, criaremos um conjunto de dados falso contendo as duas variáveis a seguir para 15 alunos:

• Número total de horas estudadas para determinados exames
• Resultado de exame

Tentaremos ajustar um modelo de regressão linear simples usando horas como variável explicativa e resultados de exames como variável resposta.

O código a seguir mostra como criar esse conjunto de dados falso em Python:

 import pandas as pd

#create dataset
df = pd. DataFrame ({' hours ': [1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14],
                   ' score ': [64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89]})
      

#view first six rows of dataset
df[0:6]

    hours score
0 1 64
1 2 66
2 4 76
3 5 73
4 5 74
5 6 81

Etapa 2: visualize os dados

Antes de ajustar um modelo de regressão linear simples, devemos primeiro visualizar os dados para entendê-los.

Primeiro, queremos garantir que a relação entre horas e pontuação seja aproximadamente linear, uma vez que esta é uma suposição subjacente da regressão linear simples.

Podemos criar um gráfico de dispersão simples para visualizar a relação entre as duas variáveis:

 import matplotlib.pyplot as plt

plt. scatter (df.hours, df.score)
plt. title (' Hours studied vs. Exam Score ')
plt. xlabel (' Hours ')
plt. ylabel (' Score ')
plt. show ()

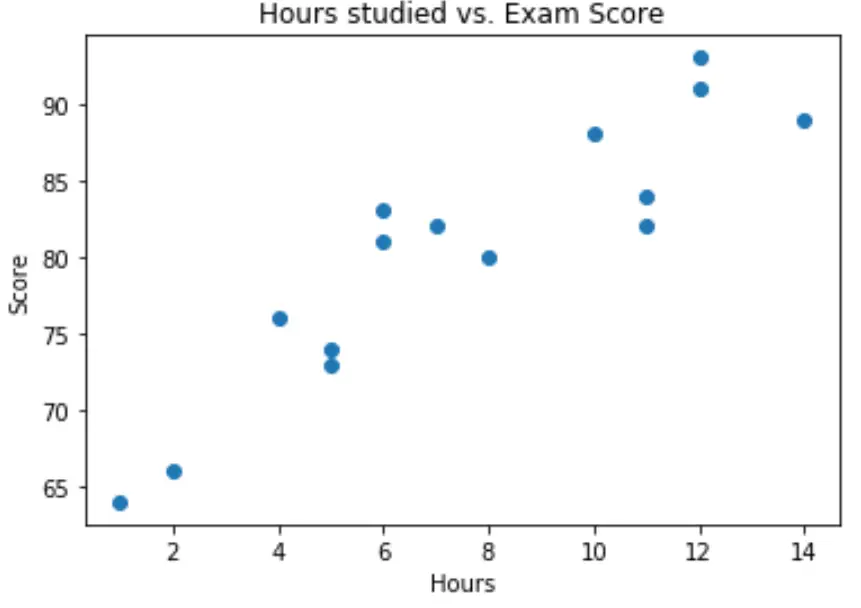
No gráfico podemos ver que a relação parece ser linear. À medida que o número de horas aumenta, a pontuação também tende a aumentar linearmente.

Depois podemos criar um boxplot para visualizar a distribuição dos resultados dos exames e verificar se há outliers . Por padrão, Python define uma observação como outlier se for 1,5 vezes o intervalo interquartil acima do terceiro quartil (Q3) ou 1,5 vezes o intervalo interquartil abaixo do primeiro quartil (Q1).

Se uma observação for atípica, um pequeno círculo aparecerá no boxplot:

 df. boxplot (column=[' score ']) 

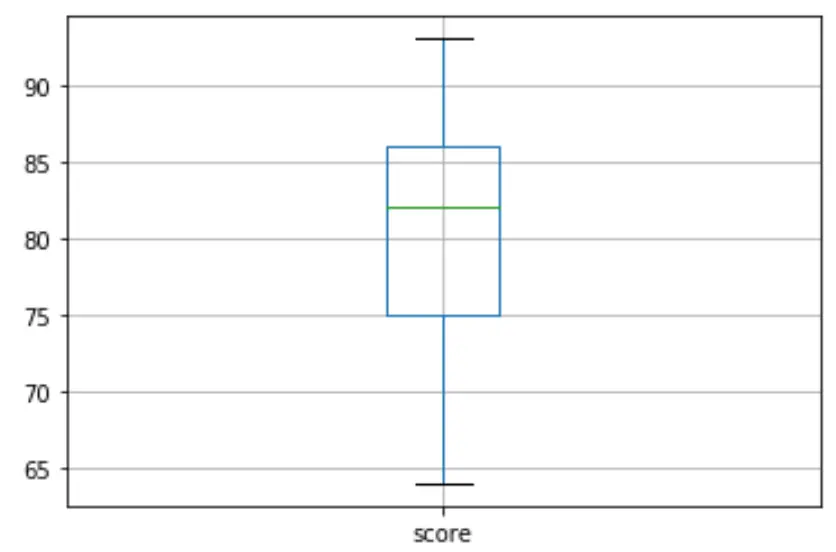
Não há pequenos círculos no boxplot, o que significa que não há valores discrepantes em nosso conjunto de dados.

Etapa 3: execute uma regressão linear simples

Depois de confirmarmos que a relação entre nossas variáveis é linear e não há outliers, podemos proceder ao ajuste de um modelo de regressão linear simples usando horas como variável explicativa e a pontuação como variável de resposta:

Nota: Usaremos a função OLS() da biblioteca statsmodels para ajustar o modelo de regressão.

 import statsmodels.api as sm

#define response variable
y = df[' score ']

#define explanatory variable
x = df[[' hours ']]

#add constant to predictor variables
x = sm. add_constant (x)

#fit linear regression model
model = sm. OLS (y,x). fit ()

#view model summary
print ( model.summary ())

                            OLS Regression Results                            
==================================================== ============================
Dept. Variable: R-squared score: 0.831
Model: OLS Adj. R-squared: 0.818
Method: Least Squares F-statistic: 63.91
Date: Mon, 26 Oct 2020 Prob (F-statistic): 2.25e-06
Time: 15:51:45 Log-Likelihood: -39,594
No. Observations: 15 AIC: 83.19
Df Residuals: 13 BIC: 84.60
Model: 1                                         
Covariance Type: non-robust                                         
==================================================== ============================
                 coef std err t P>|t| [0.025 0.975]
-------------------------------------------------- ----------------------------
const 65.3340 2.106 31.023 0.000 60.784 69.884
hours 1.9824 0.248 7.995 0.000 1.447 2.518
==================================================== ============================
Omnibus: 4,351 Durbin-Watson: 1,677
Prob(Omnibus): 0.114 Jarque-Bera (JB): 1.329
Skew: 0.092 Prob(JB): 0.515
Kurtosis: 1.554 Cond. No. 19.2
==================================================== ============================

A partir do resumo do modelo, podemos ver que a equação de regressão ajustada é:

Pontuação = 65,334 + 1,9824*(horas)

Isso significa que cada hora adicional estudada está associada a um aumento médio na pontuação do exame de 1,9824 pontos. E o valor original de 65.334 nos indica a nota média esperada no exame para um aluno que estuda zero horas.

Também podemos usar essa equação para encontrar a pontuação esperada no exame com base no número de horas que um aluno estuda. Por exemplo, um aluno que estuda 10 horas deverá obter nota 85.158 no exame:

Pontuação = 65,334 + 1,9824*(10) = 85,158

Veja como interpretar o restante do resumo do modelo:

• P>|t| : Este é o valor p associado aos coeficientes do modelo. Como o valor p para horas (0,000) é significativamente menor que 0,05, podemos afirmar que existe uma associação estatisticamente significativa entre horas e pontuação .
• R-quadrado: Este número nos diz que o percentual de variação nas notas dos exames pode ser explicado pelo número de horas estudadas. Em geral, quanto maior o valor de R ao quadrado de um modelo de regressão, melhor as variáveis explicativas são capazes de prever o valor da variável resposta. Nesse caso, 83,1% da variação nas notas é explicada pelas horas estudadas.
• Estatística F e valor p: A estatística F ( 63,91 ) e o valor p correspondente ( 2,25e-06 ) nos dizem a significância geral do modelo de regressão, ou seja, se as variáveis explicativas no modelo são úteis para explicar a variação . na variável de resposta. Como o valor p neste exemplo é inferior a 0,05, nosso modelo é estatisticamente significativo e as horas são consideradas úteis para explicar a variação da pontuação .

Etapa 4: criar gráficos residuais

Após ajustar o modelo de regressão linear simples aos dados, a etapa final é criar gráficos residuais.

Uma das principais suposições da regressão linear é que os resíduos de um modelo de regressão são distribuídos aproximadamente normalmente e são homocedásticos em cada nível da variável explicativa. Se estes pressupostos não forem cumpridos, os resultados do nosso modelo de regressão poderão ser enganadores ou pouco fiáveis.

Para verificar se essas suposições são atendidas, podemos criar os seguintes gráficos residuais:

Gráfico de resíduos versus valores ajustados: Este gráfico é útil para confirmar a homocedasticidade. O eixo x exibe os valores ajustados e o eixo y exibe os resíduos. Contanto que os resíduos pareçam estar distribuídos de forma aleatória e uniforme ao longo do gráfico em torno do valor zero, podemos assumir que a homocedasticidade não é violada:

 #define figure size
fig = plt. figure (figsize=(12.8))

#produce residual plots
fig = sm.graphics. plot_regress_exog (model, ' hours ', fig=fig)

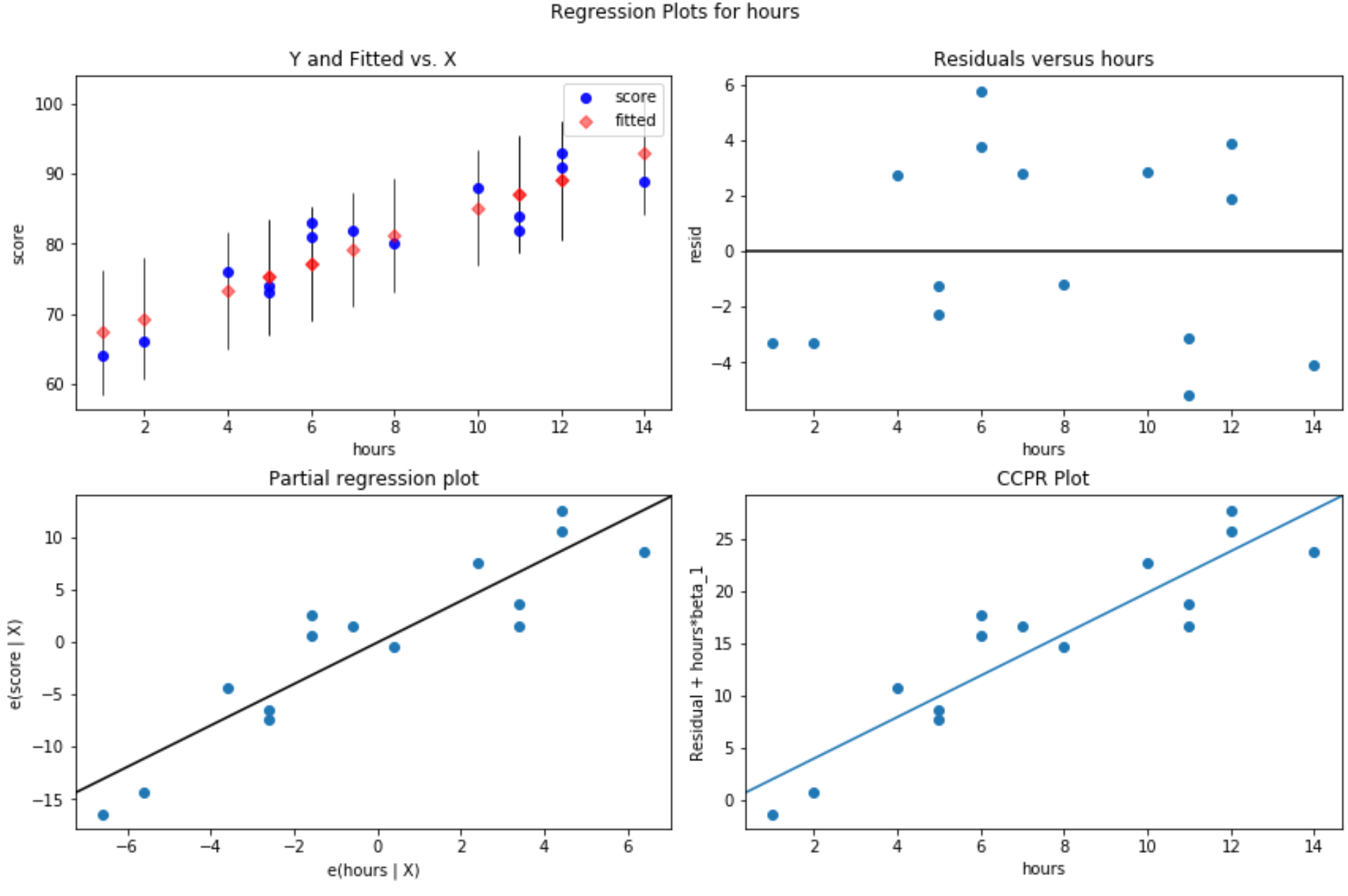
Quatro parcelas são produzidas. O que está no canto superior direito é o gráfico residual versus o gráfico ajustado. O eixo x neste gráfico mostra os valores reais dos pontos da variável preditora e o eixo y mostra o resíduo para esse valor.

Como os resíduos parecem estar espalhados aleatoriamente em torno de zero, isso indica que a heterocedasticidade não é um problema com a variável explicativa.

Gráfico QQ: Este gráfico é útil para determinar se os resíduos seguem uma distribuição normal. Se os valores dos dados no gráfico seguirem uma linha aproximadamente reta em um ângulo de 45 graus, os dados serão distribuídos normalmente:

 #define residuals
res = model. reside

#create QQ plot
fig = sm. qqplot (res, fit= True , line=" 45 ")
plt.show() 

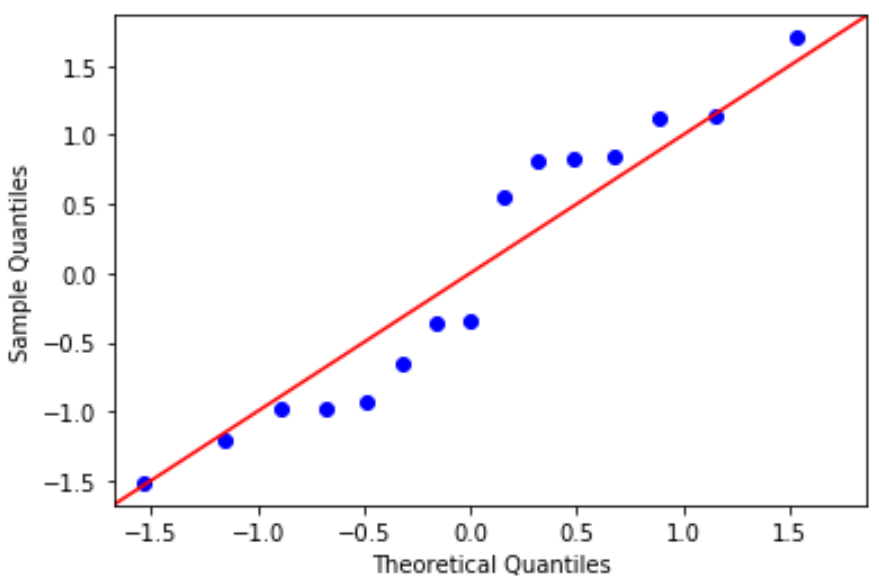
Os resíduos desviam-se um pouco da linha de 45 graus, mas não o suficiente para causar séria preocupação. Podemos assumir que a suposição de normalidade foi atendida.

Como os resíduos são normalmente distribuídos e homocedásticos, verificamos que os pressupostos do modelo de regressão linear simples são atendidos. Assim, a saída do nosso modelo é confiável.

O código Python completo usado neste tutorial pode ser encontrado aqui .