Como realizar regressão linear simples no sas

A regressão linear simples é uma técnica que podemos usar para entender a relação entre uma variável preditora e uma variável de resposta .

Esta técnica encontra a linha que melhor “se ajusta” aos dados e assume a seguinte forma:

ŷ=b ₀ + b ₁ x

Ouro:

• ŷ : O valor estimado da resposta
• b ₀ : A origem da linha de regressão
• b ₁ : A inclinação da linha de regressão

Esta equação nos ajuda a compreender a relação entre a variável preditora e a variável resposta.

O exemplo passo a passo a seguir mostra como realizar uma regressão linear simples no SAS.

Etapa 1: crie os dados

Para este exemplo, criaremos um conjunto de dados contendo o total de horas estudadas e a nota do exame final de 15 alunos.

Ajustaremos um modelo de regressão linear simples usando horas como variável preditora e pontuação como variável resposta.

O código a seguir mostra como criar este conjunto de dados no SAS:

 /*create dataset*/
data exam_data;
    input hours score;
    datalines ;
1 64
2 66
4 76
5 73
5 74
6 81
6 83
7 82
8 80
10 88
11 84
11 82
12 91
12 93
14 89
;
run ;

/*view dataset*/
proc print data =exam_data;

Etapa 2: Ajustar o modelo de regressão linear simples

A seguir, usaremos proc reg para ajustar o modelo de regressão linear simples:

 /*fit simple linear regression model*/
proc reg data =exam_data;
   model score = hours;
run ; 

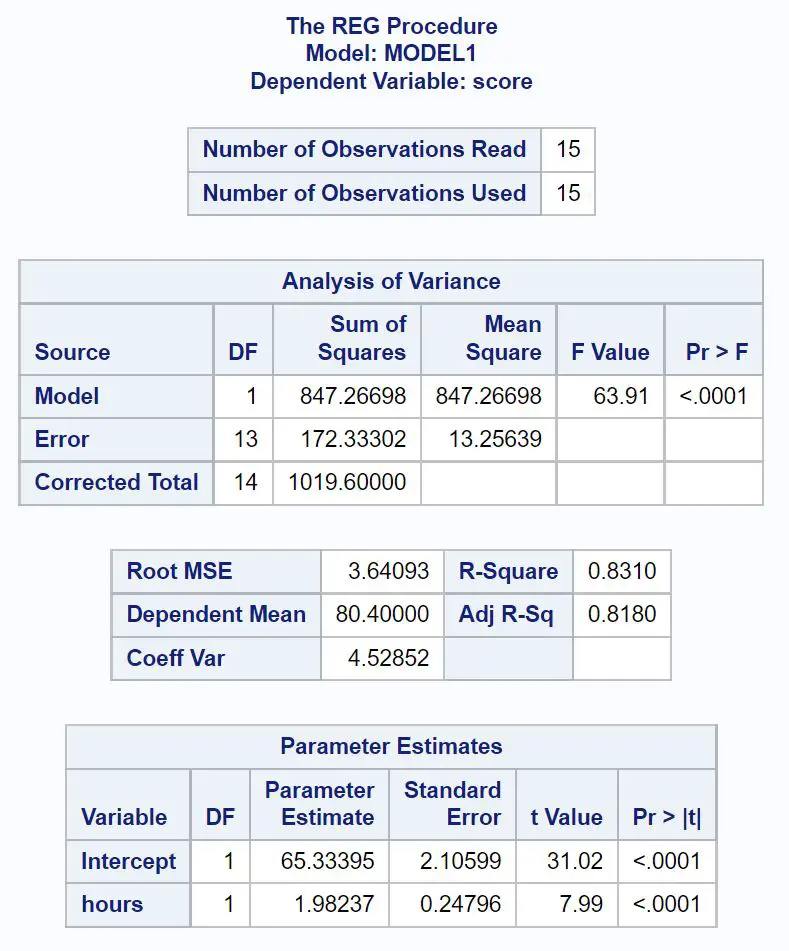
Veja como interpretar os valores mais importantes de cada tabela no resultado:

Tabela de análise de lacunas:

O valor F geral do modelo de regressão é 63,91 e o valor p correspondente é <0,0001 .

Como este valor de p é inferior a 0,05, concluímos que o modelo de regressão como um todo é estatisticamente significativo. Em outras palavras, as horas são uma variável útil para prever os resultados dos exames.

Tabela de ajuste do modelo:

O valor R-Square nos diz a porcentagem de variação nas notas dos exames que pode ser explicada pelo número de horas estudadas.

Em geral, quanto maior o valor R-quadrado de um modelo de regressão, melhores serão as variáveis preditoras em prever o valor da variável resposta.

Nesse caso, 83,1% da variação nas notas dos exames pode ser explicada pela carga horária estudada. Esse valor é bastante elevado, indicando que as horas estudadas são uma variável muito útil na previsão dos resultados dos exames.

Tabela de estimativas de parâmetros:

Nesta tabela podemos ver a equação de regressão ajustada:

Pontuação = 65,33 + 1,98*(horas)

Interpretamos isso como significando que cada hora adicional estudada está associada a um aumento médio de 1,98 pontos na nota do exame.

O valor original nos diz que a nota média do exame para um aluno que estuda zero horas é 65,33 .

Também podemos usar essa equação para encontrar a pontuação esperada no exame com base no número de horas que um aluno estuda.

Por exemplo, um aluno que estuda 10 horas deverá obter nota 85,13 no exame:

Pontuação = 65,33 + 1,98*(10) = 85,13

Como o valor p (<0,0001) para horas é inferior a 0,05 nesta tabela, concluímos que esta é uma variável preditora estatisticamente significativa.

Passo 3: Analisar gráficos residuais

A regressão linear simples faz duas suposições importantes sobre os resíduos do modelo:

• Os resíduos são normalmente distribuídos.
• Os resíduos possuem variância igual (“ homocedasticidade ”) em cada nível da variável preditora.

Se estes pressupostos não forem cumpridos, os resultados do nosso modelo de regressão poderão não ser fiáveis.

Para verificar se essas suposições foram atendidas, podemos analisar os gráficos residuais que o SAS exibe automaticamente na saída:

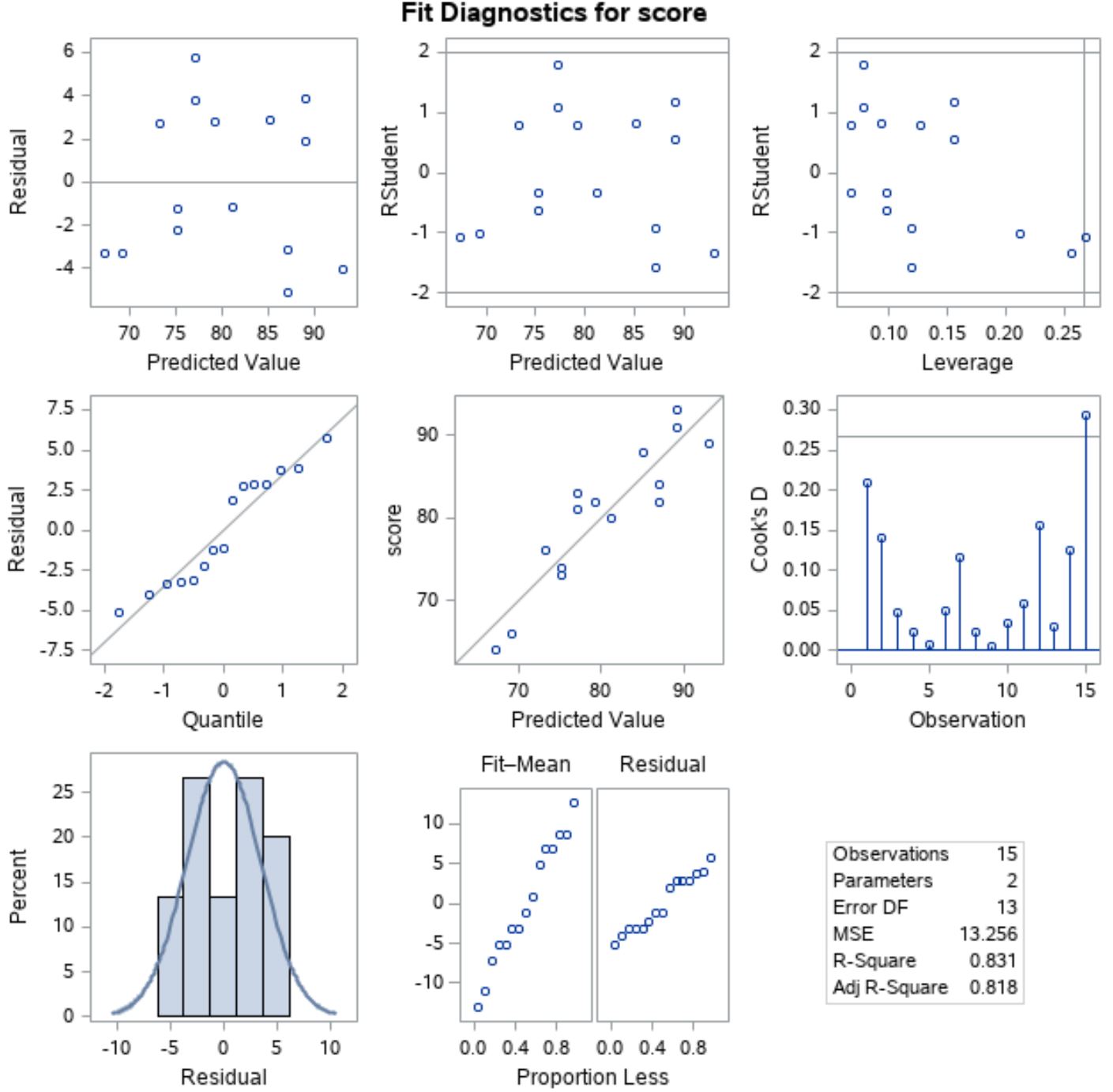
Para verificar se os resíduos estão normalmente distribuídos , podemos analisar o gráfico na posição esquerda da linha média com “Quantil” ao longo do eixo x e “Residual” ao longo do eixo y.

Este gráfico é chamado de gráfico QQ , abreviação de “quantil-quantil”, e é usado para determinar se os dados são normalmente distribuídos ou não. Se os dados forem distribuídos normalmente, os pontos em um gráfico QQ estarão em uma linha reta diagonal.

No gráfico podemos ver que os pontos estão aproximadamente ao longo de uma linha reta diagonal, então podemos assumir que os resíduos são normalmente distribuídos.

A seguir, para verificar se os resíduos são homocedásticos , podemos observar o gráfico na posição esquerda da primeira linha com “Valor previsto” ao longo do eixo xe “Residual” ao longo do eixo y.

Se os pontos do gráfico estiverem espalhados aleatoriamente em torno de zero sem um padrão claro, então podemos assumir que os resíduos são homocedásticos.

No gráfico podemos ver que os pontos estão espalhados em torno de zero aleatoriamente com variância aproximadamente igual em cada nível ao longo do gráfico, portanto podemos assumir que os resíduos são homocedásticos.

Uma vez que ambos os pressupostos são atendidos, podemos assumir que os resultados do modelo de regressão linear simples são confiáveis.

Recursos adicionais

Os tutoriais a seguir explicam como executar outras tarefas comuns no SAS:

Como realizar ANOVA unidirecional no SAS
Como realizar ANOVA bidirecional no SAS
Como calcular a correlação no SAS