Como realizar regressão logística no sas
A regressão logística é um método que podemos usar para ajustar um modelo de regressão quando a variável de resposta é binária.
A regressão logística usa um método conhecido como estimativa de máxima verossimilhança para encontrar uma equação da seguinte forma:
log[p(X) / (1 – p(X))] = β 0 + β 1 X 1 + β 2 X 2 +… + β p
Ouro:
- X j : a j- ésima variável preditiva
- β j : estimativa do coeficiente para a j -ésima variável preditiva
A fórmula no lado direito da equação prevê o log de probabilidade de que a variável de resposta assuma o valor 1.
O exemplo passo a passo a seguir mostra como ajustar um modelo de regressão logística no SAS.
Etapa 1: crie o conjunto de dados
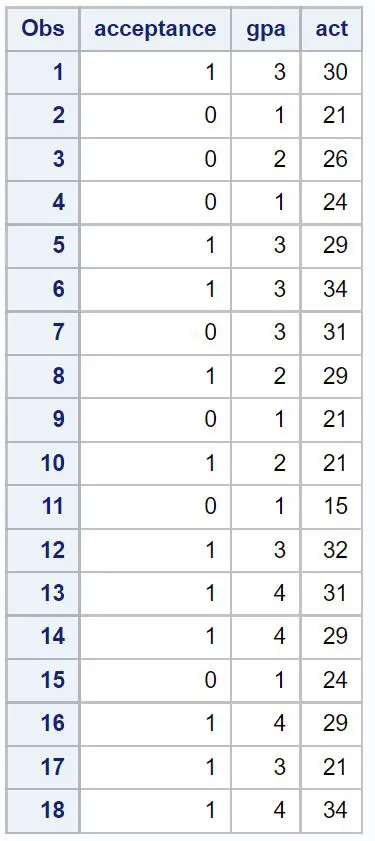
Primeiro, criaremos um conjunto de dados contendo informações sobre as três variáveis a seguir para 18 alunos:
- Aceitação em determinada faculdade (1 = sim, 0 = não)
- GPA (escala de 1 a 4)
- Pontuação ACT (escala de 1 a 36)
/*create dataset*/ data my_data; input acceptance gpa act; datalines ; 1 3 30 0 1 21 0 2 26 0 1 24 1 3 29 1 3 34 0 3 31 1 2 29 0 1 21 1 2 21 0 1 15 1 3 32 1 4 31 1 4 29 0 1 24 1 4 29 1 3 21 1 4 34 ; run ; /*view dataset*/ proc print data =my_data;
Passo 2: Ajustar o modelo de regressão logística
A seguir, usaremos proc Logistics para ajustar o modelo de regressão logística, usando “aceitação” como variável de resposta e “gpa” e “agir” como variáveis preditoras.
Nota : A diminuição deve ser especificada para o SAS prever a probabilidade de a variável de resposta assumir o valor 1. Por padrão, o SAS prevê a probabilidade de a variável de resposta assumir o valor 0.
/*fit logistic regression model*/
proc logistic data =my_data descending ;
model acceptance = gpa act;
run ;
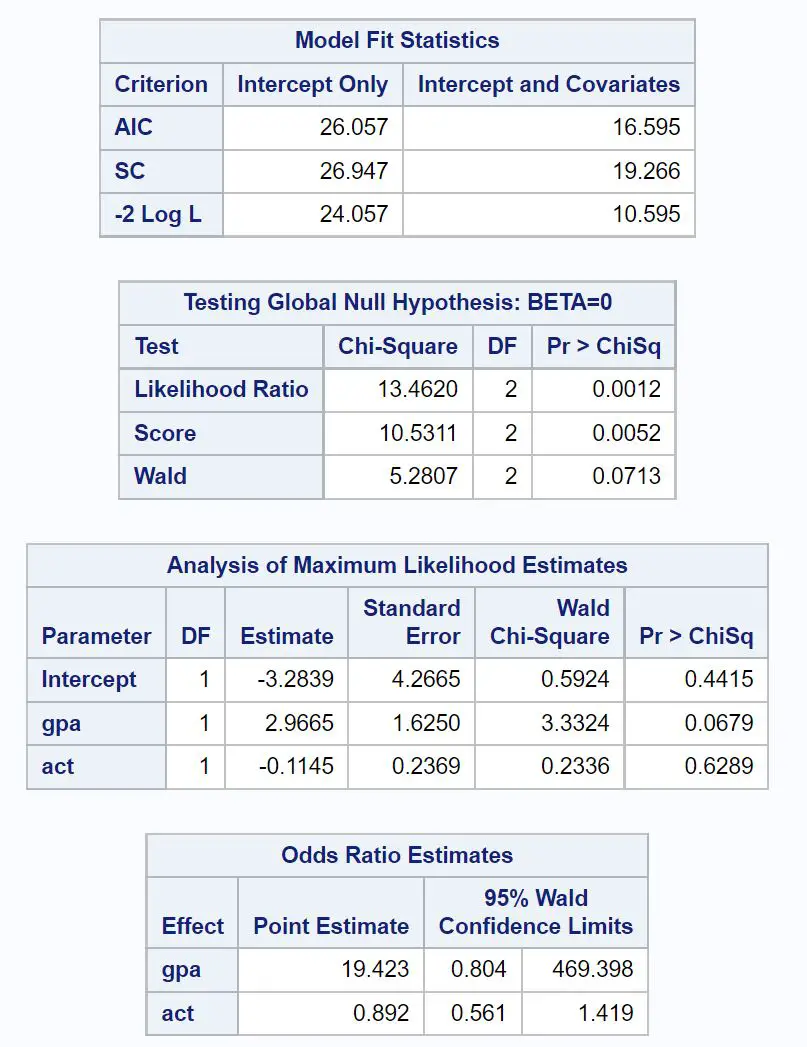
A primeira tabela de interesse é intitulada Model Fit Statistics .
Nesta tabela podemos ver o valor AIC do modelo, que é 16.595 . Quanto menor o valor do AIC, melhor o modelo é capaz de ajustar os dados.
No entanto, não há limite para o que é considerado um valor “bom” de AIC . Em vez disso, usamos o AIC para comparar o ajuste de vários modelos ao mesmo conjunto de dados. O modelo com o menor valor de AIC é geralmente considerado o melhor.
A próxima tabela de interesse é intitulada Testando a hipótese nula global: BETA=0 .
Nesta tabela, podemos ver o valor qui-quadrado da razão de verossimilhança de 13,4620 com um valor p correspondente de 0,0012 .
Como esse valor p é inferior a 0,05, isso nos diz que o modelo de regressão logística como um todo é estatisticamente significativo.
A seguir, podemos analisar as estimativas dos coeficientes na tabela intitulada Análise de estimativas de máxima verossimilhança .
Nesta tabela podemos ver os coeficientes de gpa e act, que indicam a variação média no logaritmo das chances de ser aceito na faculdade para um aumento de uma unidade em cada variável.
Por exemplo:
- Um aumento de uma unidade no valor do GPA está associado a um aumento médio de 2,9665 nas chances logarítmicas de ser aceito na faculdade.
- Um aumento de uma unidade na pontuação do ACT está associado a uma diminuição média de 0,1145 nas chances logarítmicas de ser aceito na faculdade.
Os valores p correspondentes no resultado também nos dão uma ideia de quão eficaz é cada variável preditora em prever a probabilidade de ser aceita:
- Valor P do GPA: 0,0679
- Valor ACT P: 0,6289
Isto nos diz que o GPA parece ser um preditor estatisticamente significativo de aceitação na faculdade, enquanto a pontuação do ACT não parece ser estatisticamente significativa.
Recursos adicionais
Os tutoriais a seguir explicam como ajustar outros modelos de regressão no SAS:
Como realizar regressão linear simples no SAS
Como realizar regressão linear múltipla no SAS