Regressão polinomial

Este artigo explica o que é regressão polinomial em estatística e como ela é executada. Além disso, você poderá ver um exemplo em que é realizada uma regressão polinomial.

O que é regressão polinomial?

Regressão polinomial , ou regressão polinomial , é um modelo de regressão em que a relação entre a variável independente X e a variável dependente Y é modelada usando um polinômio.

Por exemplo, a equação para um modelo de regressão polinomial quadrática é y=β ₀ +β ₁ x+β ₂ x ² +ε.

A regressão polinomial é útil para ajustar conjuntos de dados cujos gráficos são curvas polinomiais. Portanto, se o gráfico de pontos de uma amostra de dados tiver o formato de uma parábola, será melhor construir um modelo de regressão quadrática em vez de um modelo de regressão linear. Dessa forma, a equação do modelo de regressão se ajustará melhor à amostra de dados.

Observe que a regressão polinomial é um tipo de regressão não linear, assim como a regressão exponencial e a regressão logarítmica.

Fórmula de regressão polinomial

A equação para um modelo de regressão polinomial é y=β ₀ +β ₁ x+β ₂ x ² +β ₃ x ³ …+β _m x ^m +ε.

Ouro:

• 

  é a variável dependente.

• 

  é a variável independente.

• 

  é a constante da equação de regressão polinomial.

• 

  é o coeficiente de regressão associado à variável

  

  .

• 

  Este é o erro ou resíduo, ou seja, a diferença entre o valor observado e o valor estimado pelo modelo.

Então, se tivermos uma amostra com um total de

observações, podemos propor o modelo de regressão polinomial em forma de matriz:

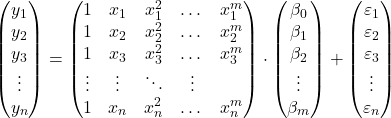
A expressão matricial acima pode ser reescrita atribuindo uma letra a cada matriz:

Assim, aplicando o critério dos mínimos quadrados , podemos chegar à fórmula para estimar os coeficientes de um modelo de regressão polinomial :

Porém, fazer esses cálculos manualmente é muito trabalhoso e demorado, por isso é mais conveniente usar softwares de computador (como Minitab ou Excel) que permitem realizar um modelo de regressão polinomial com muito mais rapidez.

Exemplo de modelo de regressão polinomial

Agora que sabemos a definição de regressão polinomial e como ela é realizada, vejamos um exemplo da vida real para compreender totalmente o conceito.

Em primeiro lugar, deve-se ter em mente que um modelo de regressão polinomial deve ser realizado quando o gráfico de dados tiver o formato de uma curva polinomial. Por exemplo, se o gráfico de pontos estiver na forma de uma curva cúbica, precisamos construir um modelo de regressão polinomial de terceiro grau.

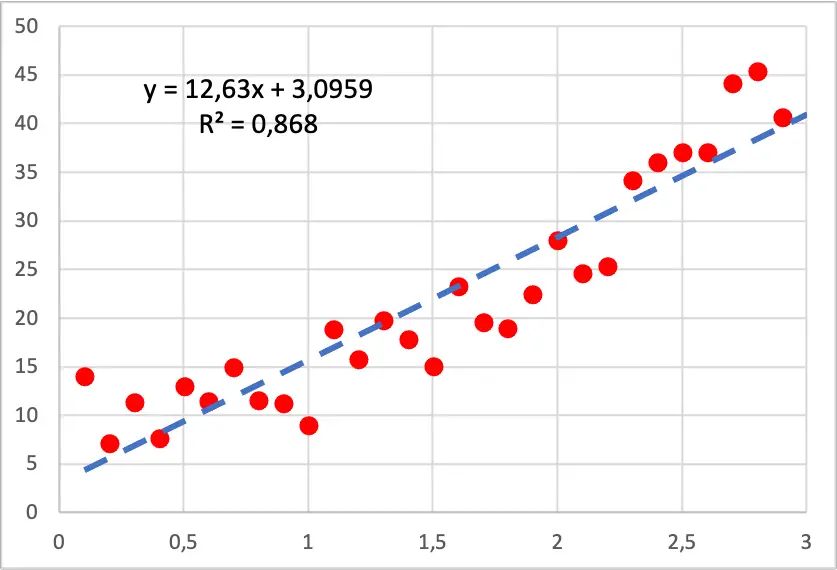
Então, como você pode ver na imagem a seguir, o gráfico de pontos dos nossos dados tem um formato quadrático, pois à medida que aumentamos o valor da variável independente, a variável dependente cresce mais rápido. Neste caso foi realizado um modelo de regressão linear e como você pode ver ele não se ajusta bem aos pontos porque possui seções em que a linha está abaixo de todos os pontos e seções em que a linha está acima deles.

Por outro lado, se executarmos um modelo de regressão polinomial quadrática, ele se ajusta muito melhor aos dados amostrais, como você pode ver na imagem abaixo.

Além disso, ao desenvolver um modelo de regressão polinomial, o coeficiente de determinação melhora consideravelmente, pois passa de 86,80% para 94,05%. Portanto, o novo modelo de regressão explica muito melhor o conjunto de dados.

Por outro lado, outra indicação de que precisamos realizar a regressão polinomial é a plotagem dos resíduos. Se numa regressão linear o gráfico dos resíduos tem o formato de uma parábola ou outro tipo de polinômio, um modelo de regressão polinomial certamente se ajusta melhor aos dados estudados.

Outros tipos de regressão não linear

Existem principalmente três tipos de regressão não linear:

• Regressão Polinomial – A equação do modelo de regressão está na forma de um polinômio.
• Regressão logarítmica : é obtido o logaritmo da variável independente.
• Regressão Exponencial : A variável independente é encontrada no expoente da equação.