Regressão polinomial em r (passo a passo)

A regressão polinomial é uma técnica que podemos usar quando o relacionamento entre uma variável preditora e uma variável de resposta é não linear.

Este tipo de regressão assume a forma:

Y = β ₀ ⁺ β ₁ X + β ₂ X ² +… + β _h

onde h é o “grau” do polinômio.

Este tutorial fornece um exemplo passo a passo de como realizar regressão polinomial em R.

Etapa 1: crie os dados

Para este exemplo, criaremos um conjunto de dados contendo a quantidade de horas estudadas e a nota do exame final para uma turma de 50 alunos:

 #make this example reproducible
set.seed(1)

#create dataset
df <- data.frame(hours = runif (50, 5, 15), score=50)
df$score = df$score + df$hours^3/150 + df$hours* runif (50, 1, 2)

#view first six rows of data
head(data)

      hours score
1 7.655087 64.30191
2 8.721239 70.65430
3 10.728534 73.66114
4 14.082078 86.14630
5 7.016819 59.81595
6 13.983897 83.60510

Etapa 2: visualize os dados

Antes de ajustar um modelo de regressão aos dados, vamos primeiro criar um gráfico de dispersão para visualizar a relação entre horas estudadas e nota no exame:

 library (ggplot2)

ggplot(df, aes (x=hours, y=score)) +
  geom_point() 

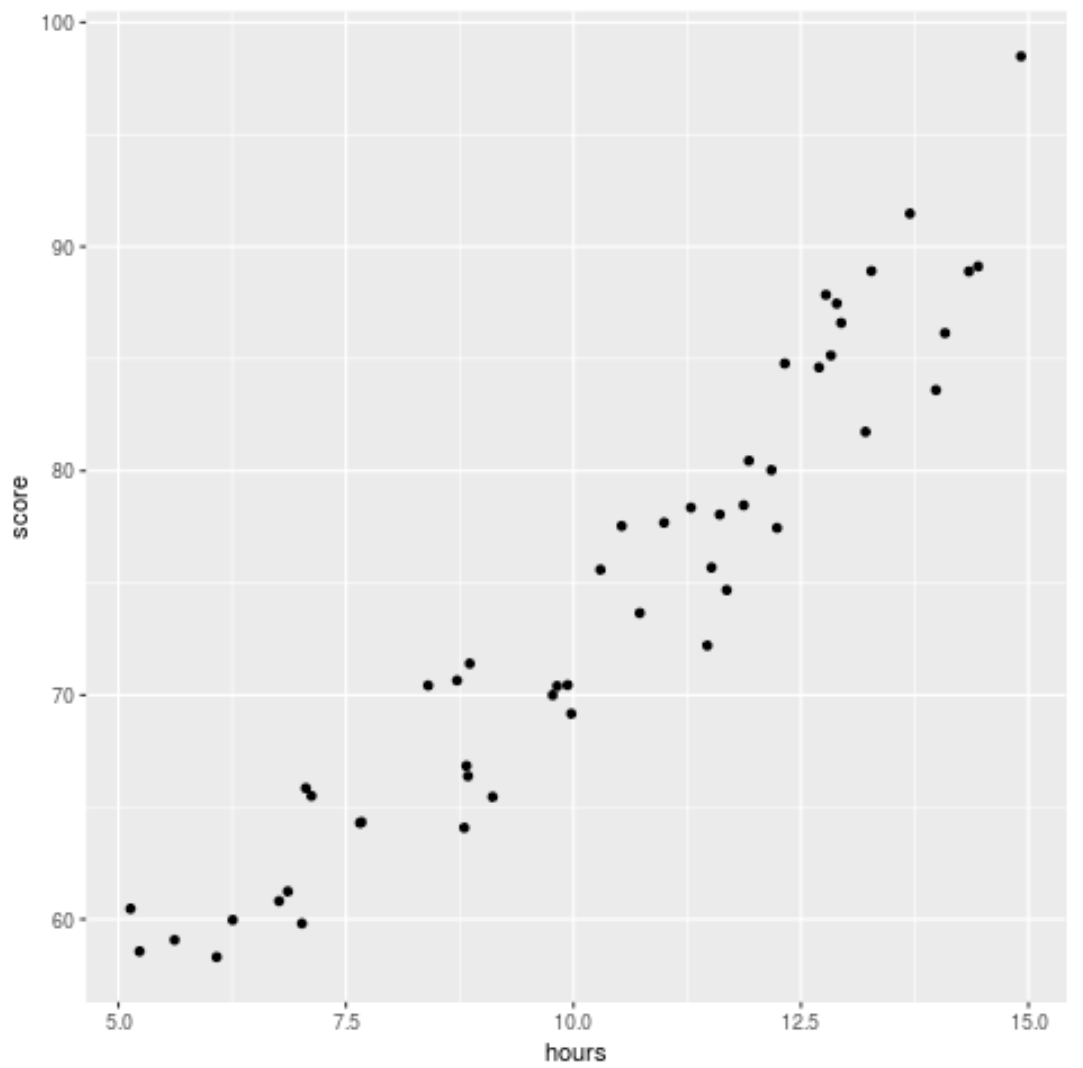
Podemos ver que os dados têm uma relação ligeiramente quadrática, indicando que a regressão polinomial pode se ajustar melhor aos dados do que a regressão linear simples.

Etapa 3: Ajustar modelos de regressão polinomial

A seguir, ajustaremos cinco modelos de regressão polinomial diferentes com graus h = 1…5 e usaremos a validação cruzada k-fold com k = 10 vezes para calcular o teste MSE para cada modelo:

 #randomly shuffle data
df.shuffled <- df[ sample ( nrow (df)),]

#define number of folds to use for k-fold cross-validation
K <- 10 

#define degree of polynomials to fit
degree <- 5

#create k equal-sized folds
folds <- cut( seq (1, nrow (df.shuffled)), breaks=K, labels= FALSE )

#create object to hold MSE's of models
mse = matrix(data=NA,nrow=K,ncol=degree)

#Perform K-fold cross validation
for (i in 1:K){
    
#define training and testing data
testIndexes <- which (folds==i,arr.ind= TRUE )
    testData <- df.shuffled[testIndexes, ]
    trainData <- df.shuffled[-testIndexes, ]
    
#use k-fold cv to evaluate models
for (j in 1:degree){
        fit.train = lm (score ~ poly (hours,d), data=trainData)
        fit.test = predict (fit.train, newdata=testData)
        mse[i,j] = mean ((fit.test-testData$score)^2) 
    }
}

#find MSE for each degree 
colMeans(mse)

[1] 9.802397 8.748666 9.601865 10.592569 13.545547

Pelo resultado podemos ver o teste MSE para cada modelo:

• Teste MSE com grau h = 1: 9,80
• Teste MSE com grau h = 2: 8,75
• Teste MSE com grau h = 3: 9,60
• Teste MSE com grau h = 4: 10,59
• Teste MSE com grau h = 5: 13,55

O modelo com menor MSE de teste acabou sendo o modelo de regressão polinomial com grau h = 2.

Isso corresponde à nossa intuição do gráfico de dispersão original: um modelo de regressão quadrática melhor se ajusta aos dados.

Passo 4: Analise o modelo final

Finalmente, podemos obter os coeficientes do modelo com melhor desempenho:

 #fit best model
best = lm (score ~ poly (hours,2, raw= T ), data=df)

#view summary of best model
summary(best)

Call:
lm(formula = score ~ poly(hours, 2, raw = T), data = df)

Residuals:
    Min 1Q Median 3Q Max 
-5.6589 -2.0770 -0.4599 2.5923 4.5122 

Coefficients:
                         Estimate Std. Error t value Pr(>|t|)    
(Intercept) 54.00526 5.52855 9.768 6.78e-13 ***
poly(hours, 2, raw = T)1 -0.07904 1.15413 -0.068 0.94569    
poly(hours, 2, raw = T)2 0.18596 0.05724 3.249 0.00214 ** 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

A partir do resultado, podemos ver que o modelo final ajustado é:

Pontuação = 54,00526 – 0,07904*(horas) + 0,18596*(horas) ²

Podemos usar esta equação para estimar a pontuação que um aluno receberá com base no número de horas estudadas.

Por exemplo, um aluno que estuda 10 horas deverá obter nota 71,81 :

Pontuação = 54,00526 – 0,07904*(10) + 0,18596*(10) ² = 71,81

Também podemos traçar o modelo ajustado para ver quão bem ele se ajusta aos dados brutos:

 ggplot(df, aes (x=hours, y=score)) + 
          geom_point() +
          stat_smooth(method=' lm ', formula = y ~ poly (x,2), size = 1) + 
          xlab(' Hours Studied ') +
          ylab(' Score ') 

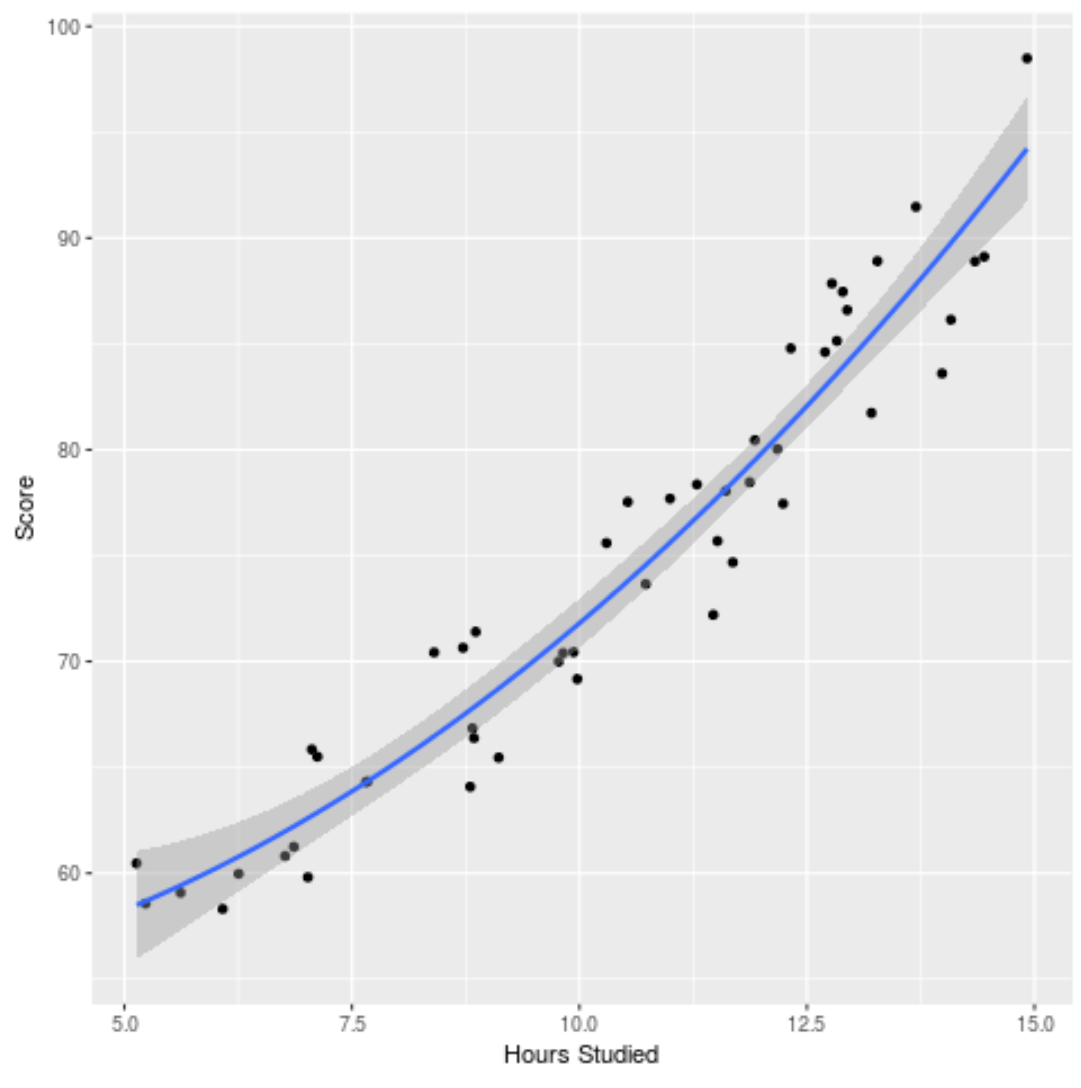
Você pode encontrar o código R completo usado neste exemplo aqui .