Como realizar regressão quadrática em r

Quando duas variáveis têm uma relação linear, muitas vezes podemos usar a regressão linear simples para quantificar a sua relação.

No entanto, quando duas variáveis têm uma relação quadrática, podemos usar a regressão quadrática para quantificar a sua relação.

Este tutorial explica como realizar regressão quadrática em R.

Exemplo: regressão quadrática em R

Suponha que queiramos compreender a relação entre o número de horas trabalhadas e a felicidade relatada. Temos os seguintes dados sobre o número de horas trabalhadas por semana e o nível de felicidade relatado (numa escala de 0 a 100) para 11 pessoas diferentes:

Use as etapas a seguir para ajustar um modelo de regressão quadrática em R.

Passo 1: Insira os dados.

Primeiro, criaremos um data frame contendo nossos dados:

 #createdata
data <- data.frame(hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60),
                   happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27))

#viewdata 
data

   hours happiness
1 6 14
2 9 28
3 12 50
4 14 70
5 30 89
6 35 94
7 40 90
8 47 75
9 51 59
10 55 44
11 60 27

Etapa 2: visualize os dados.

A seguir, criaremos um gráfico de dispersão simples para visualizar os dados.

 #create scatterplot
plot(data$hours, data$happiness, pch=16) 

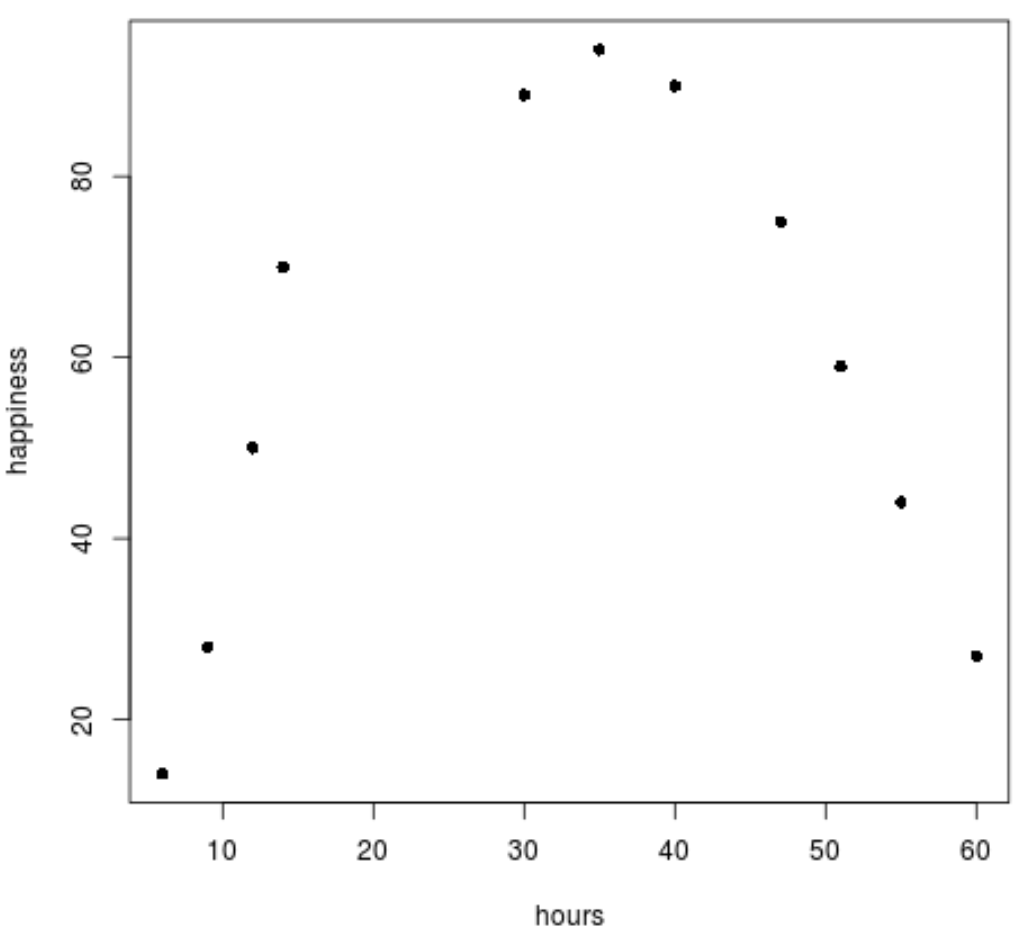
Podemos ver claramente que os dados não seguem um padrão linear.

Etapa 3: ajuste um modelo de regressão linear simples.

A seguir, ajustaremos um modelo de regressão linear simples para ver quão bem ele se ajusta aos dados:

 #fit linear model
linearModel <- lm(happiness ~ hours, data=data)

#view model summary
summary(linearModel)

Call:
lm(formula = happiness ~ hours)

Residuals:
   Min 1Q Median 3Q Max 
-39.34 -21.99 -2.03 23.50 35.11 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)  
(Intercept) 48.4531 17.3288 2.796 0.0208 *
hours 0.2981 0.4599 0.648 0.5331  
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 28.72 on 9 degrees of freedom
Multiple R-squared: 0.0446, Adjusted R-squared: -0.06156 
F-statistic: 0.4201 on 1 and 9 DF, p-value: 0.5331

A variância total na felicidade explicada pelo modelo é de apenas 4,46% , conforme mostrado pelo valor múltiplo de R ao quadrado.

Etapa 4: ajuste um modelo de regressão quadrática.

A seguir, ajustaremos um modelo de regressão quadrática.

 #create a new variable for hours 2
data$hours2 <- data$hours^2

#fit quadratic regression model
quadraticModel <- lm(happiness ~ hours + hours2, data=data)

#view model summary
summary(quadraticModel)

Call:
lm(formula = happiness ~ hours + hours2, data = data)

Residuals:
    Min 1Q Median 3Q Max 
-6.2484 -3.7429 -0.1812 1.1464 13.6678 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -18.25364 6.18507 -2.951 0.0184 *  
hours 6.74436 0.48551 13.891 6.98e-07 ***
hours2 -0.10120 0.00746 -13.565 8.38e-07 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 6.218 on 8 degrees of freedom
Multiple R-squared: 0.9602, Adjusted R-squared: 0.9502 
F-statistic: 96.49 on 2 and 8 DF, p-value: 2.51e-06

A variância total da felicidade explicada pelo modelo aumentou para 96,02% .

Podemos usar o código a seguir para visualizar quão bem o modelo se ajusta aos dados:

 #create sequence of hour values
hourValues <- seq(0, 60, 0.1)

#create list of predicted happiness levels using quadratic model
happinessPredict <- predict(quadraticModel, list(hours=hourValues, hours2=hourValues^2))

#create scatterplot of original data values
plot(data$hours, data$happiness, pch=16)
#add predicted lines based on quadratic regression model
lines(hourValues, happinessPredict, col='blue')

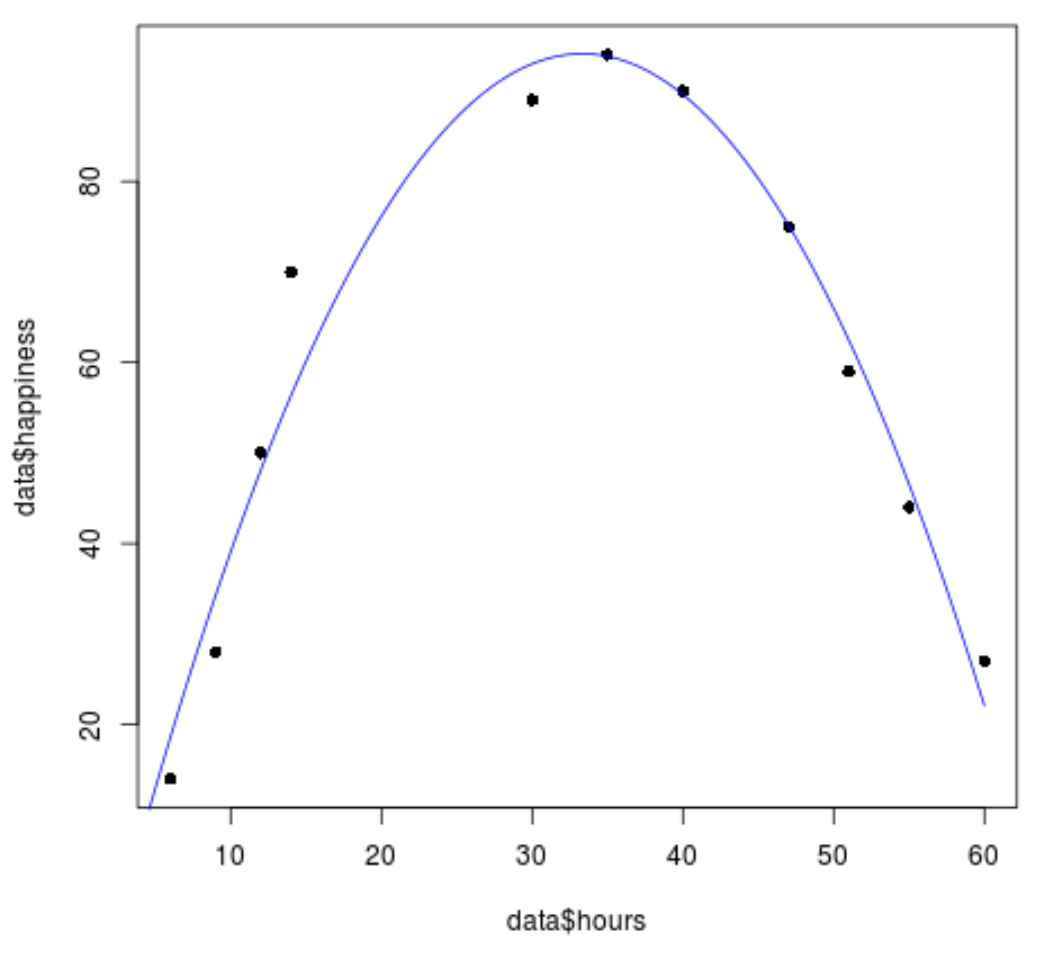
Podemos ver que a linha de regressão quadrática se ajusta muito bem aos valores dos dados.

Etapa 5: Interprete o modelo de regressão quadrática.

Na etapa anterior, vimos que o resultado do modelo de regressão quadrática foi:

 Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -18.25364 6.18507 -2.951 0.0184 *  
hours 6.74436 0.48551 13.891 6.98e-07 ***
hours2 -0.10120 0.00746 -13.565 8.38e-07 ***

Com base nos coeficientes aqui apresentados, a regressão quadrática ajustada seria:

Felicidade = -0,1012 (horas) ² + 6,7444 (horas) – 18,2536

Podemos utilizar esta equação para determinar a felicidade prevista de um indivíduo, dado o número de horas que trabalha por semana.

Por exemplo, uma pessoa que trabalha 60 horas por semana teria um nível de felicidade de 22,09 :

Felicidade = -0,1012(60) ² + 6,7444(60) – 18,2536 = 22,09

Por outro lado, uma pessoa que trabalha 30 horas por semana deveria ter um nível de felicidade de 92,99 :

Felicidade = -0,1012(30) ² + 6,7444(30) – 18,2536 = 92,99