Como realizar regressão quadrática no spss

Quando duas variáveis têm um relacionamento linear, muitas vezes você pode usar a regressão linear simples para quantificar seu relacionamento.

No entanto, a regressão linear simples não funciona bem quando duas variáveis têm uma relação não linear. Nestes casos, você pode tentar usar a regressão quadrática .

Este tutorial explica como realizar regressão quadrática no SPSS.

Exemplo: Regressão Quadrática no SPSS

Suponha que queiramos compreender a relação entre o número de horas trabalhadas e a felicidade. Temos os seguintes dados sobre o número de horas trabalhadas por semana e o nível de felicidade relatado (numa escala de 0 a 100) para 16 pessoas diferentes:

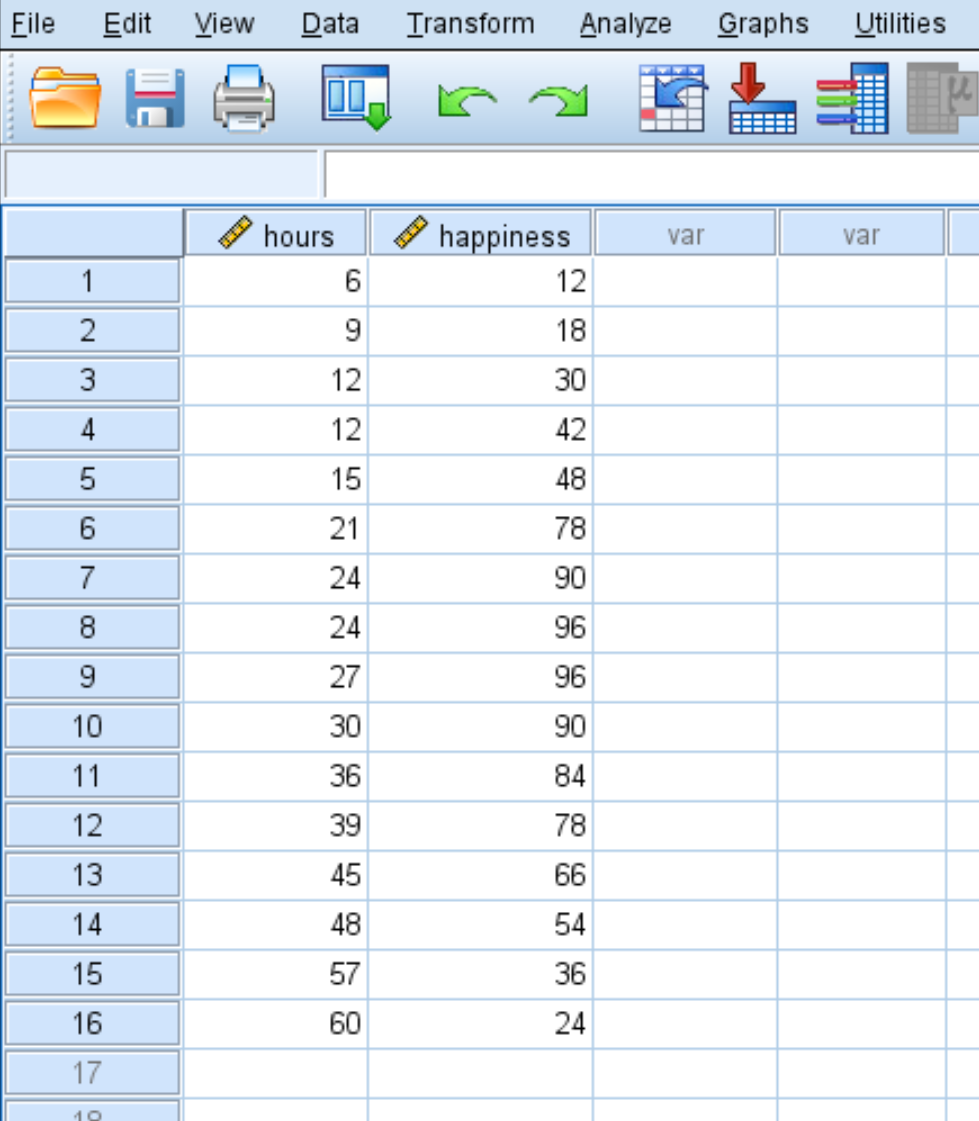
Use as etapas a seguir para realizar a regressão quadrática no SPSS.

Etapa 1: visualize os dados.

Antes de realizar uma regressão quadrática, vamos criar um gráfico de dispersão para visualizar a relação entre horas trabalhadas e felicidade para verificar se as duas variáveis realmente possuem uma relação quadrática.

Clique na guia Gráficos e em Construtor de Gráficos :

Na nova janela que aparece, escolha Dispersão/Ponto na lista Escolher . Em seguida, arraste o gráfico denominado Simple Scatter para a janela principal de edição. Arraste horas variáveis no eixo x e felicidade no eixo y. Em seguida, clique em OK .

O seguinte gráfico de dispersão aparecerá:

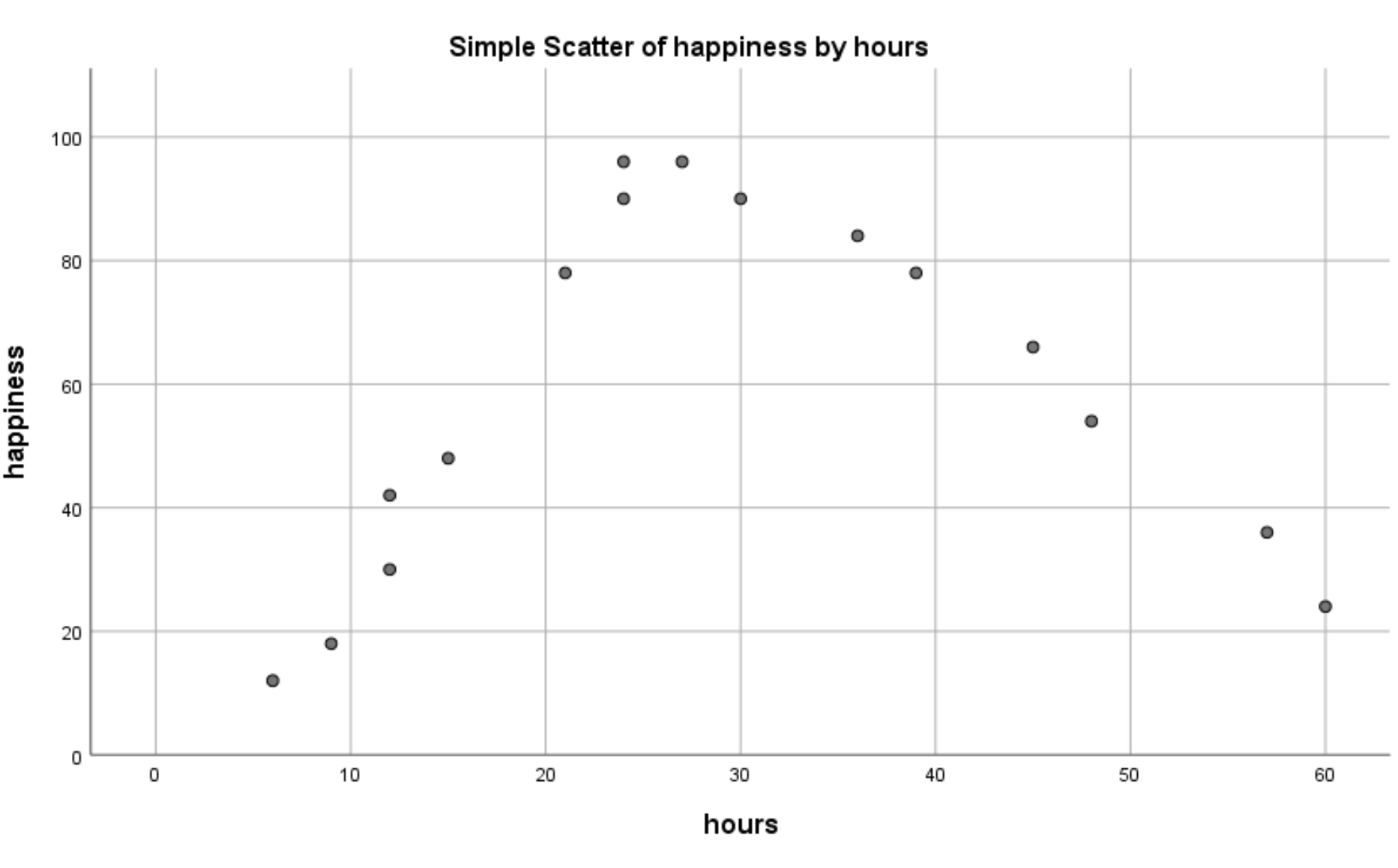
Podemos ver claramente que existe uma relação não linear entre horas trabalhadas e felicidade. Isso nos diz que a regressão quadrática é uma técnica apropriada para usar nesta situação.

Etapa 2: Crie uma nova variável.

Antes de podermos realizar uma regressão quadrática, precisamos criar uma variável preditora para horas ² .

Clique na guia Transformação e em Calcular Variável :

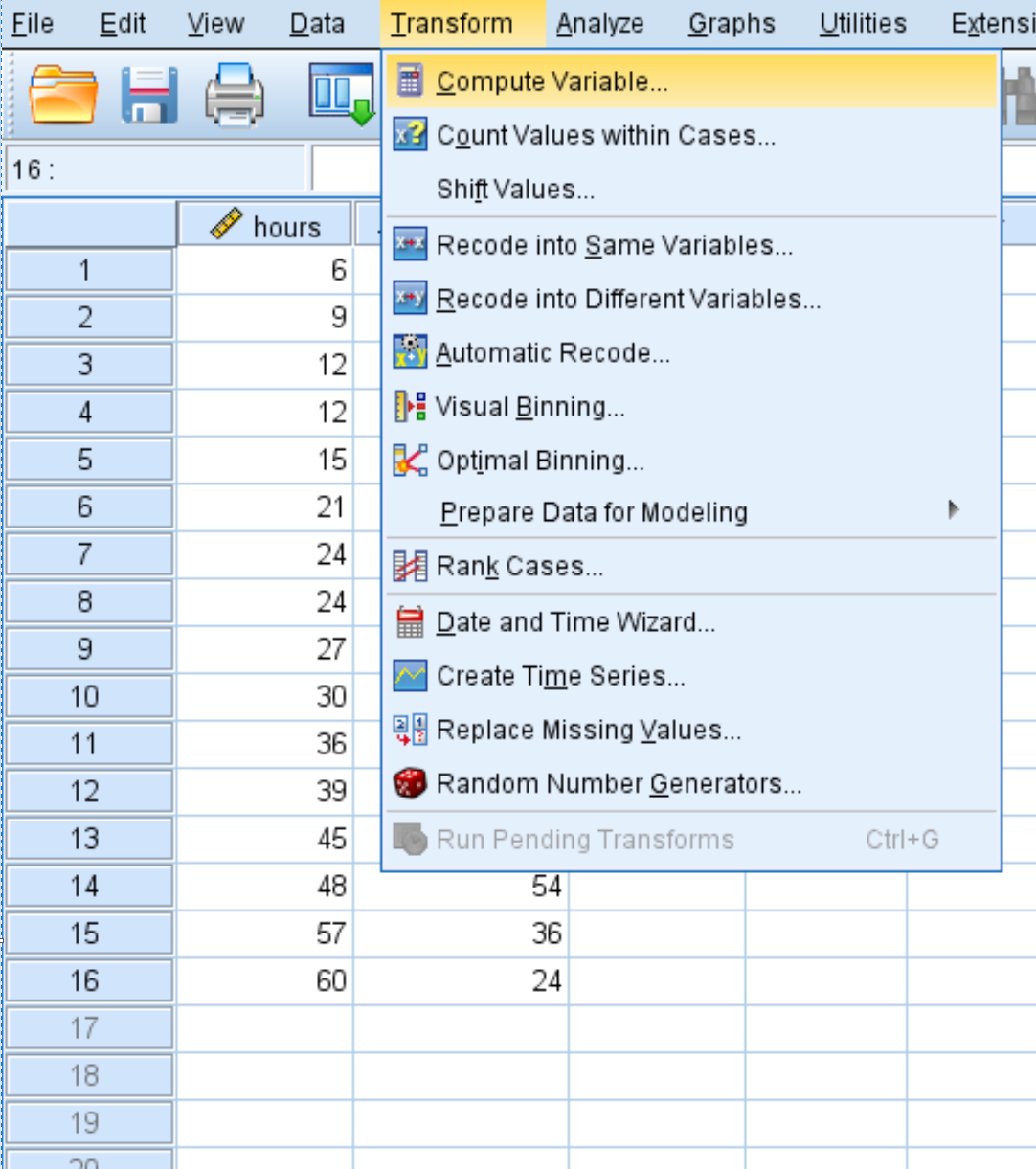
Na nova janela que aparece, nomeie a variável de destino hours2 e defina-a como hours*hours :

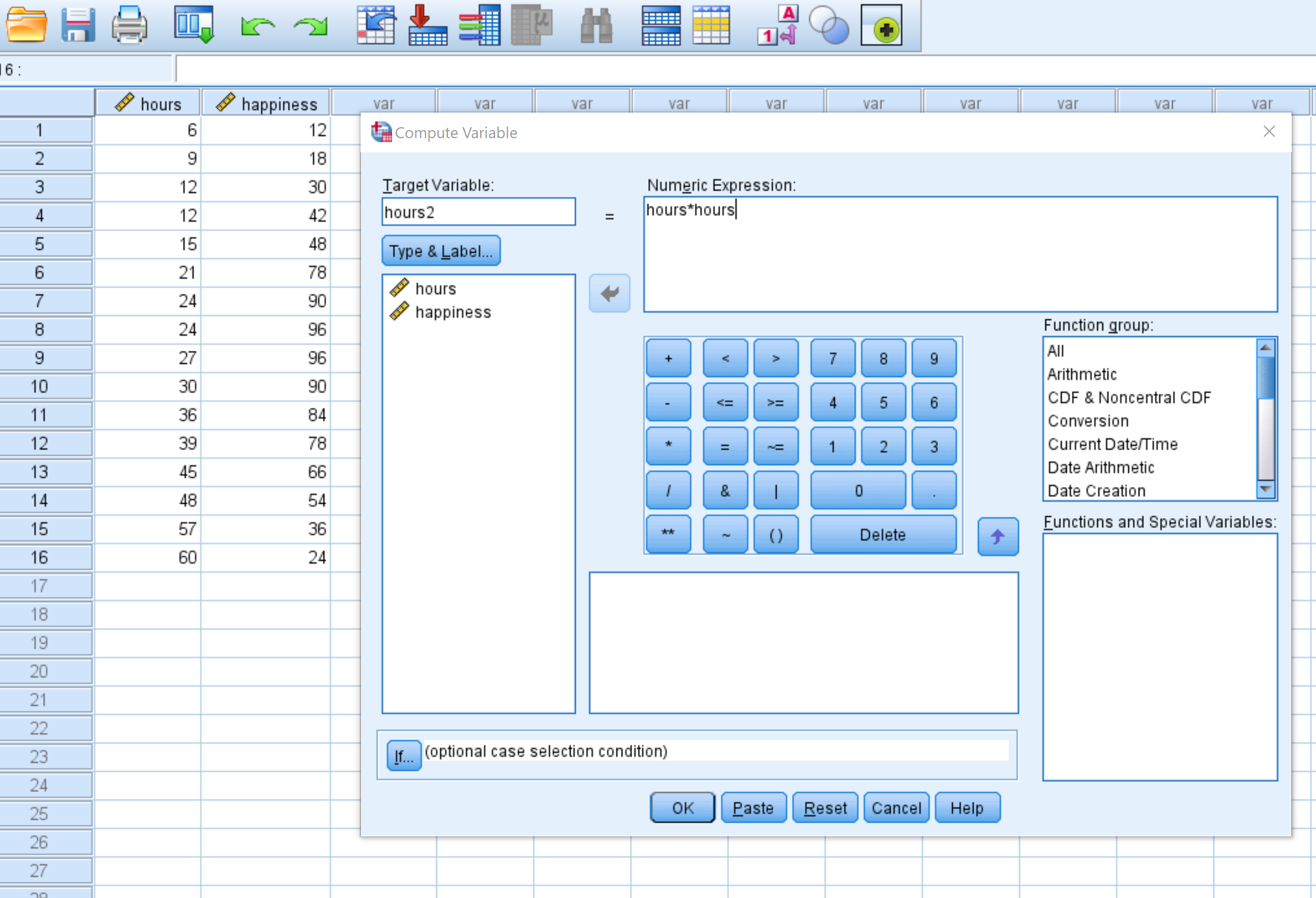
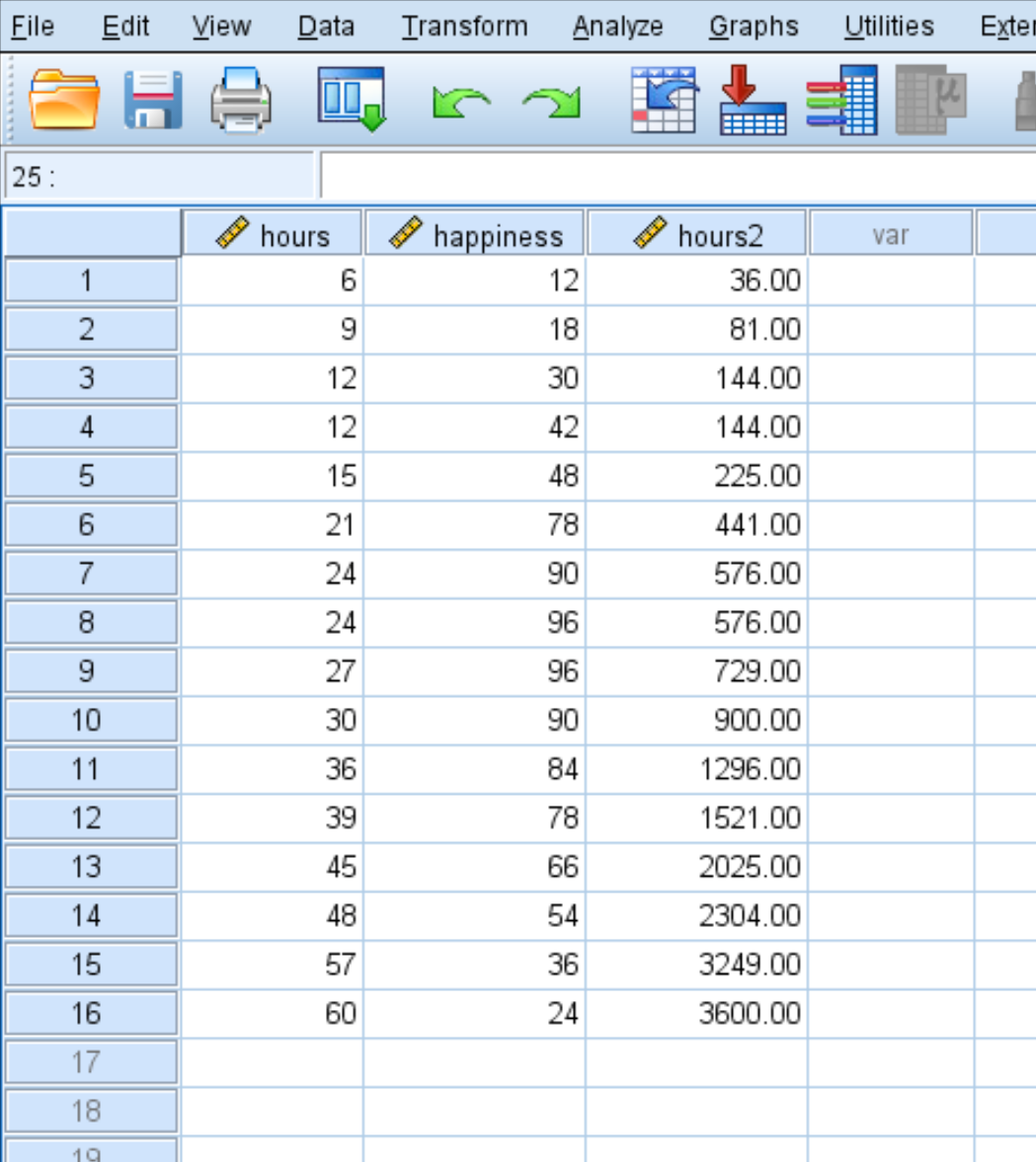
Depois de clicar em OK , a variável hours2 aparecerá em uma nova coluna:

Etapa 3: execute a regressão quadrática.

A seguir, realizaremos uma regressão quadrática. Clique na guia Analisar , depois em Regressão e depois em Linear :

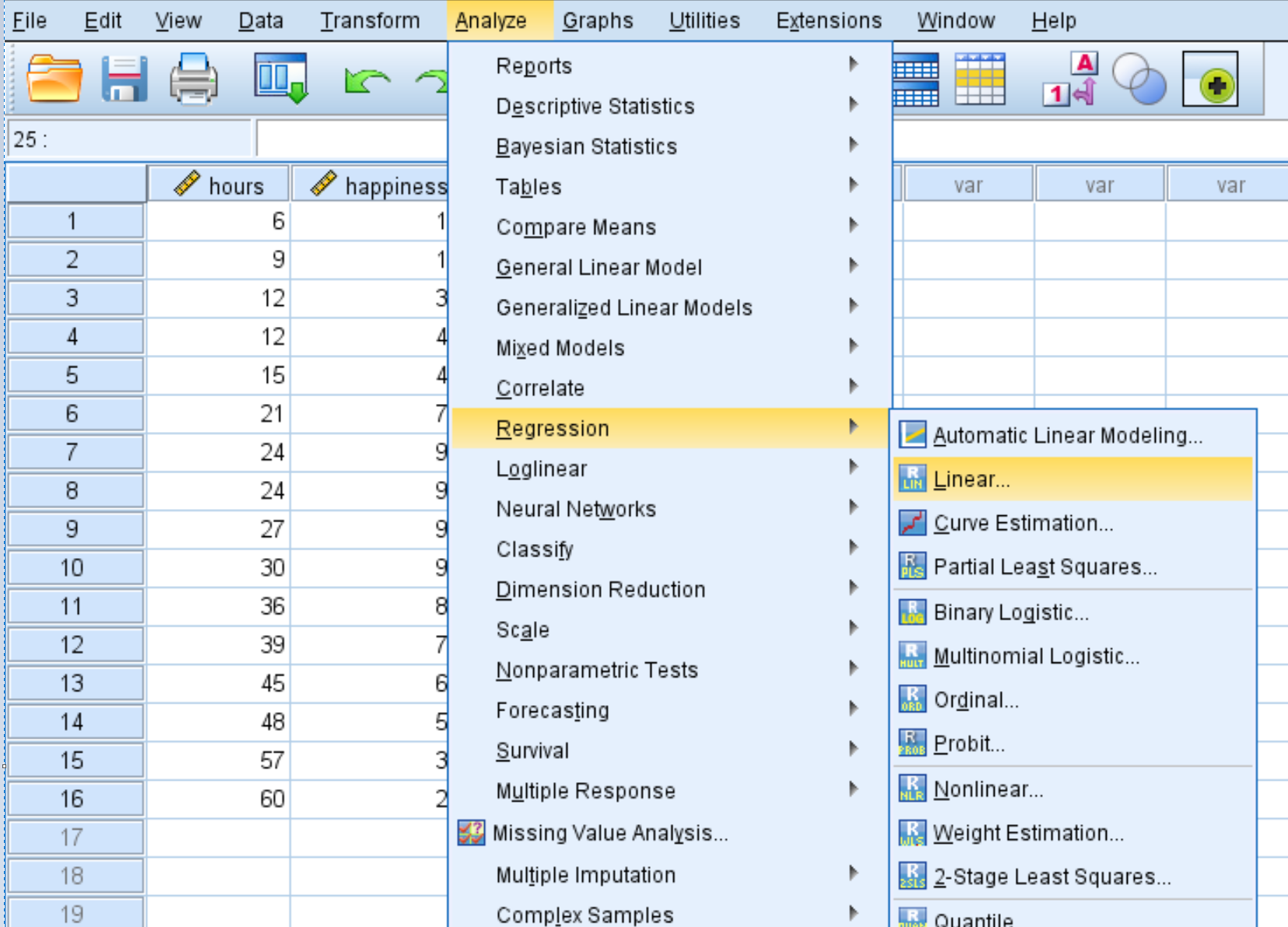
Na nova janela que aparece, arraste a felicidade para a caixa denominada Dependente. Arraste Horas e Horas2 para a caixa denominada Independente(s). Em seguida, clique em OK .

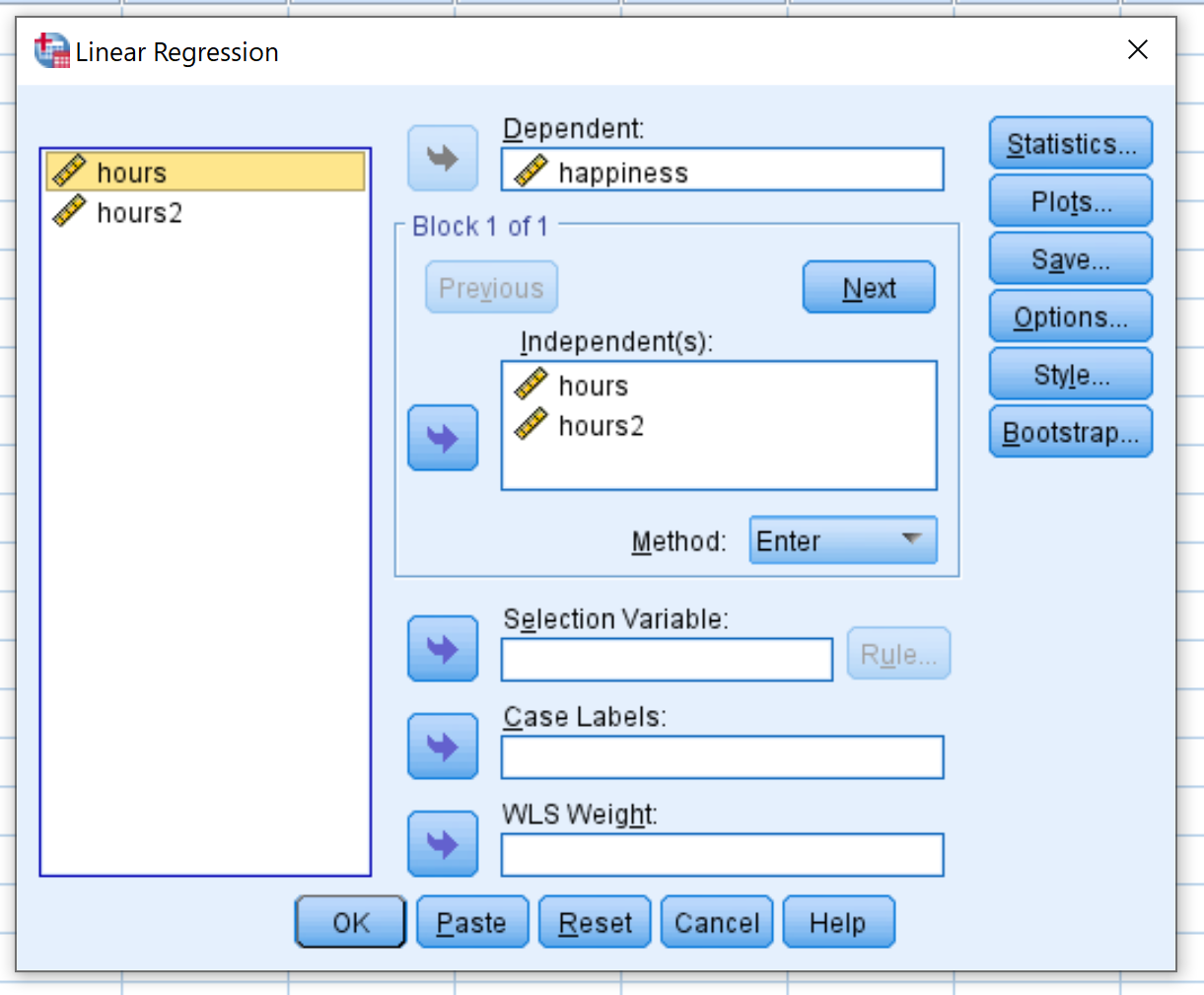
Etapa 4: interprete os resultados.

Depois de clicar em OK , os resultados da regressão quadrática aparecerão em uma nova janela.

A primeira tabela que nos interessa chama-se Resumo do Modelo :

Veja como interpretar os números mais relevantes nesta tabela:

• R Quadrado: Esta é a proporção da variância na variável resposta que pode ser explicada pelas variáveis explicativas. Neste exemplo, 90,9% da variação da felicidade pode ser explicada pelas variáveis horas e horas ² .
• Padrão. Erro de estimativa: o erro padrão é a distância média entre os valores observados e a linha de regressão. Neste exemplo, os valores observados desviam em média 9.519 unidades da linha de regressão.

A próxima tabela que nos interessa chama-se ANOVA :

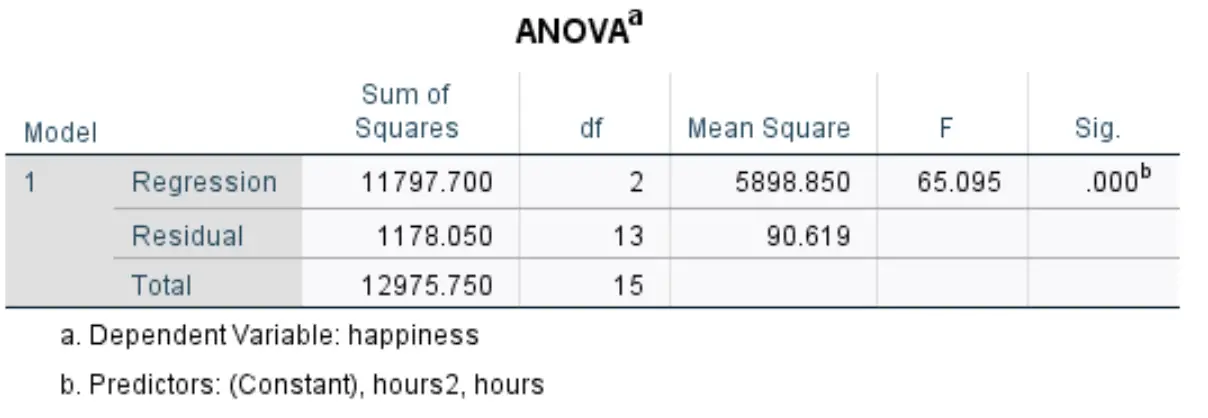
Veja como interpretar os números mais relevantes nesta tabela:

• F: Esta é a estatística F geral para o modelo de regressão, calculada como Regressão Quadrática Média / Residual Quadrático Médio.
• Sig: Este é o valor p associado à estatística F geral. Isto nos diz se o modelo de regressão como um todo é estatisticamente significativo ou não. Nesse caso, o valor p é igual a 0,000, indicando que as variáveis explicativas horas e horas ² combinadas possuem associação estatisticamente significativa com o resultado do exame.

A seguinte tabela que nos interessa intitula-se Coeficientes :

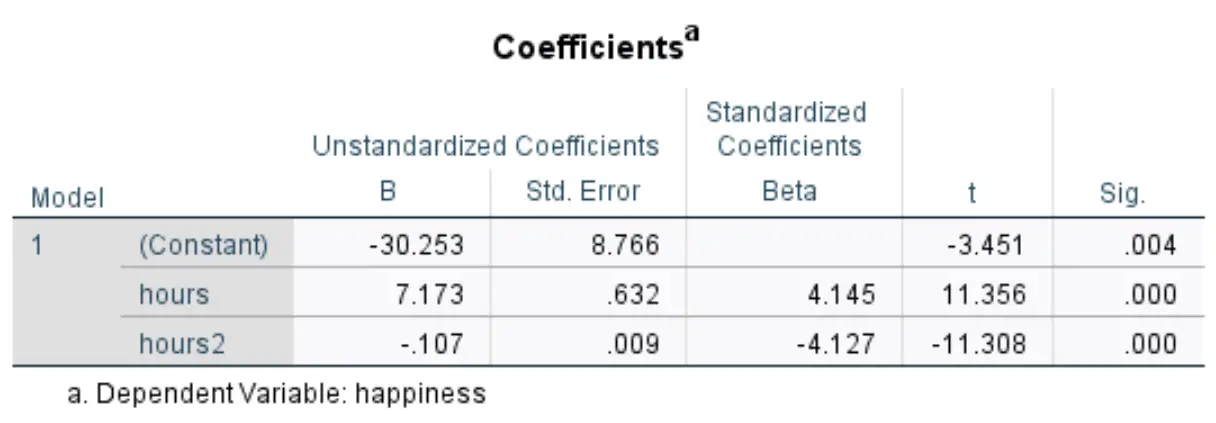
Podemos usar os valores da coluna B não padronizado para formar a equação de regressão estimada para este conjunto de dados:

Nível de felicidade estimado = -30,253 + 7,173*(horas) – 0,107*(horas ² )

Podemos usar esta equação para encontrar o nível estimado de felicidade de um indivíduo com base no número de horas trabalhadas por semana. Por exemplo, uma pessoa que trabalha 60 horas por semana deveria ter um nível de felicidade de 14,97:

Nível de felicidade estimado = -30,253 + 7,173*(60) – 0,107*(60 ² ) = 14,97 .

Por outro lado, uma pessoa que trabalha 30 horas por semana deveria ter um nível de felicidade de 88,65:

Nível de felicidade estimado = -30,253 + 7,173*(30) – 0,107*(30 ² ) = 88,65 .

Etapa 5: Relate os resultados.

Finalmente, queremos relatar os resultados da nossa regressão quadrática. Aqui está um exemplo de como fazer isso:

Foi realizada uma regressão quadrática para quantificar a relação entre o número de horas que um indivíduo trabalhou e seu correspondente nível de felicidade (medido de 0 a 100). Uma amostra de 16 pessoas foi utilizada na análise.

Os resultados mostraram que houve relação estatisticamente significativa entre as variáveis explicativas horas e horas ² e a variável resposta felicidade (F(2, 13) = 65,095, p < 0,000).

Juntas, estas duas variáveis explicativas representaram 90,9% da variabilidade da felicidade.

A equação de regressão acabou sendo:

Nível de felicidade estimado = -30,253 + 7,173 (horas) – 0,107 ( ² horas)