O que são resíduos nas estatísticas?

Um resíduo é a diferença entre um valor observado e um valor previsto na análise de regressão .

É calculado da seguinte forma:

Residual = Valor observado – Valor previsto

Lembre-se de que o objetivo da regressão linear é quantificar a relação entre uma ou mais variáveis preditoras e uma variável de resposta . Para fazer isso, a regressão linear encontra a linha que melhor “se ajusta” aos dados, chamada de linha de regressão de mínimos quadrados .

Esta linha produz uma previsão para cada observação no conjunto de dados, mas é improvável que a previsão feita pela linha de regressão corresponda exatamente ao valor observado.

A diferença entre a previsão e o valor observado é o resíduo. Se plotarmos os valores observados e sobrepormos a linha de regressão ajustada, os resíduos de cada observação seriam a distância vertical entre a observação e a linha de regressão:

Uma observação tem um resíduo positivo se o seu valor for maior que o valor previsto feito pela linha de regressão.

Por outro lado, uma observação tem um resíduo negativo se o seu valor for menor que o valor previsto feito pela linha de regressão.

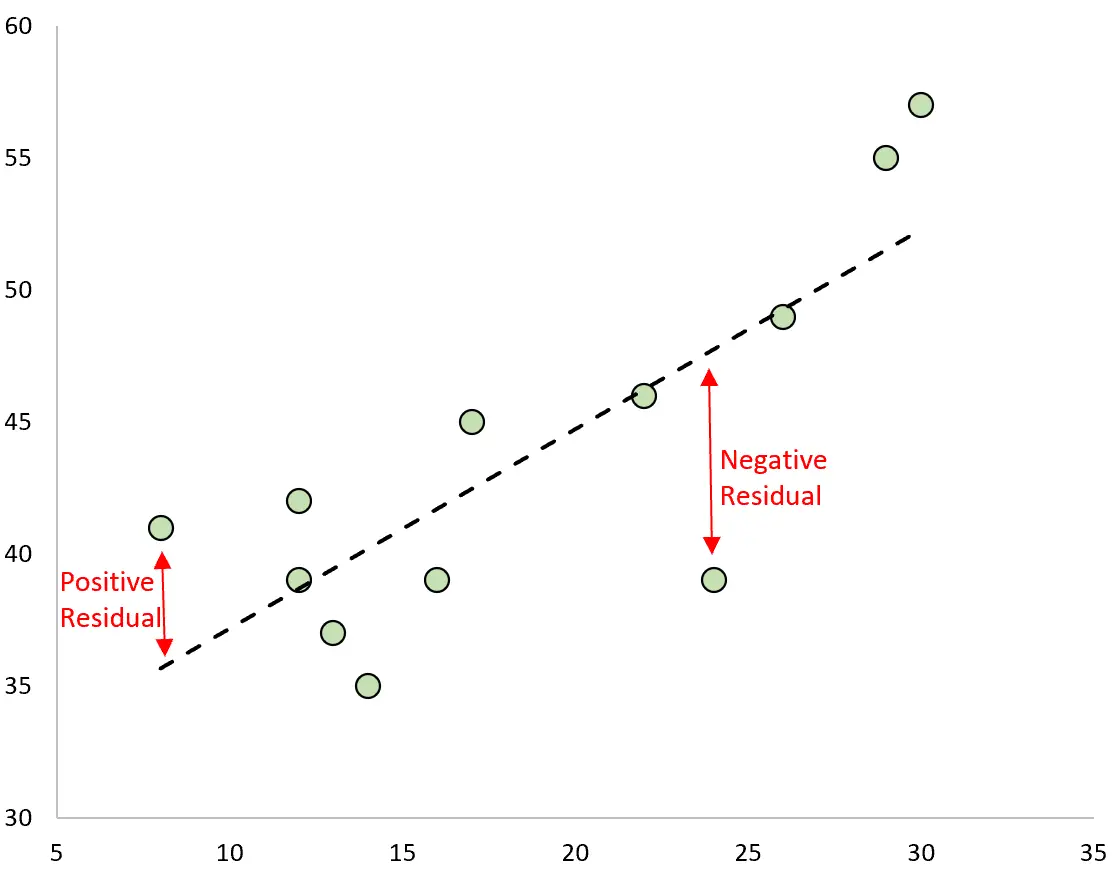
Algumas observações terão resíduos positivos, enquanto outras terão resíduos negativos, mas todos os resíduos somarão zero .

Exemplo de cálculo de resíduos

Suponha que temos o seguinte conjunto de dados com 12 observações no total:

Se usarmos software estatístico (como R , Excel , Python , Stata , etc.) para ajustar uma linha de regressão linear a este conjunto de dados, descobriremos que a linha de melhor ajuste será:

y = 29,63 + 0,7553x

Usando esta linha, podemos calcular o valor previsto para cada valor de Y com base no valor de X. Por exemplo, o valor previsto da primeira observação seria:

y = 29,63 + 0,7553*(8) = 35,67

Podemos então calcular o resíduo para esta observação da seguinte forma:

Residual = Valor observado – Valor previsto = 41 – 35,67 = 5,33

Podemos repetir este processo para encontrar o resíduo para cada observação:

Se criarmos um gráfico de dispersão para visualizar as observações com a linha de regressão ajustada, veremos que algumas das observações ficam acima da linha, enquanto outras ficam abaixo da linha:

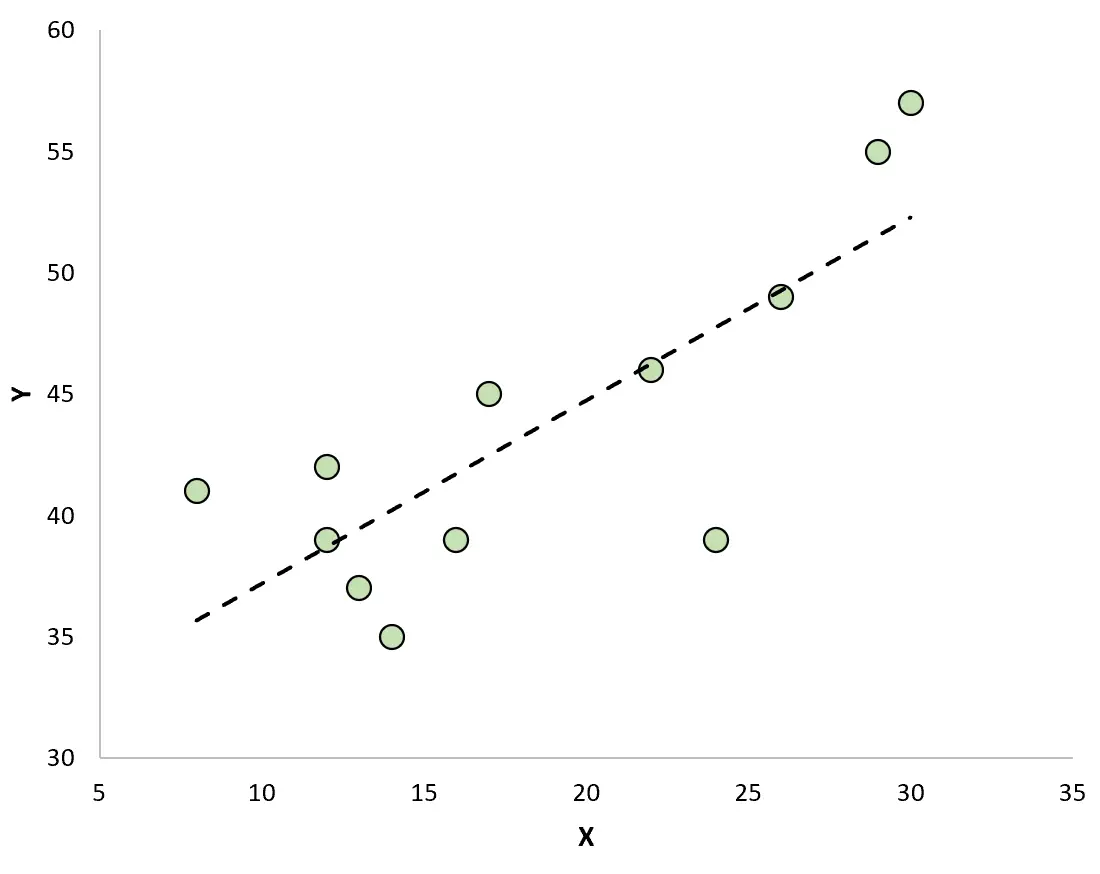
Propriedades dos resíduos

Os resíduos têm as seguintes propriedades:

• Cada observação em um conjunto de dados possui um resíduo correspondente. Portanto, se um conjunto de dados contiver 100 observações no total, o modelo produzirá 100 valores previstos, resultando em 100 resíduos no total.
• A soma de todos os resíduos é zero.
• O valor médio dos resíduos é zero.

Como os resíduos são usados na prática?

Na prática, os resíduos são usados por três razões diferentes na regressão:

1. Avalie a adequação do modelo.

Depois de produzirmos uma linha de regressão ajustada, podemos calcular a soma residual dos quadrados (RSS) , que é a soma de todos os resíduos quadrados. Quanto menor o RSS, melhor o modelo de regressão se ajusta aos dados.

2. Verifique a suposição de normalidade.

Uma das principais suposições da regressão linear é que os resíduos são normalmente distribuídos.

Para testar esta hipótese, podemos criar um gráfico QQ, que é um tipo de gráfico que podemos usar para determinar se os resíduos de um modelo seguem ou não uma distribuição normal.

Se os pontos no gráfico formarem aproximadamente uma linha reta diagonal, então a suposição de normalidade é atendida.

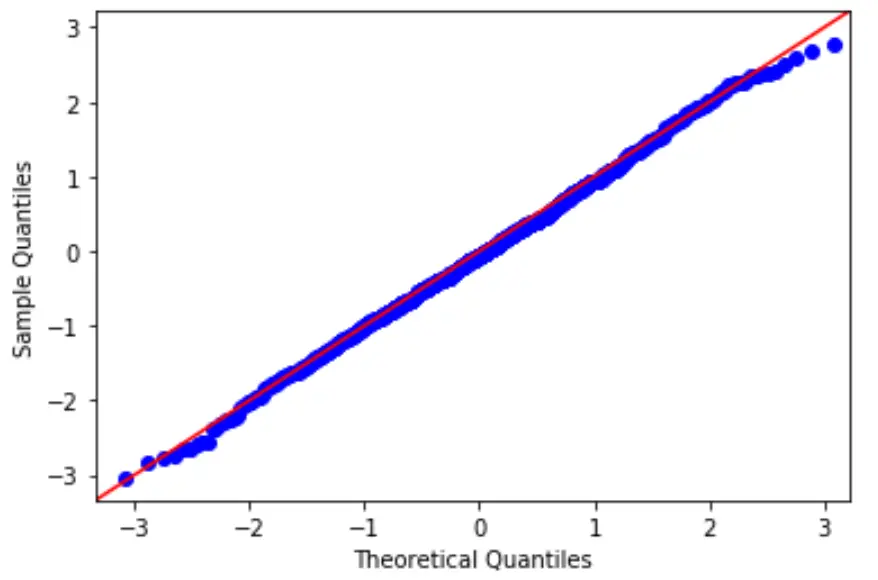
3. Verifique a suposição de homocedasticidade.

Outra suposição importante da regressão linear é que os resíduos têm variância constante em cada nível de x. Isso é chamado de homocedasticidade. Quando este não é o caso, os resíduos sofrem de heterocedasticidade .

Para verificar se essa suposição é atendida, podemos criar um gráfico de resíduos , que é um gráfico de dispersão que mostra os resíduos em relação aos valores previstos do modelo.

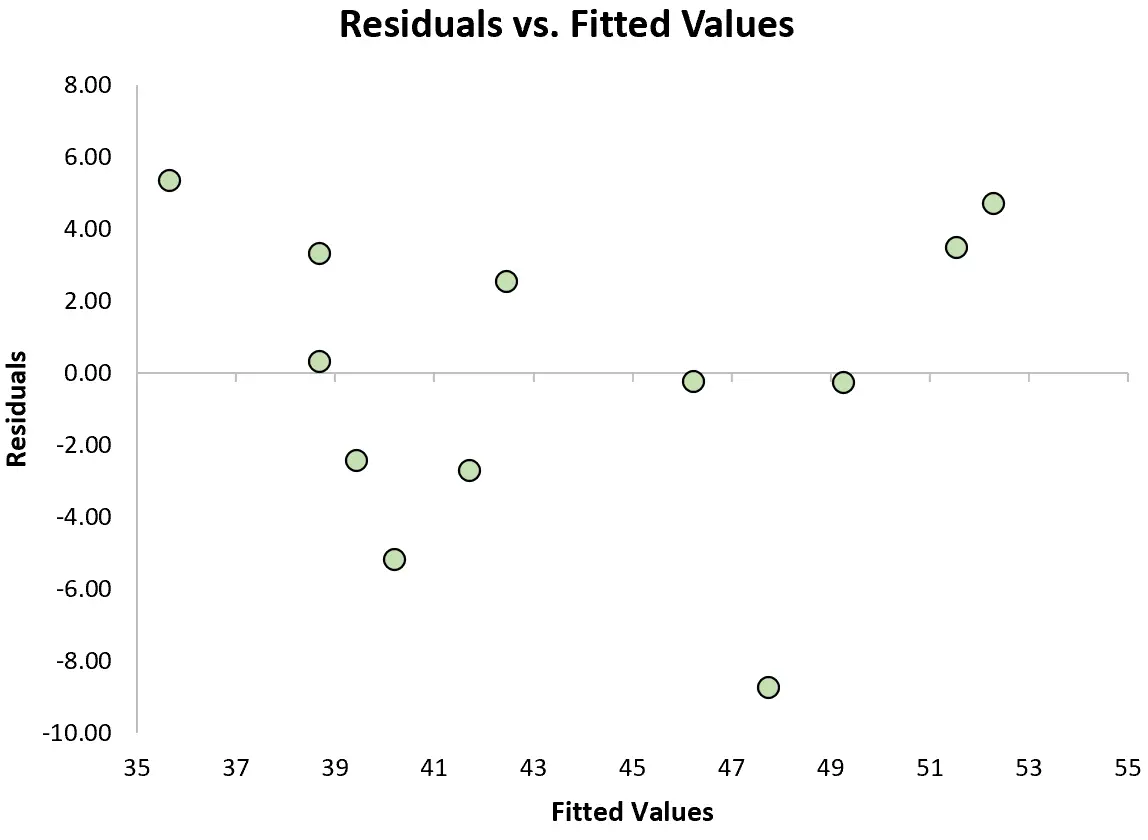
Se os resíduos estiverem distribuídos aproximadamente uniformemente em torno de zero no gráfico, sem nenhuma tendência clara, então geralmente dizemos que a suposição de homocedasticidade é atendida.

Recursos adicionais

Introdução à regressão linear simples
Introdução à regressão linear múltipla
As quatro suposições da regressão linear
Como criar um gráfico residual no Excel