O que são resíduos padronizados?

Um resíduo é a diferença entre um valor observado e um valor previsto em um modelo de regressão .

É calculado da seguinte forma:

Residual = Valor observado – Valor previsto

Se plotarmos os valores observados e sobrepormos a linha de regressão ajustada, os resíduos de cada observação seriam a distância vertical entre a observação e a linha de regressão:

Um tipo de resíduo que costumamos usar para identificar valores discrepantes em um modelo de regressão é chamado de resíduo padronizado .

É calculado da seguinte forma:

r _eu = e _eu / s(e _eu ) = e _eu / RSE√ 1-h _ii

Ouro:

• e _i : O i- ^ésimo resíduo
• RSE: erro padrão residual do modelo
• h _ii : O surgimento da ^i-ésima observação

Na prática, muitas vezes consideramos qualquer resíduo padronizado cujo valor absoluto seja superior a 3 como um valor atípico.

Isso não significa necessariamente que retiraremos essas observações do modelo, mas deveríamos pelo menos estudá-las mais a fundo para verificar se não são resultado de um erro de entrada de dados ou de algum outro evento estranho.

Nota: Às vezes, os resíduos padronizados também são chamados de “resíduos estudados internamente”.

Exemplo: Como calcular resíduos padronizados

Suponha que temos o seguinte conjunto de dados com 12 observações no total:

Se usarmos software estatístico (como R , Excel , Python , Stata , etc.) para ajustar uma linha de regressão linear a este conjunto de dados, descobriremos que a linha de melhor ajuste será:

y = 29,63 + 0,7553x

Usando esta linha, podemos calcular o valor previsto para cada valor de Y com base no valor de X. Por exemplo, o valor previsto da primeira observação seria:

y = 29,63 + 0,7553*(8) = 35,67

Podemos então calcular o resíduo para esta observação da seguinte forma:

Residual = Valor observado – Valor previsto = 41 – 35,67 = 5,33

Podemos repetir este processo para encontrar o resíduo para cada observação:

Também podemos usar software estatístico para descobrir que o erro padrão residual do modelo é 4,44 .

E, embora esteja além do escopo deste tutorial, podemos usar software para encontrar a estatística de alavancagem (h _ii ) para cada observação:

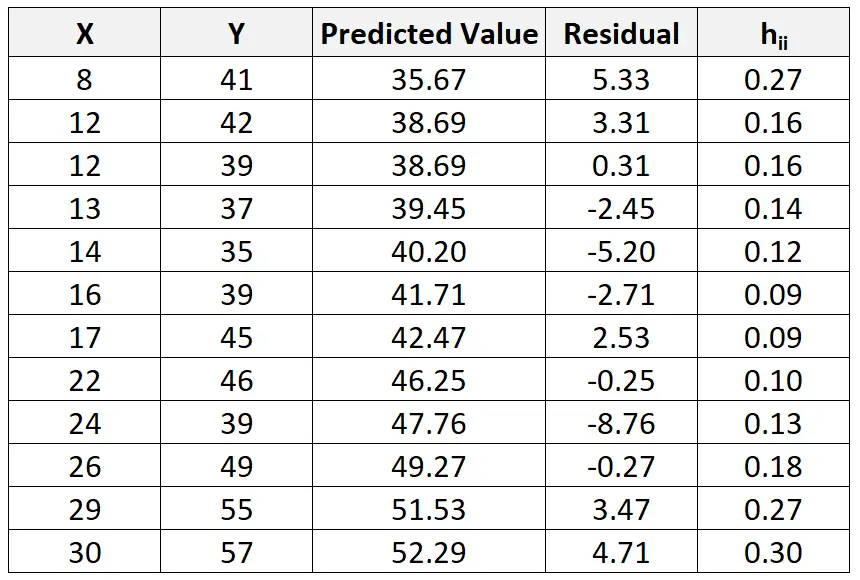
Podemos então usar a seguinte fórmula para calcular o resíduo padronizado para cada observação:

r _eu = e _eu / RSE√ 1-h _ii

Por exemplo, o resíduo padronizado para a primeira observação é calculado da seguinte forma:

_ri = 5,33 / 4,44√ 1-0,27 = 1,404

Podemos repetir este processo para encontrar o resíduo padronizado para cada observação:

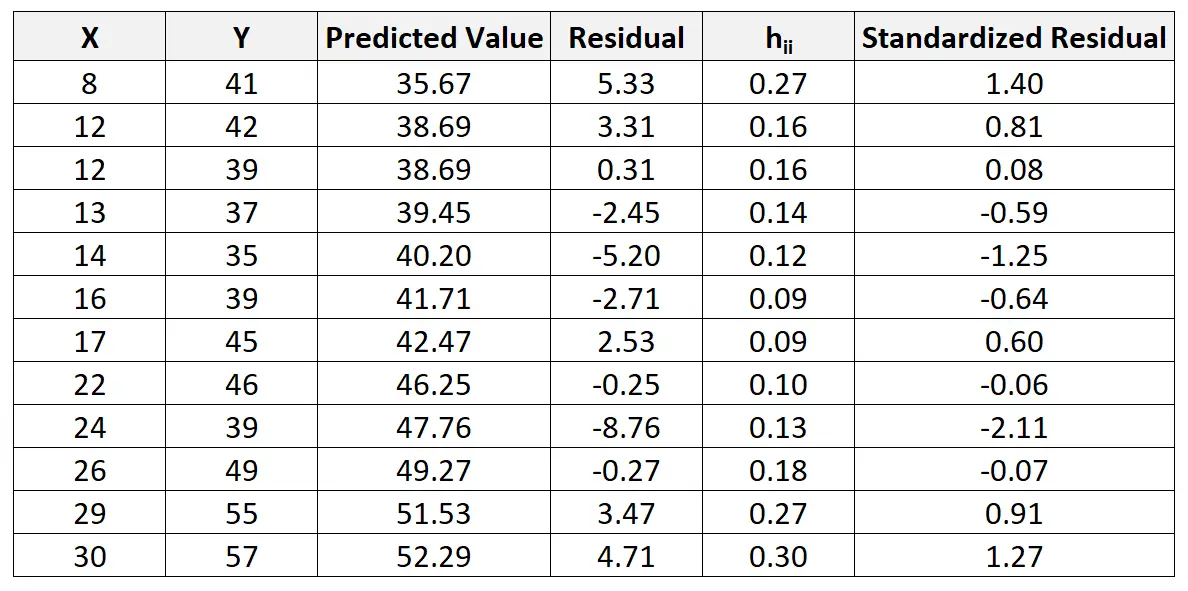
Podemos então criar um gráfico de dispersão rápido dos valores preditivos em relação aos resíduos padronizados para ver visualmente se algum dos resíduos padronizados excede um limite de valor absoluto de 3:

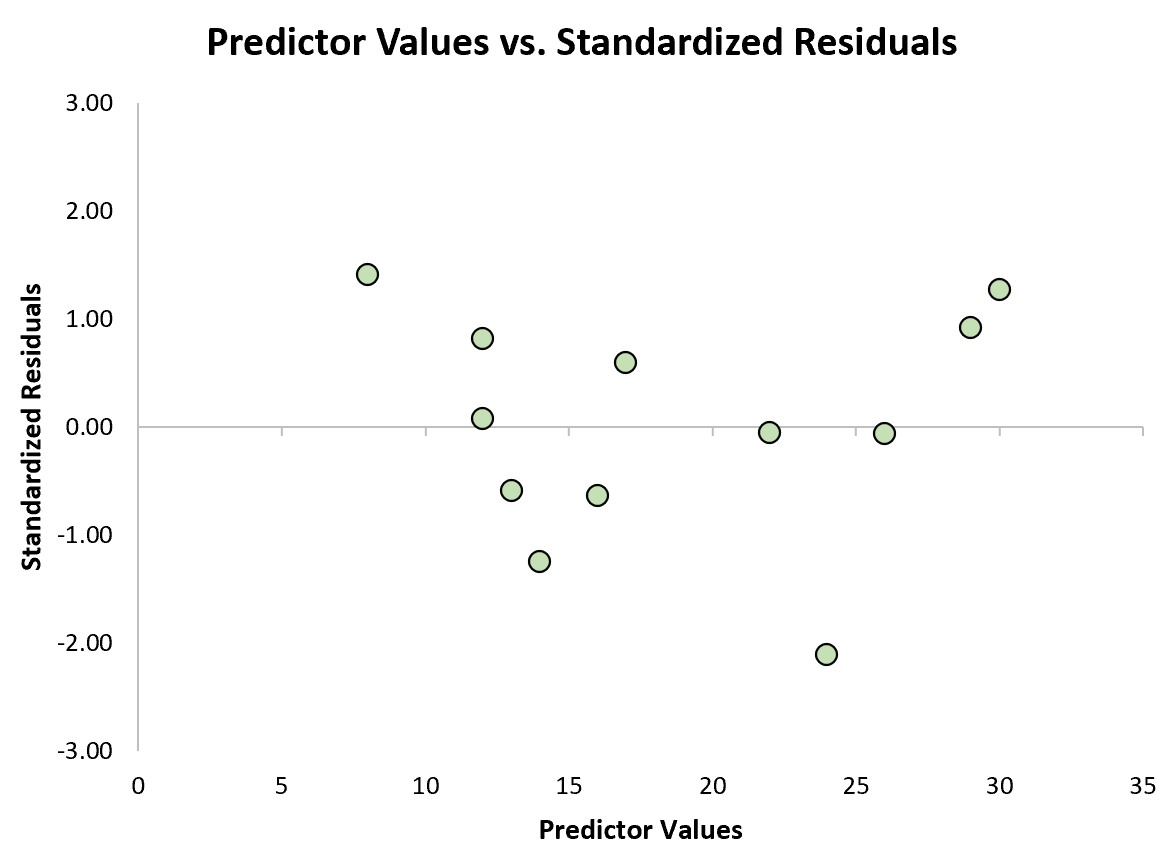
No gráfico, podemos ver que nenhum dos resíduos padronizados excede o valor absoluto de 3. Assim, nenhuma das observações parece ser atípica.

Deve-se notar que, em alguns casos, os pesquisadores consideram observações cujos resíduos padronizados excedem um valor absoluto de 2 como outliers.

Depende de você, dependendo da área em que está trabalhando e do problema específico em que está trabalhando, se deseja usar um valor absoluto de 2 ou 3 como limite para valores discrepantes.

Recursos adicionais

Os tutoriais a seguir fornecem informações adicionais sobre resíduos padronizados:

O que são resíduos nas estatísticas?
Como calcular resíduos padronizados no Excel
Como calcular resíduos padronizados em R
Como calcular resíduos padronizados em Python