Um guia suave para a soma dos quadrados: sst, ssr, sse

A regressão linear é usada para encontrar a linha que melhor “se ajusta” a um conjunto de dados.

Freqüentemente usamos três somas de quadrados diferentes para medir quão bem a linha de regressão realmente se ajusta aos dados:

1. Soma dos Quadrados Totais (SST) – A soma dos quadrados das diferenças entre os pontos de dados individuais (y _i ) e a média da variável de resposta ( y ).

• SST = Σ(y _i – y ) ²

2. Regressão da Soma dos Quadrados (SSR) – A soma dos quadrados das diferenças entre os pontos de dados previstos (ŷ _i ) e a média da variável de resposta ( y ).

• SSR = Σ(ŷ _i – y ) ²

3. Erro da Soma dos Quadrados (SSE) – A soma dos quadrados das diferenças entre os pontos de dados previstos (ŷ _i ) e os pontos de dados observados (y _i ).

• SSE = Σ(ŷ _i – y _i ) ²

Existe a seguinte relação entre estas três medidas:

SST = SSR + SSE

Portanto, se conhecermos duas destas medidas, poderemos utilizar álgebra simples para calcular a terceira.

SSR, SST e R-Quadrado

R-quadrado , às vezes chamado de coeficiente de determinação, é uma medida de quão bem um modelo de regressão linear se ajusta a um conjunto de dados. Representa a proporção da variância na variável resposta que pode ser explicada pela variável preditora.

O valor de R ao quadrado pode variar de 0 a 1. Um valor 0 indica que a variável de resposta não pode ser explicada pela variável preditora. Um valor 1 indica que a variável resposta pode ser perfeitamente explicada sem erros pela variável preditora.

Usando SSR e SST, podemos calcular o R ao quadrado da seguinte forma:

R ao quadrado = SSR / SST

Por exemplo, se o SSR para um determinado modelo de regressão for 137,5 e o SST for 156, calcularíamos o R ao quadrado da seguinte forma:

R ao quadrado = 137,5/156 = 0,8814

Isso nos diz que 88,14% da variação na variável resposta pode ser explicada pela variável preditora.

Calcule SST, SSR, SSE: exemplo passo a passo

Suponha que temos o seguinte conjunto de dados que mostra o número de horas estudadas por seis alunos diferentes, juntamente com as notas dos exames finais:

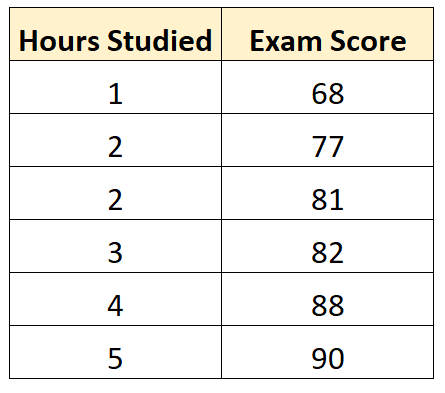
Usando algum software estatístico (como R , Excel , Python ) ou mesmo manualmente, podemos ver que a linha mais adequada é:

Pontuação = 66,615 + 5,0769*(Horas)

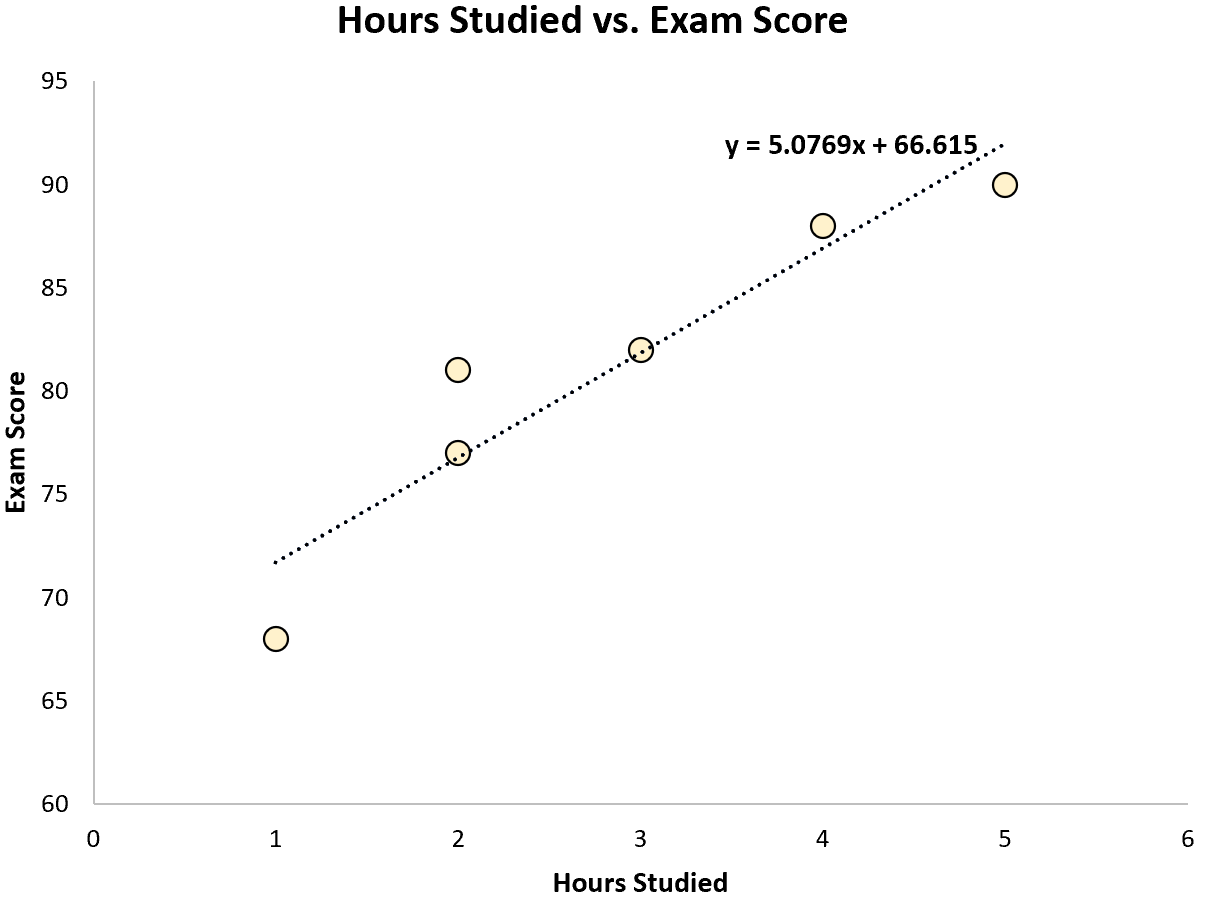
Depois de conhecermos a reta da equação de melhor ajuste, podemos usar as seguintes etapas para calcular SST, SSR e SSE:

Etapa 1: Calcule a média da variável de resposta.

A média da variável de resposta ( y ) é 81 .

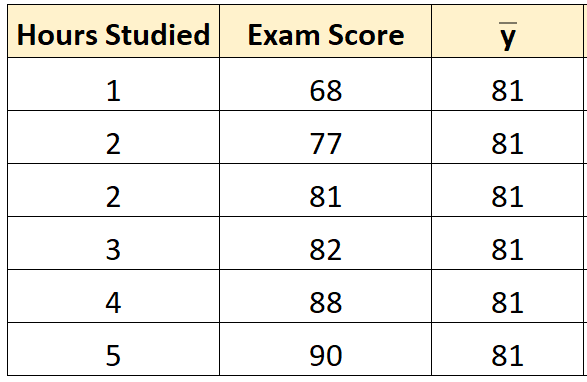
Etapa 2: Calcule o valor previsto para cada observação.

Então podemos usar a linha da equação de melhor ajuste para calcular a pontuação prevista no exame () para cada aluno.

Por exemplo, a nota prevista do exame para o aluno que estudou uma hora é:

Pontuação = 66,615 + 5,0769*(1) = 71,69 .

Podemos usar a mesma abordagem para encontrar a pontuação prevista para cada aluno:

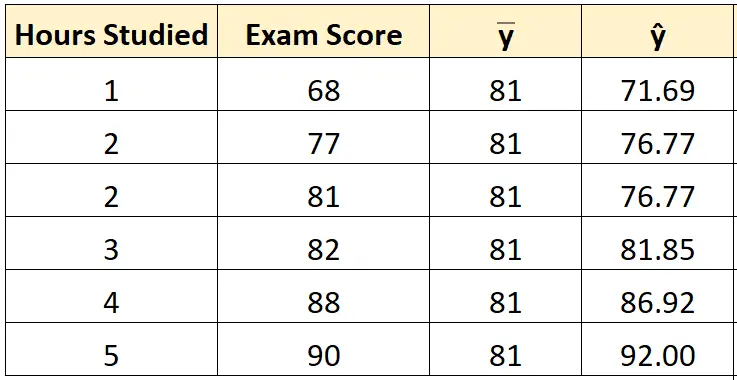
Etapa 3: Calcule a soma total dos quadrados (SST).

Então podemos calcular a soma dos quadrados no total.

Por exemplo, a soma total dos quadrados para o primeiro aluno é:

(y _eu – y ) ² = (68 – 81) ² = 169 .

Podemos usar a mesma abordagem para encontrar a soma total dos quadrados para cada aluno:

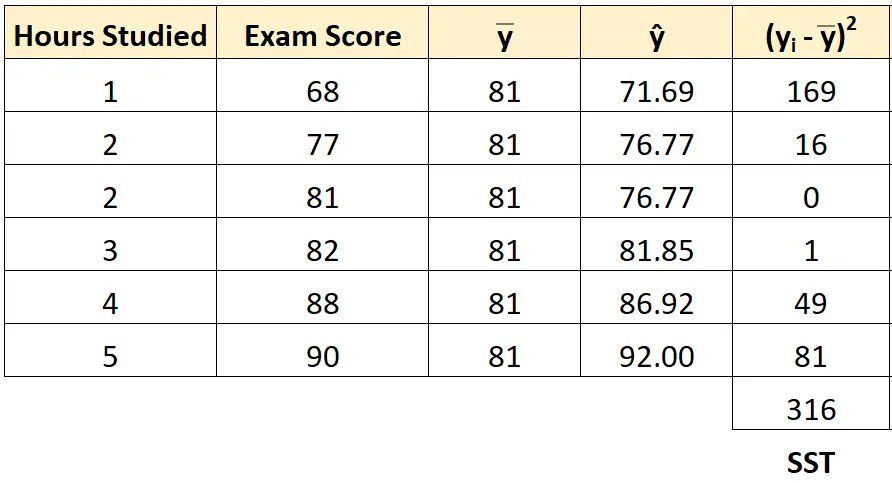
A soma total dos quadrados é 316 .

Etapa 4: Calcule a regressão da soma dos quadrados (SSR).

Então podemos calcular a regressão da soma dos quadrados.

Por exemplo, a regressão da soma dos quadrados para o primeiro aluno é:

( _ŷi – y ) ² = (71,69 – 81) ² = 86,64 .

Podemos usar a mesma abordagem para encontrar a regressão da soma dos quadrados para cada aluno:

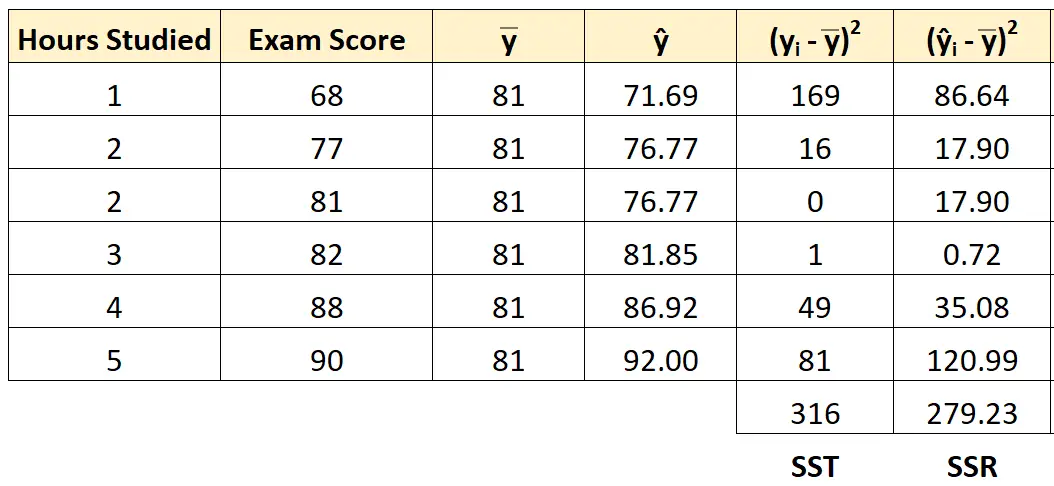
A soma da regressão dos quadrados é 279,23 .

Etapa 5: Calcule a soma dos erros quadrados (SSE).

Então podemos calcular o erro da soma dos quadrados.

Por exemplo, a soma dos erros quadrados para o primeiro aluno é:

(ŷ _i – y _i ) ² = (71,69 – 68) ² = 13,63 .

Podemos usar a mesma abordagem para encontrar a soma dos erros quadrados para cada aluno:

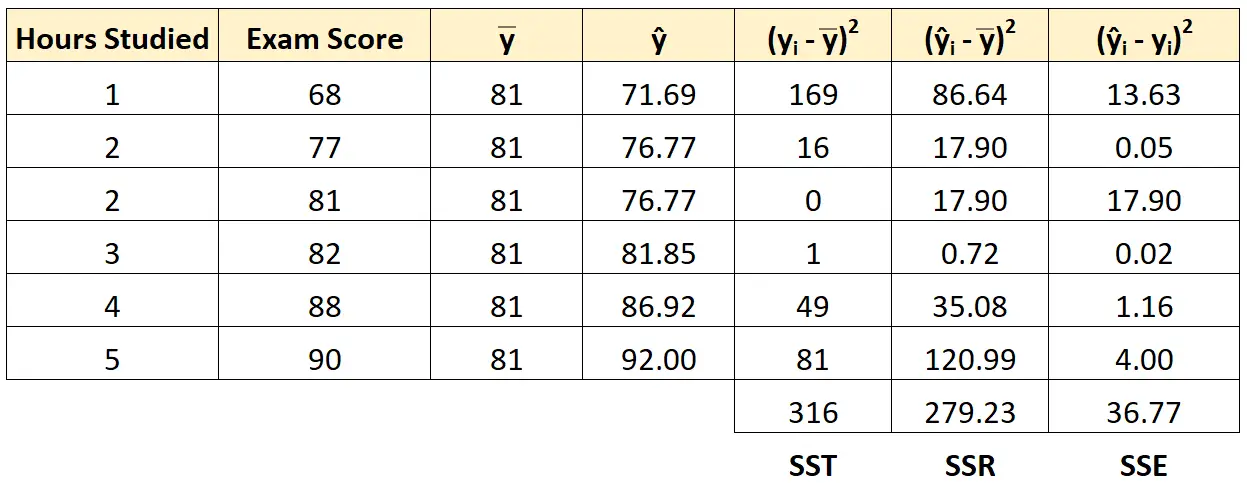
Podemos verificar que SST = SSR + SSE

• SST = SSR + SSE
• 316 = 279,23 + 36,77

Também podemos calcular o R ao quadrado do modelo de regressão usando a seguinte equação:

• R ao quadrado = SSR / SST
• R ao quadrado = 279,23/316
• R ao quadrado = 0,8836

Isso nos diz que 88,36% da variação nas notas dos exames pode ser explicada pela quantidade de horas estudadas.

Recursos adicionais

Você pode usar as seguintes calculadoras para calcular automaticamente SST, SSR e SSE para qualquer linha de regressão linear simples:

Calculadora SST
Calculadora RSS
Calculadora ESS