Tamanho da amostra

By Dr. benjamim anderson Agosto 3, 2023 Estatisticas 0 Comments

Este artigo explica o que é o tamanho da amostra e por que ele é importante nas estatísticas. Além disso, você descobrirá como calcular o tamanho de amostra apropriado e um exercício resolvido para ver como isso é feito.

Qual é o tamanho da amostra?

O tamanho da amostra (ou tamanho da amostra ) é o número de indivíduos que compõem a amostra de um estudo. Nas estatísticas, o tamanho da amostra é importante para que a amostra seja representativa de toda a população.

Portanto, o tamanho da amostra de um estudo estatístico deve ser grande o suficiente para representar as características de toda a população. Por outro lado, o tamanho da amostra não pode ser excessivamente grande, pois a pesquisa fica mais cara. Concluindo, o tamanho da amostra deve ser adequado, nem muito grande nem muito pequeno.

Por exemplo, se quisermos fazer uma análise sobre a altura de um país, não podemos pedir a altura de todos os habitantes do país, porque o levantamento demoraria muito e seria muito caro. É, portanto, necessário realizar uma amostragem aleatória e entrevistar apenas uma amostra representativa da população.

➤ Veja: Tipos de amostragem

E como podemos saber o tamanho apropriado da amostra? Na próxima seção, veremos como determinar o tamanho de amostra apropriado com base nos requisitos da pesquisa.

Como calcular o tamanho da amostra

Para estimar uma média, o tamanho da amostra necessário é igual ao quadrado de Z _α/2 multiplicado pelo desvio padrão (σ) dividido pela margem de erro desejada (e). A fórmula para calcular o tamanho da amostra é, portanto:

$\displaystyle n=\left(\frac{Z_{\alpha/2}\cdot\sigma}{e}\right)^2$

Ouro:

$n$

é o tamanho da amostra.
$\alpha$

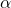
é o nível de significância desejado. Levando em conta isso

$1-\alpha$

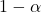
é o nível de confiança desejado.
$Z_{\alpha/2}$

é o quantil da distribuição normal padrão correspondente a uma probabilidade de α/2. Para amostras grandes e nível de confiança de 95% é geralmente próximo de 1,96 e para nível de confiança de 99% é geralmente próximo de 2,576.
$\sigma$

é o desvio padrão.

Tenha em mente que nesta fórmula se assume que o tamanho da população é infinito, ou seja, o tamanho da população é muito grande ou desconhecido.

Nota: A fórmula acima é derivada do intervalo da fórmula de confiança para a média .

Exemplo de cálculo do tamanho da amostra

Nesta seção, calcularemos o tamanho de amostra apropriado para uma pesquisa estatística como exemplo.

Sabemos que o desvio padrão de uma população ronda os 15, mas não sabemos a sua média, por isso queremos fazer um estudo para estimar a média. Qual tamanho de amostra precisamos se quisermos uma margem de erro de ±2 com um nível de confiança de 95%?

Como vimos acima, a fórmula para calcular o tamanho da amostra é:

$\displaystyle n=\left(\frac{Z_{\alpha/2}\cdot\sigma}{e}\right)^2$

Neste caso, o nível de confiança desejado é de 95%, portanto o valor Z _α/2 correspondente é 1,96.

$1-\alpha=0,95 \ \color{orange}\bm{\longrightarrow}\color{black} \ \alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}Z_{\alpha/2}= \ \color{orange}\bm{?}\\[4ex]Z_{0,025}=1,96\end{array}$

➤ Veja: Tabela com valores de nível de confiança

Por fim, agora que sabemos quanto valem todos os parâmetros, substituímos seus valores na fórmula e calculamos o tamanho da amostra:

$\begin{aligned}\displaystyle n&=\left(\frac{Z_{\alpha/2}\cdot\sigma}{e}\right)^2\\[2ex] n&=\left(\frac{1,96\cdot 15}{2}\right)^2\\[2ex] n&=216,09 \approx 217 \end{array}$

Resumindo, para estimar a média populacional com os requisitos desejados, precisamos de pelo menos uma amostra de 217 indivíduos.

Tamanho da amostra, nível de confiança e margem de erro

Dependendo do nível de confiança e da margem de erro exigida, o tamanho da amostra necessária irá variar. Assim, o tamanho da amostra, o nível de confiança e a margem de erro estão relacionados da seguinte forma:

O tamanho da amostra e o nível de confiança são diretamente proporcionais. Ou seja, se o nível de confiança aumentar, o tamanho da amostra também aumentará.
O tamanho da amostra e a margem de erro são inversamente proporcionais. Portanto, se a margem de erro aumentar, o tamanho da amostra diminuirá.
Portanto, aumentar o tamanho da amostra pode aumentar o nível de confiança ou reduzir a margem de erro.

Outras fórmulas de tamanho de amostra

Dependendo do parâmetro a ser estimado, a fórmula para o tamanho da amostra necessária varia ligeiramente. Portanto, nesta seção veremos outras fórmulas que podem ser úteis para calcular o tamanho da amostra em alguns casos especiais.

tamanho da amostra de uma proporção

A fórmula para calcular o tamanho da amostra necessária para estimar uma proporção (p) é:

$n=\cfrac{N\cdot Z_{\alpha/2}^2\cdot p\cdot (1-p)}{e^2\cdot (N-1)+Z_{\alpha/2}^2\cdot p\cdot (1-p)}$

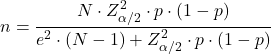
Tamanho da amostra de uma probabilidade

Quando você deseja estimar uma probabilidade, é recomendado usar a seguinte fórmula para determinar o tamanho de amostra necessário:

$\displaystyle n=\left(\frac{Z_{\alpha/2}}{2\cdot e}\right)^2$

Tamanho da amostra para comparação de duas médias independentes

A fórmula para calcular o tamanho da amostra ao comparar duas médias independentes com um determinado risco α e risco β é a seguinte:

$n=\cfrac{2\cdot \sigma^2 \cdot \left(Z_{\alpha/2}+Z_\beta\right)}{\Delta^2}$

Ouro

$\Delta$

é a diferença entre as duas médias da hipótese alternativa.

Tamanho da amostra para comparação de duas médias pareadas

Se você quiser comparar duas médias emparelhadas com erro fixo α e erro β, a fórmula a ser usada para encontrar o número de observações na amostra é:

$n=\cfrac{2\cdot \sigma_d^2 \cdot \left(Z_{\alpha/2}+Z_\beta\right)}{\Delta^2}$

Ouro

$\Delta$

é a diferença entre as duas médias pareadas da hipótese alternativa e

$\sigma_d^2$

É a variância das diferenças entre duas medidas do mesmo indivíduo.

About Author

Dr. benjamim anderson

Olá, sou Benjamin, um professor aposentado de estatística que se tornou professor dedicado na Statorials. Com vasta experiência e conhecimento na área de estatística, estou empenhado em compartilhar meu conhecimento para capacitar os alunos por meio de Statorials. Saber mais