Teorema de bayes

By Agosto 1, 2023 Probabilidade 0 Comments

Este artigo explica o que é o teorema de Bayes e para que ele é usado em probabilidade e estatística. Assim, você descobrirá qual é a fórmula do teorema de Bayes, exemplos resolvidos do teorema de Bayes e quais as aplicações deste teorema.

Qual é o teorema de Bayes?

Na teoria da probabilidade, o teorema de Bayes é uma lei usada para calcular a probabilidade de um evento quando informações a priori sobre esse evento são conhecidas.

Mais especificamente, o teorema de Bayes relaciona matematicamente a probabilidade do evento A dado o evento B com a probabilidade de B dado A.

Por exemplo, se você souber antecipadamente a probabilidade de uma pessoa ter dor de cabeça quando estiver gripada, poderá usar o teorema de Bayes para determinar a probabilidade de uma pessoa ter gripe quando tiver dor de cabeça.

O teorema de Bayes tem muitas aplicações, por exemplo, é usado em medicina, economia ou tecnologia para calcular as probabilidades de certos eventos condicionados por outros eventos. A seguir entraremos em detalhes sobre as diferentes aplicações do teorema de Bayes.

O teorema de Bayes foi inventado pelo matemático inglês Thomas Bayes (1702-1761), embora tenha sido publicado postumamente em 1763.

Fórmula do teorema de Bayes

O teorema de Bayes diz que dado um espaço amostral composto por um conjunto de eventos mutuamente exclusivos {A 1 , A 2 ,…, A i ,…, A n } cujas probabilidades não são zero e outro evento B , podemos relacionar matematicamente a condicional probabilidade de A i dado o evento B com a probabilidade condicional de B dado A i .

Portanto, a fórmula do teorema de Bayes , também conhecido como regra de Bayes , é:

Fórmula do teorema de Bayes, regra de Bayes

Ouro:

  • P(A_i|B)

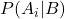
    é a probabilidade condicional do evento A i dado o evento B, chamada de probabilidade posterior.

  • P(B|A_i)

    é a probabilidade condicional do evento B dado o evento A i .

  • P(A_i)

    é a probabilidade de que o evento A i ocorra, chamada de probabilidade a priori.

Observe que o denominador da fórmula do teorema de Bayes é a probabilidade total do evento B.

Exemplo do teorema de Bayes

Assim que vermos a definição do Teorema de Bayes e qual é sua fórmula, veremos um exemplo resolvido de como uma probabilidade é calculada com o Teorema de Bayes para melhor entender o conceito.

  • Uma loja de eletrônicos vende três marcas de televisores: X, Y, Z. Estima-se que 20% das vendas são de televisores da marca com defeito, 3% dos televisores da marca Y estão com defeito e 4% dos televisores da marca Z estão com defeito. Dada uma TV com defeito, qual é a probabilidade de ser uma TV da Marca Z?

O exercício nos dá as probabilidades de um cliente comprar cada marca de televisão:

  • Evento A 1 : Um cliente compra uma televisão da marca X → P(A 1 )=0,20
  • Evento A 2 : Um cliente compra uma televisão da marca Y → P(A 2 )=0,50
  • Evento A 3 : Um cliente compra uma televisão da marca Z → P(A 3 )=0,30

Além disso, a leitura também nos dá a probabilidade de uma televisão de cada marca estar com defeito:

Evento B: A TV está com defeito

  • B|A 1 : Dado um televisor da marca X, o televisor está com defeito → P(B|A 1 )=0,05
  • B|A 2 : Dada uma televisão da marca Y, a televisão está com defeito → P(B|A 2 )=0,03
  • B|A 3 : Dado um televisor da marca Z, o televisor está com defeito → P(B|A 3 )=0,04

Portanto, a árvore de probabilidade de todos os eventos que nos interessam é a seguinte:

Diagrama de árvore do teorema de Bayes

Assim, para calcular a probabilidade de, dada uma televisão com defeito, ela ser da marca Z, devemos utilizar a fórmula do teorema de Bayes:

P(A_i|B)=\cfrac{P(B|A_i)\cdot P(A_i)}{\displaystyle \sum_{k=1}^n P(B|A_k)\cdot P(A_k)}

Usando a terminologia usada neste exemplo, a fórmula de Bayes fica assim:

P(A_3|B)=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}

Assim, o cálculo da probabilidade de um determinado televisor com defeito ser da marca Z é o seguinte:

\begin{aligned}P(A_3|B)&=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}\\[2ex]&=\cfrac{0,04\cdot 0,30}{0,05\cdot 0,20+0,03\cdot 0,50+0,04\cdot 0,30}\\[2ex]&=0,32\end{aligned}

Concluindo, a probabilidade de que, se uma televisão estiver com defeito, seja da marca Z é de 32%.

Aplicações do teorema de Bayes

Existem muitas aplicações do teorema de Bayes, incluindo:

  1. Testes médicos : o teorema de Bayes é frequentemente usado na medicina para determinar a probabilidade de aprovação em testes de diagnóstico. Por exemplo, no caso de um teste de VIH, o teorema pode ser utilizado para calcular a probabilidade de uma pessoa realmente ter o vírus se o resultado do teste for positivo.
  2. Análise Financeira : Em finanças, o teorema de Bayes é usado para calcular a probabilidade de que certos eventos econômicos, como um aumento ou diminuição no valor das ações, ocorram dado um conjunto de variáveis econômicas.
  3. Pesquisa de mercado : o teorema de Bayes permite determinar, por exemplo, a probabilidade de uma pessoa comprar um produto após ver uma propaganda desse produto.
  4. Previsão do tempo : Os modelos meteorológicos também usam o teorema de Bayes para determinar a probabilidade de que uma determinada previsão do tempo com base nos dados observados se torne realidade. Isto melhora a precisão das previsões climáticas.
  5. Segurança Informática – Na segurança cibernética, o teorema de Bayes pode ser aplicado para determinar a probabilidade de uma atividade suspeita ser realmente um ataque ao sistema informático.

Problemas resolvidos do Teorema de Bayes

Exercício 1

Estima-se que 1% da população sofra de alguma doença. Um teste para detectar esta doença tem 95% de precisão para casos positivos e 90% de precisão para casos negativos. Se o teste de uma pessoa selecionada aleatoriamente for positivo, qual é a probabilidade de ela realmente ter a doença?

A declaração de exercício nos dá as seguintes probabilidades:

A 1 : A pessoa tem a doença → P(A 1 )=0,01
A 2 : A pessoa não tem a doença → P(A 2 )=0,99

B: O teste é positivo
B|A 1 : O teste é positivo quando a pessoa tem a doença → P(B|A 1 )=0,95
B|A 2 : O teste é positivo quando a pessoa não tem a doença → P(B|A 2 )=1-0,90=0,10

Então, para calcular a probabilidade de uma pessoa selecionada aleatoriamente realmente ter a doença quando o teste for positivo, a regra de Bayes deve ser aplicada:

P(A_i|B)=\cfrac{P(B|A_i)\cdot P(A_i)}{\displaystyle \sum_{k=1}^n P(B|A_k)\cdot P(A_k)}

P(A_1|B)=\cfrac{P(B|A_1)\cdot P(A_1)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)}

Então substituímos os valores na fórmula e realizamos o cálculo de probabilidade:

\begin{aligned}P(A_1|B)&=\cfrac{P(B|A_1)\cdot P(A_1)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)}\\[2ex]&=\cfrac{0,95\cdot 0,01}{0,95\cdot 0,01+0,10\cdot 0,99}\\[2ex]&=0,0876\end{aligned}

Resumindo, a probabilidade de uma pessoa escolhida aleatoriamente testar positivo e realmente ter a doença é de 8,76%.

Exercício 2

Estima-se que a probabilidade de uma ação subir em um dia é de 40%, de permanecer estável é de 10% e de cair é de 50%. Além disso, sabemos que quando o mercado sobe, há 90% de probabilidade de um analista financeiro o prever correctamente, que quando o mercado permanece estável, a probabilidade de a previsão estar correcta é de 75% e que em caso de declínio, a probabilidade de uma previsão correta é de 75%. 85%.%. Se um analista prevê que o mercado cairá, qual a probabilidade de que ele realmente caia?

Neste caso, a declaração de exercício nos fornece as seguintes probabilidades:

A 1 : O mercado sobe em um dia → P(A 1 )=0,40
A 2 : O mercado permanece estável durante um dia → P(A 2 )=0,10
A 3 : O mercado sobe em um dia → P(A 3 )=0,50

B: O analista prevê que o mercado cairá
B|A 1 : O analista prevê corretamente que o mercado aumentará → P(B|A 1 )=0,90
B|A 2 : O analista prevê corretamente que o mercado permanece estável → P(B|A 2 )=0,75
B|A 3 : O analista prevê corretamente que o mercado vai cair → P(B|A 3 )=0,85

Para determinar a probabilidade de um analista fazer uma previsão de que o mercado cairá e que está correta, precisamos usar a fórmula do Teorema de Bayes:

P(A_i|B)=\cfrac{P(B|A_i)\cdot P(A_i)}{\displaystyle \sum_{k=1}^n P(B|A_k)\cdot P(A_k)}

P(A_3|B)=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}

Substituímos os valores de probabilidade na fórmula de Bayes e calculamos a probabilidade:

\begin{aligned}P(A_3|B)&=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}\\[2ex]&=\cfrac{0,85\cdot 0,50}{0,90\cdot 0,40+0,75\cdot 0,10+0,85\cdot 0,50}\\[2ex]&=0,4942\end{aligned}

Portanto, a probabilidade de um analista estar certo ao dizer que a bolsa vai cair é de 49,42%.

About Author

Dr. Benjamin Anderson
Dr. benjamim anderson

Olá, sou Benjamin, um professor aposentado de estatística que se tornou professor dedicado na Statorials. Com vasta experiência e conhecimento na área de estatística, estou empenhado em compartilhar meu conhecimento para capacitar os alunos por meio de Statorials. Saber mais

Add a Comment

O seu endereço de email não será publicado. Campos obrigatórios marcados com *