Teorema de chebyshev

Este artigo explica o que é o teorema de Chebyshev. Aqui você encontrará a fórmula do teorema de Chebyshev, um exercício resolvido e, além disso, uma calculadora online do teorema de Chebyshev. Por fim, mostra a diferença entre o teorema de Chebyshev e a regra empírica.

Qual é o teorema de Chebyshev?

O teorema de Chebyshev , também conhecido como desigualdade de Chebyshev , é uma regra estatística usada para calcular a probabilidade de um valor de uma variável aleatória estar a uma certa distância de sua média.

Em outras palavras, em estatística, o teorema de Chebyshev é usado para determinar a probabilidade de um valor estar dentro de um intervalo de confiança.

Além disso, o teorema de Chebyshev também é usado para provar outros teoremas estatísticos, como a lei dos grandes números.

Embora o teorema de Chebyshev tenha sido formulado pela primeira vez pelo francês Irénée-Jules Bienaymé, o teorema tem esse nome porque foi originado pelo russo Pafnuty Chebushev em 1867.

Fórmula do teorema de Chebyshev

O teorema de Chebyshev diz que a probabilidade de um valor ser igual a k desvios padrão da média é maior ou igual a um menos a razão de um dividido por k ao quadrado.

Portanto, a fórmula do teorema de Chebyshev é a seguinte:

Ouro

é o valor da variável aleatória,

a média aritmética da variável,

seu desvio padrão e

o número de desvios padrão da média sobre os quais a probabilidade deve ser calculada.

Observe que esta fórmula só pode ser utilizada se o número de desvios padrão sobre os quais o cálculo é realizado for maior que 1, ou seja, se k for maior que 1.

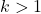Você pode usar a calculadora online do Teorema de Chebyshev abaixo para calcular a probabilidade.

Exemplo do teorema de Chebyshev

Depois de vermos a definição do teorema de Chebyshev e qual é sua fórmula, aqui está um exemplo resolvido deste teorema estatístico para melhor compreender o conceito.

• Se as notas obtidas nas estatísticas dos cursos de uma universidade são definidas por uma distribuição com média 65 e desvio padrão de 10, que porcentagem de alunos obteve nota entre 50 e 80?

Para resolver este problema, precisamos aplicar a fórmula do teorema de Chebyshev. Porém, devemos primeiro determinar quantos desvios padrão os valores 50 e 80 estão da média da variável, para isso basta fazer o seguinte cálculo:

Portanto, os valores 50 e 80 correspondem a 1,5 desvios padrão da média inferior e superior, respectivamente. Portanto, usamos a fórmula do teorema de Chebysheva com k=1,5:

Assim, pelo menos 55,56% dos alunos obtiveram nota entre 50 e 80.

Calculadora do Teorema de Chebyshev

Insira o número de desvios padrão entre os valores em questão e a média (k) e clique em “Calcular”. A calculadora retornará então a probabilidade mínima do intervalo de confiança.

Você deve inserir o número de desvios padrão usando o ponto como separador decimal.

Teorema de Chebyshev e regra prática

Dois conceitos intimamente relacionados em estatística são o teorema de Chebyshev e a regra empírica, uma vez que ambos são usados para calcular a probabilidade de intervalos de confiança.

A diferença entre o teorema de Chebyshev e a regra empírica é que o teorema de Chebyshev pode ser usado em qualquer tipo de distribuição, enquanto a regra empírica só é válida para uma distribuição normal.

A utilização do teorema de Chebyshev é, portanto, mais ampla, mas a regra empírica fornece resultados mais precisos para uma distribuição normal.

Clique aqui para ver exatamente qual é a regra prática: