Teorema do limite central

Este artigo explica o que é o teorema do limite central (CLT) e para que ele é usado nas estatísticas. Você também encontrará qual é a fórmula do teorema do limite central e um exemplo de sua aplicação resolvida passo a passo.

Qual é o teorema do limite central?

Nas estatísticas, o teorema do limite central , também chamado de teorema do limite central , afirma que a distribuição das médias amostrais se aproxima de uma distribuição normal à medida que o tamanho da amostra aumenta, independentemente da distribuição de probabilidade da população.

Ou seja, o teorema do limite central diz que se tomarmos um número suficientemente grande de amostras, a média dessas amostras pode ser aproximada a uma distribuição normal.

Além disso, o teorema do limite central afirma que a média da amostra se aproximará do valor da média da população à medida que o tamanho da amostra aumenta. Isso nos permite aproximar os parâmetros da população estatística. Abaixo veremos como isso é feito.

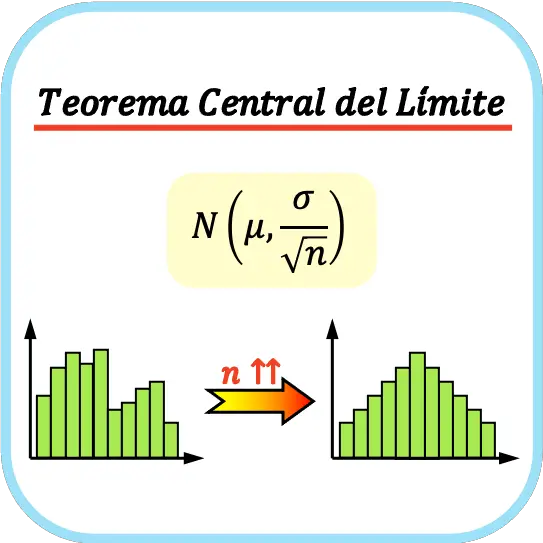
Em geral, considera-se que para aplicar o teorema do limite central o tamanho da amostra deve ser de no mínimo 30 observações, embora isso dependa das características da variável estudada.

O teorema do limite central tem muitas aplicações, uma vez que a distribuição normal permite cálculos estatísticos inferenciais, como testes de hipóteses ou intervalos de confiança. Por exemplo, em finanças, o teorema do limite central é usado para analisar o retorno e o risco de um investimento.

Exemplo do teorema do limite central

Depois de vermos a definição do teorema do limite central, vejamos um exemplo para compreender completamente o seu significado.

Um exemplo do teorema do limite central é o lançamento de um dado. O lançamento do dado segue uma distribuição discreta e uniforme , uma vez que todos os resultados são equiprováveis. Mas a distribuição da soma de vários resultados aproxima-se de uma distribuição normal.

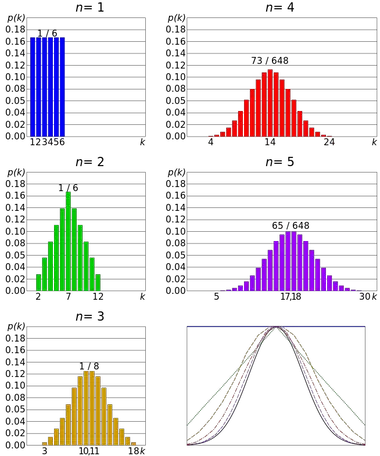
Assim, quanto mais lançamentos houver, mais provável será que a forma da distribuição das médias tenda a assemelhar-se ao gráfico da distribuição normal.

Fórmula do Teorema do Limite Central

O teorema do limite central afirma que se uma população tem média μ e desvio padrão σ e tomamos um número suficientemente grande de amostras (n≥30), o conjunto de médias amostrais pode ser aproximado a uma distribuição normal com média μ e desvio padrão σ /√n.

Além disso , _se X _{1 ,} para uma distribuição normal definida pela seguinte fórmula:

Exercício resolvido do teorema do limite central

Para que você possa assimilar totalmente o conceito, aqui está um exercício resolvido do teorema do limite central.

• Uma empresa vende peças que são usadas para substituir determinados componentes de brinquedos. Uma moeda tem peso médio de 300 g e desvio padrão de 50 g. Se um cliente encomendou um lote de 100 peças, qual é a probabilidade de que o peso médio das peças do lote seja superior a 305 g? E qual é a probabilidade de um lote de 100 peças pesar mais de 31 kg?

Como o tamanho do lote é grande (n=100), podemos aplicar o teorema do limite central para resolver o problema.

Assim, usando a fórmula do teorema do limite central, a distribuição das médias amostrais pode ser aproximada a uma distribuição normal com os seguintes parâmetros:

Agora realizamos o processo de digitação para que possamos então encontrar a probabilidade que o exercício nos pede. Para fazer isso, precisamos subtrair a média da distribuição e depois dividir pelo desvio padrão:

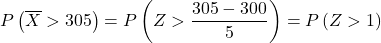tabela de distribuição normal :

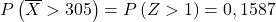
Então refazemos o processo de digitação, depois encontramos a segunda probabilidade que o problema nos pede:

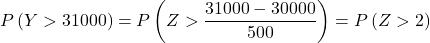
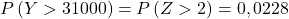➤ Veja: Lei dos grandes números