Como aplicar o teorema do limite central em r (com exemplos)

O teorema do limite central afirma que a distribuição amostral de uma média amostral é aproximadamente normal se o tamanho da amostra for grande o suficiente, mesmo que a distribuição populacional não seja normal.

O teorema do limite central também afirma que a distribuição amostral terá as seguintes propriedades:

1. A média da distribuição amostral será igual à média da distribuição populacional:

x = µ

2. O desvio padrão da distribuição amostral será igual ao desvio padrão da distribuição populacional dividido pelo tamanho da amostra:

s = σ /n

O exemplo a seguir mostra como aplicar o teorema do limite central em R.

Exemplo: aplicação do teorema do limite central em R

Suponha que a largura do casco de uma tartaruga siga uma distribuição uniforme com largura mínima de 2 polegadas e largura máxima de 6 polegadas.

Ou seja, se selecionarmos uma tartaruga aleatoriamente e medirmos a largura de seu casco, é provável que ela também tenha entre 5 e 15 centímetros de largura .

O código a seguir mostra como criar um conjunto de dados em R contendo as medidas das larguras da carapaça de 1.000 tartarugas, distribuídas uniformemente entre 2 e 6 polegadas:

 #make this example reproducible
set. seeds (0)

#create random variable with sample size of 1000 that is uniformly distributed
data <- runif(n=1000, min=2, max=6)

#create histogram to visualize distribution of turtle shell widths
hist(data, col=' steelblue ', main=' Histogram of Turtle Shell Widths ')

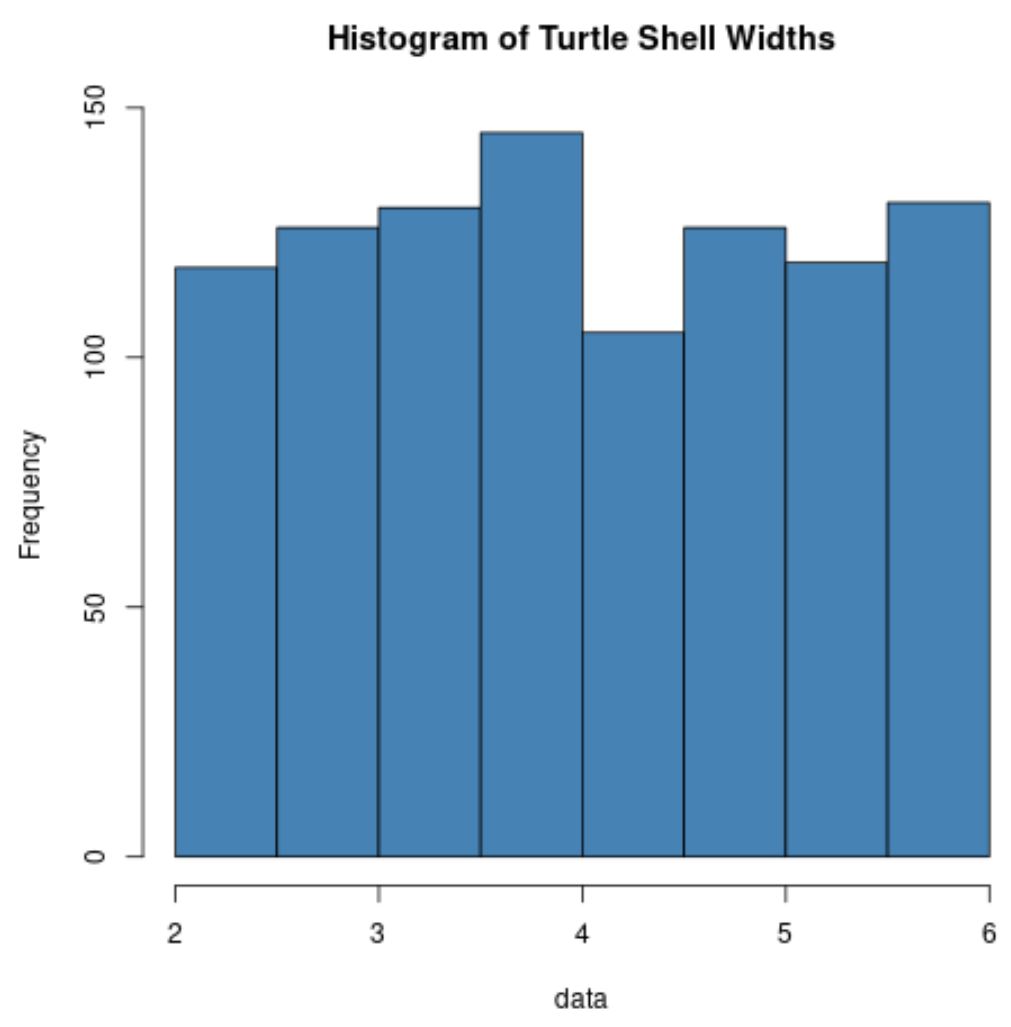
Observe que a distribuição das larguras dos cascos das tartarugas normalmente não é distribuída.

Agora imagine que pegamos amostras aleatórias repetidas de 5 tartarugas desta população e medimos a média da amostra repetidamente.

O código a seguir mostra como fazer esse processo em R e criar um histograma para visualizar a distribuição das médias amostrais:

 #create empty vector to hold sample means
sample5 <- c()

#take 1,000 random samples of size n=5
n = 1000
for (i in 1:n){
sample5[i] = mean(sample(data, 5, replace= TRUE ))
}

#calculate mean and standard deviation of sample means
mean(sample5)

[1] 4.008103

sd(sample5)

[1] 0.5171083 

#create histogram to visualize sampling distribution of sample means
hist(sample5, col = ' steelblue ', xlab=' Turtle Shell Width ', main=' Sample size = 5 ') 

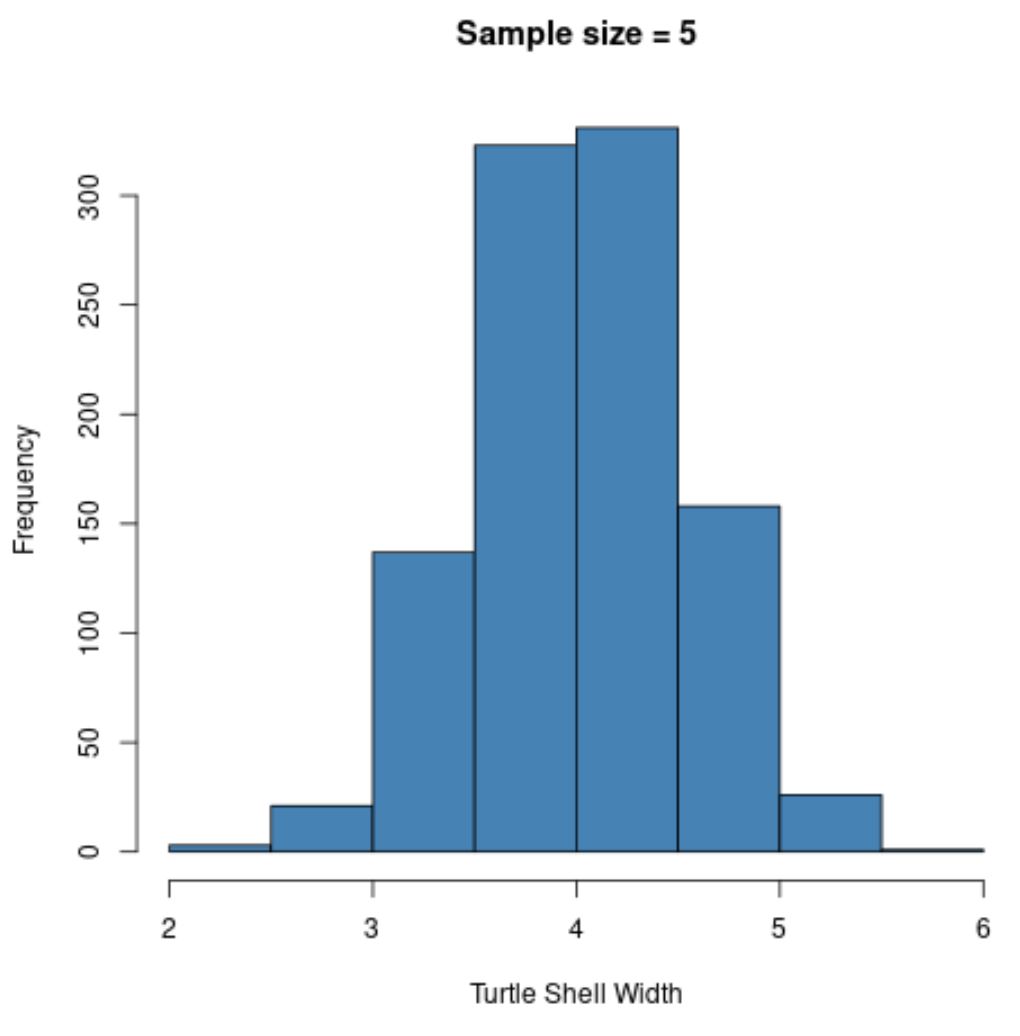
Observe que a distribuição amostral das médias amostrais parece distribuída normalmente, embora a distribuição da qual as amostras vieram não tenha sido normalmente distribuída.

Observe também a média amostral e o desvio padrão amostral para esta distribuição amostral:

• x̄ : 4,008
• s : 0,517

Agora suponha que aumentamos o tamanho da amostra que usamos de n=5 para n=30 e recriamos o histograma das médias amostrais:

 #create empty vector to hold sample means
sample30 <- c()

#take 1,000 random samples of size n=30
n = 1000
for (i in 1:n){
sample30[i] = mean(sample(data, 30, replace= TRUE ))
}

#calculate mean and standard deviation of sample means
mean(sample30)

[1] 4.000472

sd(sample30)

[1] 0.2003791

#create histogram to visualize sampling distribution of sample means
hist(sample30, col = ' steelblue ', xlab=' Turtle Shell Width ', main=' Sample size = 30 ') 

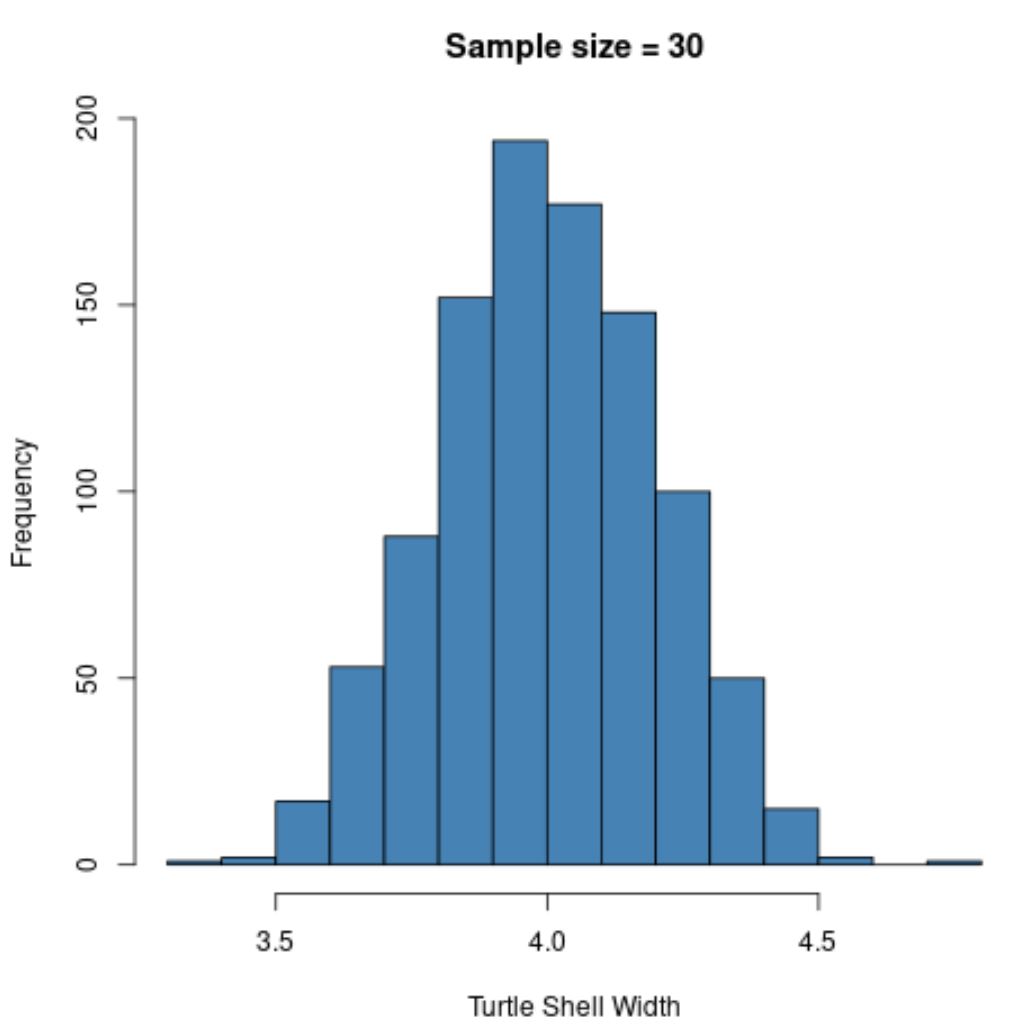
A distribuição amostral é novamente distribuída normalmente , mas o desvio padrão amostral é ainda menor:

• s : 0,200

Isso ocorre porque usamos um tamanho amostral maior (n=30) em comparação ao exemplo anterior (n=5), portanto o desvio padrão das médias amostrais é ainda menor.

Se continuarmos a usar amostras cada vez maiores, descobriremos que o desvio padrão da amostra se torna cada vez menor.

Isso ilustra o teorema do limite central na prática.

Recursos adicionais

Os seguintes recursos fornecem informações adicionais sobre o teorema do limite central:

Uma introdução ao teorema do limite central
Calculadora do Teorema do Limite Central
5 exemplos de uso do teorema do limite central na vida real