Como aplicar o teorema do limite central no excel

O teorema do limite central afirma que a distribuição amostral de uma média amostral é aproximadamente normal se o tamanho da amostra for grande o suficiente, mesmo que a distribuição populacional não seja normal .

O teorema do limite central também afirma que a distribuição amostral terá as seguintes propriedades:

1. A média da distribuição amostral será igual à média da distribuição populacional:

x = µ

2. O desvio padrão da distribuição amostral será igual ao desvio padrão da população dividido pelo tamanho da amostra:

s = σ/ √n

Neste tutorial explicamos como aplicar o teorema do limite central no Excel a uma determinada distribuição.

Aplicando o Teorema do Limite Central no Excel

Suponha que temos uma distribuição com média 8 e desvio padrão 4 . Podemos usar as seguintes fórmulas no Excel para encontrar a média e o desvio padrão da distribuição amostral com um tamanho de amostra de 15 :

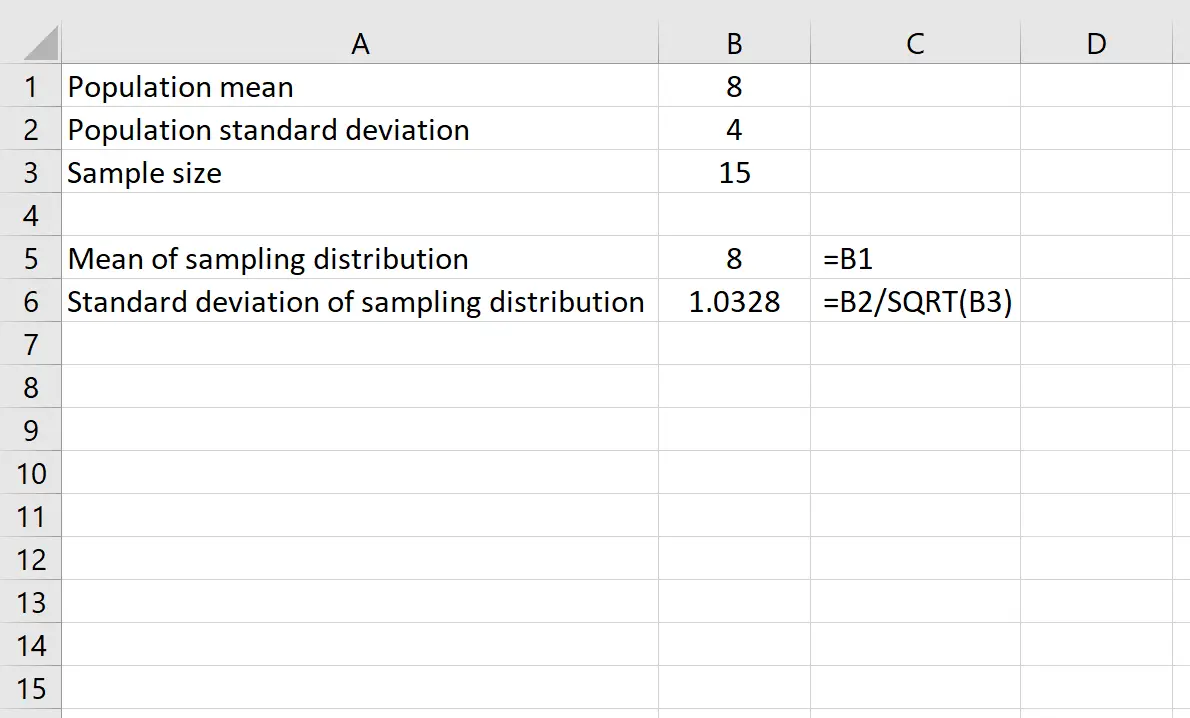
A média da distribuição amostral é simplesmente igual à média da distribuição populacional, que é 8 .

O desvio padrão da distribuição amostral é igual ao desvio padrão da população dividido pelo tamanho da amostra, ou: 4 /√15 = 1,0328 .

Também podemos usar o teorema do limite central para responder questões sobre probabilidade. Por exemplo, se uma determinada população tem uma média de 8 e um desvio padrão de 4 , qual é a probabilidade de que uma determinada amostra de tamanho 15   tem média menor ou igual a 7 ?

Para responder a esta pergunta, podemos usar a função NORM.DIST() no Excel, que utiliza a seguinte sintaxe:

DIST.NORM(x, média, desvio_padrão, cumulativo)

Ouro:

• x: amostra significa que você deseja testar
• média: média esperada da distribuição amostral
• standard_dev: desvio padrão esperado da distribuição amostral
• cumulativo: TRUE retorna o valor CDF normal; FALSE retorna o valor do PDF normal. No nosso caso, sempre usaremos TRUE.

Esta função retornará a probabilidade de que a média da amostra seja menor ou igual a um determinado valor.

Aqui está a fórmula que usaríamos neste exemplo:

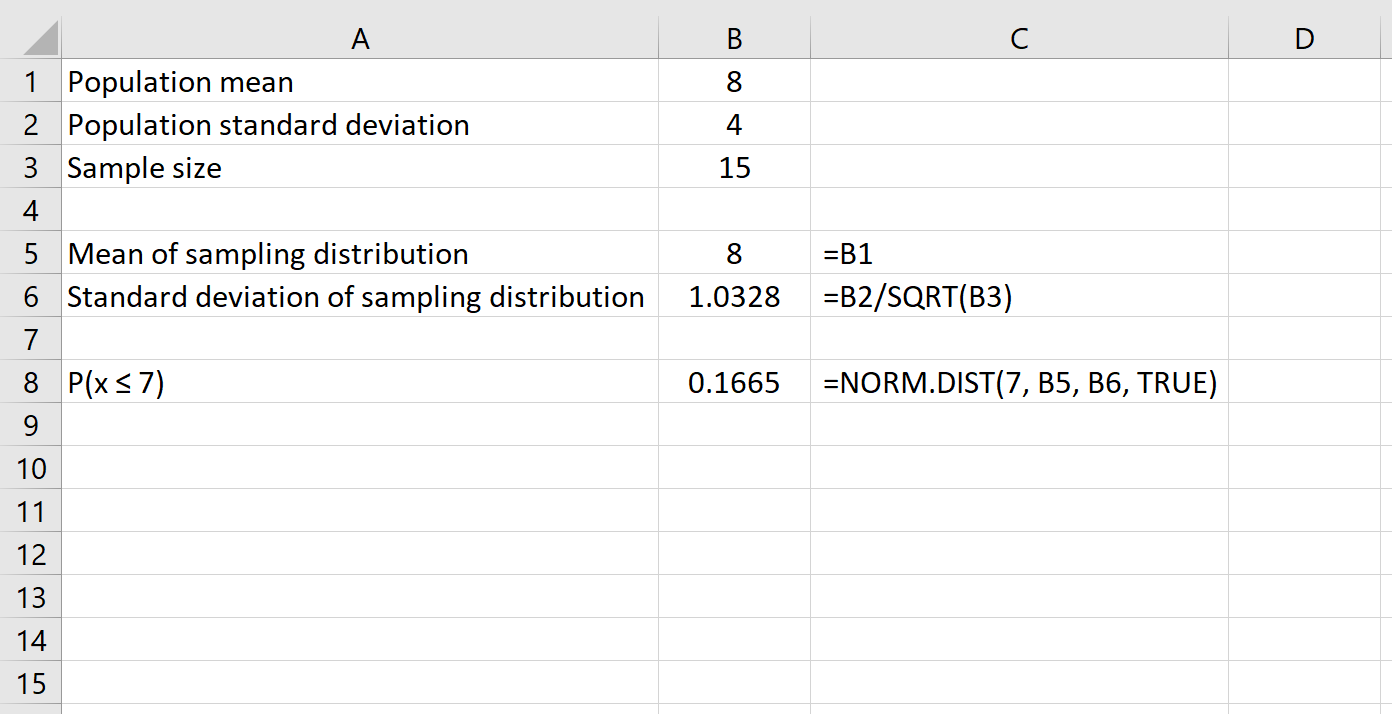
Isso nos diz que para uma população com média 8 e desvio padrão 4 , a probabilidade de que uma determinada amostra de tamanho 15   tem média menor ou igual a 7 ou 0,1665 .

Também podemos encontrar a probabilidade de que um determinado tamanho de amostra tenha uma média maior que um determinado número simplesmente usando a fórmula 1 – NORM.DIST() .

Por exemplo, a fórmula a seguir mostra como determinar a probabilidade de que um determinado tamanho de amostra de 15 tenha uma média superior a 7:

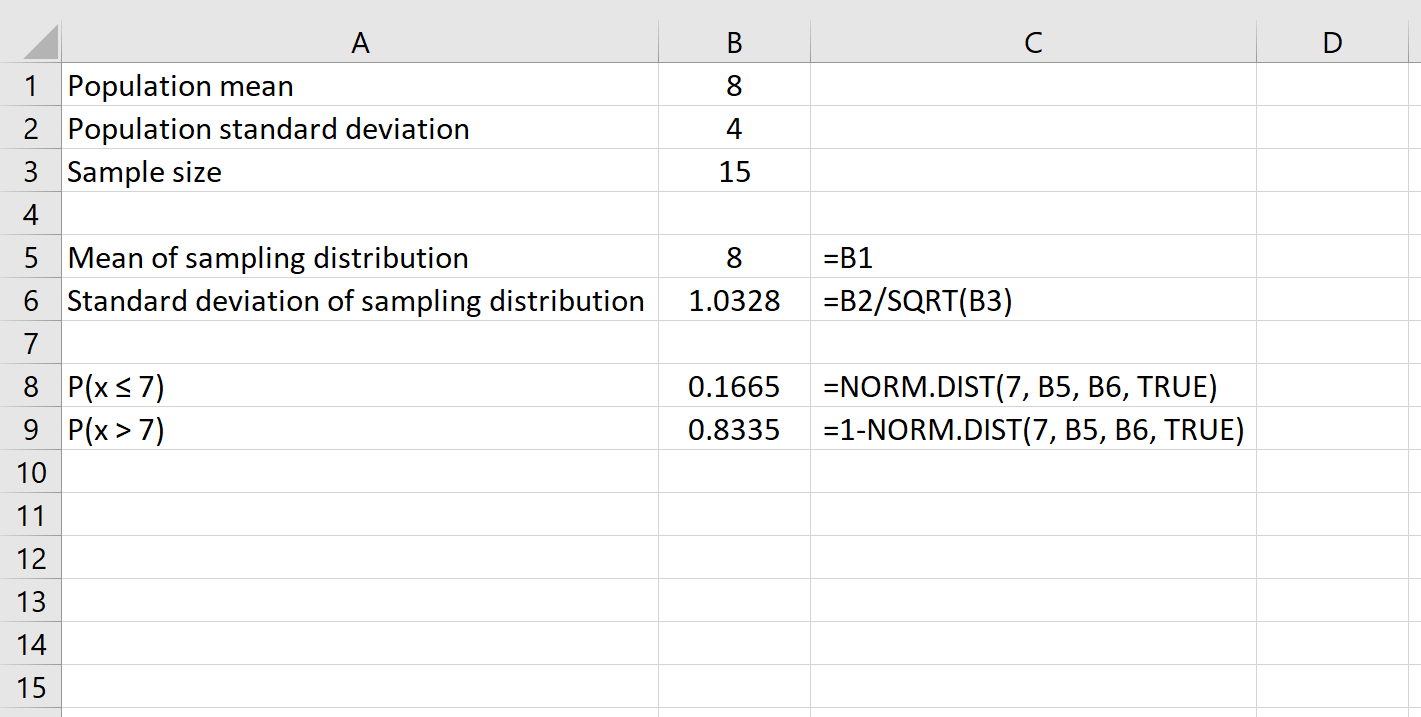
Finalmente, podemos encontrar a probabilidade de que um determinado tamanho de amostra tenha uma média entre dois números usando a fórmula NORM.DIST(número maior) – NORM.DIST(número menor) .

Por exemplo, a fórmula a seguir mostra como encontrar a probabilidade de que um determinado tamanho de amostra de 15 tenha uma média entre 7 e 9:

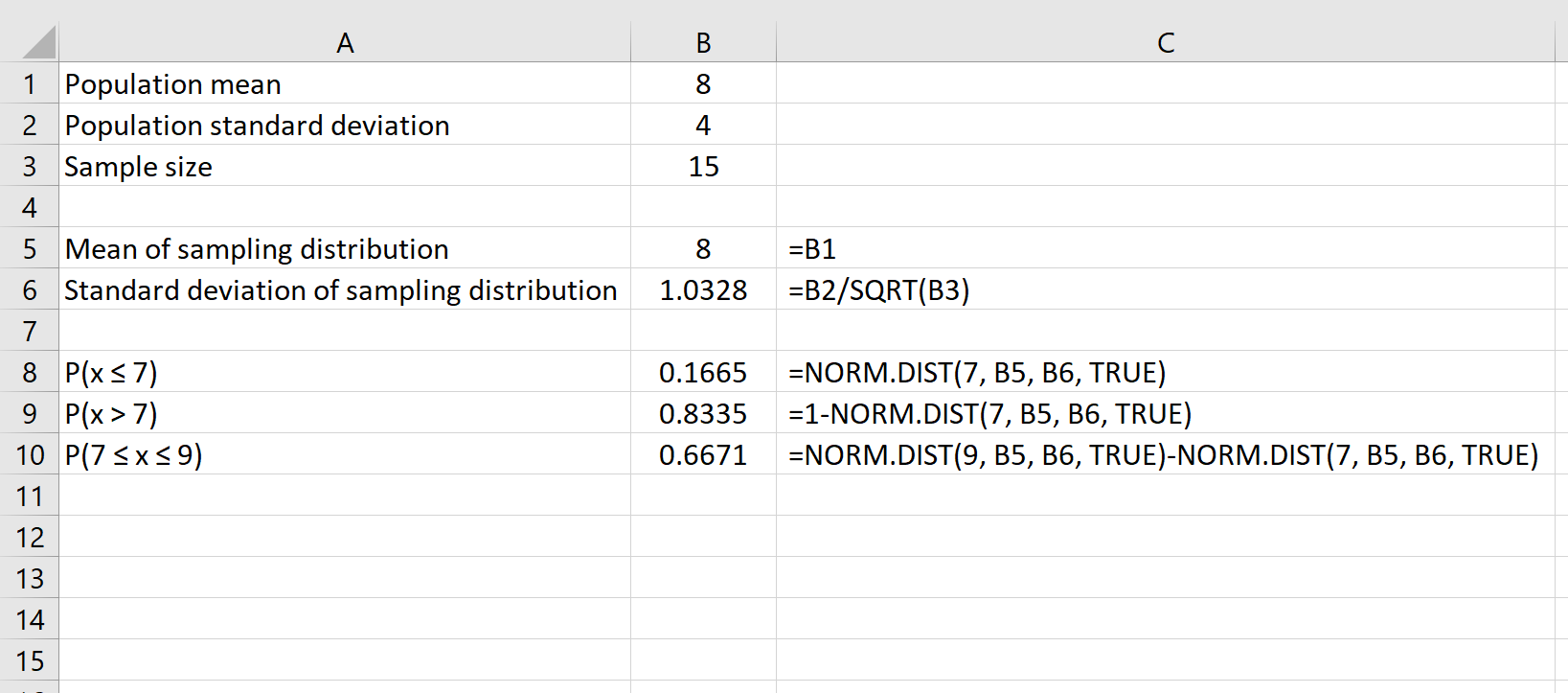
Recursos adicionais

Calculadora do Teorema do Limite Central
Como aplicar a regra prática no Excel
Como criar uma curva em forma de sino no Excel