Como aplicar o teorema do limite central na calculadora ti-84
O teorema do limite central afirma que a distribuição amostral de uma média amostral é aproximadamente normal se o tamanho da amostra for grande o suficiente, mesmo que a distribuição populacional não seja normal.
O teorema do limite central também afirma que a distribuição amostral terá as seguintes propriedades:
1. A média da distribuição amostral será igual à média da distribuição populacional:
x = µ
2. O desvio padrão da distribuição amostral será igual ao desvio padrão da população dividido pelo tamanho da amostra:
s = σ/ √n
Para encontrar as probabilidades relacionadas à média amostral em uma calculadora TI-84, podemos usar a função normalcdf() com a seguinte sintaxe:
normalcdf (lower value, upper value, x , s/√ n )
Ouro:
- x : média amostral
- s : desvio padrão da amostra
- n : tamanho da amostra
Para acessar esta função em uma calculadora TI-84, simplesmente pressione 2nd , pressione VARS e vá até normalcdf ( e pressione ENTER .
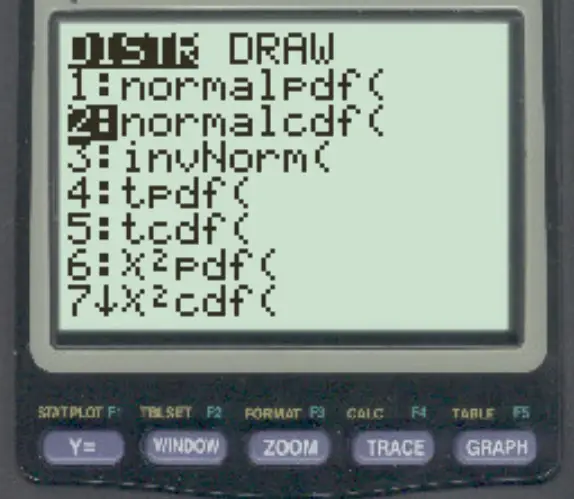
Os exemplos a seguir mostram como usar esta função na prática.
Exemplo 1: Encontre a probabilidade entre dois valores
Uma distribuição tem média de 70 e desvio padrão de 7. Se selecionarmos uma amostra aleatória de tamanho n = 35, encontre a probabilidade de que a média da amostra esteja entre 68 e 72.
Podemos usar a seguinte sintaxe na TI-84:
normalcdf (68, 72, 70, 7/√ 35 )
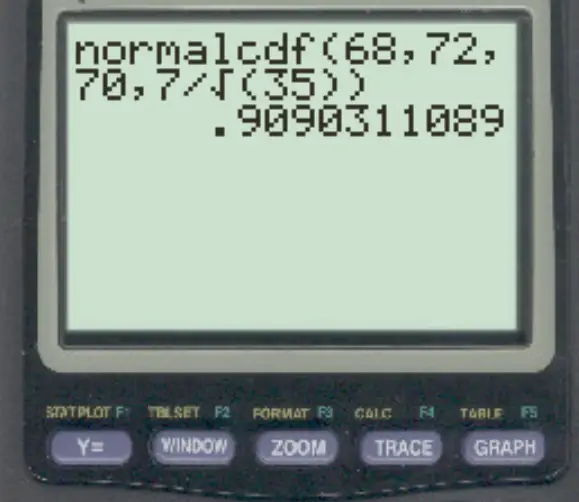
A probabilidade de a média amostral estar entre 68 e 72 é 0,909 .
Exemplo 2: Encontrando uma probabilidade maior que um valor
Uma distribuição tem média de 50 e desvio padrão de 4. Se selecionarmos uma amostra aleatória de tamanho n = 30, encontre a probabilidade de que a média da amostra seja maior que 48.
Podemos usar a seguinte sintaxe na TI-84:
normalcdf (48, E99, 50, 4/√ 30 )
Nota: Você pode acessar o símbolo “E” pressionando 2 e, em seguida, pressionando o botão , .
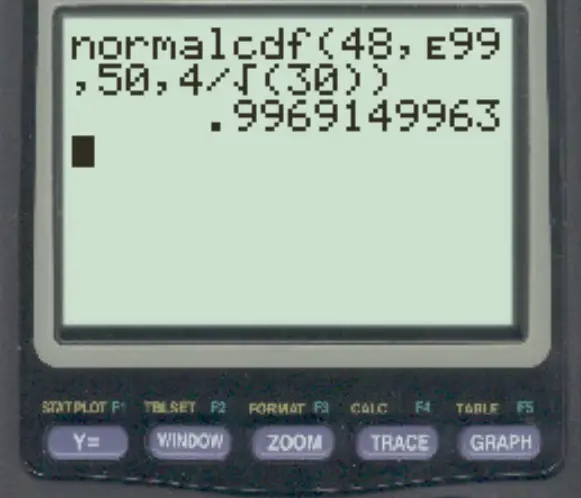
A probabilidade de a média amostral ser maior que 48 é 0,9969 .
Exemplo 3: Encontrando uma probabilidade menor que um valor
Uma distribuição tem média 20 e desvio padrão 3. Se selecionarmos uma amostra aleatória de tamanho n = 40, encontre a probabilidade de que a média da amostra seja menor que 19.
Podemos usar a seguinte sintaxe na TI-84:
normalcdf (-E99, 19, 20, 3/√ 40 )
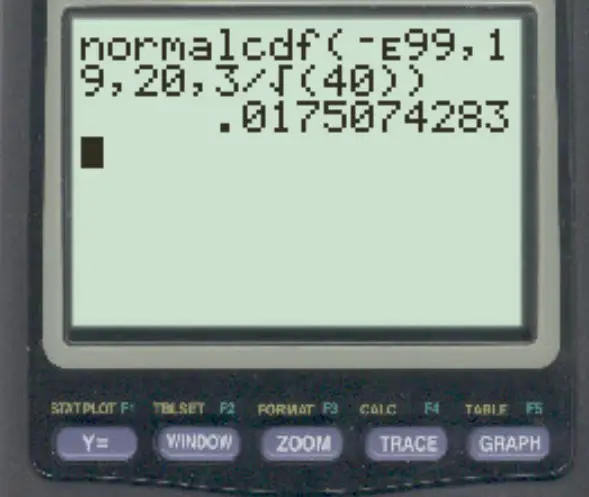
A probabilidade de a média amostral ser inferior a 19 é 0,0175 .
Recursos adicionais
Uma introdução ao teorema do limite central
Calculadora do Teorema do Limite Central
Como Aplicar o Teorema do Limite Central no Excel
Teorema do limite central: as quatro condições a serem cumpridas