Teste de bartlett para homogeneidade de variâncias (definição e exemplo)

O teste de Bartlett é um teste estatístico usado para determinar se as variações entre vários grupos são iguais ou não.

Muitos testes estatísticos (como uma ANOVA unidirecional ) assumem que as variâncias são iguais entre as amostras. O teste de Bartlett pode ser usado para verificar esta hipótese.

As etapas a seguir explicam como realizar o teste de Bartlett.

Nota: Não confunda este teste como teste de esfericidade de Bartlett , que é usado para comparar uma matriz de correlação observada com a matriz identidade.

Etapas para realizar o teste Bartlett

O teste de Bartlett usa as seguintes hipóteses nulas e alternativas:

H ₀ : A variância entre cada grupo é igual.

_HA : Pelo menos um grupo tem uma variância que não é igual aos outros.

A estatística de teste pode ser calculada da seguinte forma:

B = (nk)lns ² – Σ(n _j -1)lns _j ² / c

Ouro:

• n: o número total de observações em todos os grupos
• k: O número total de grupos
• ln: Isso significa “log natural”
• s ² : A variação agrupada
• n _j : O número de observações no grupo j
• s _j ² : A variância do grupo j

E onde é calculado da seguinte forma:

• c = 1 + (1/3(k-1))*(Σ(1/(n _j -1)) – (1/(nk))

Esta estatística de teste segue uma distribuição qui-quadrado com k-1 graus de liberdade. Em outras palavras, B ~ X ² (k-1).

Se o valor p que corresponde à estatística de teste estiver abaixo de um certo nível de significância (como α = 0,05), então podemos rejeitar a hipótese nula e concluir que nem todos os grupos têm a mesma variância.

Exemplo: teste de Bartlett

Suponha que um professor queira saber se três técnicas de estudo diferentes levam a notas médias diferentes nos exames.

Ela designa aleatoriamente 10 alunos para usar cada técnica durante uma semana e depois dá a cada aluno um exame de igual dificuldade.

Os resultados dos exames dos 30 alunos são apresentados abaixo:

A professora deseja realizar uma ANOVA unidirecional para verificar se as três técnicas levam a notas médias diferentes no exame, mas ela deve primeiro realizar o teste de Bartlett para verificar se os três grupos têm variâncias iguais.

É tedioso realizar o teste de Bartlett manualmente, então inseriremos os seguintes valores de dados na calculadora do teste de Bartlett :

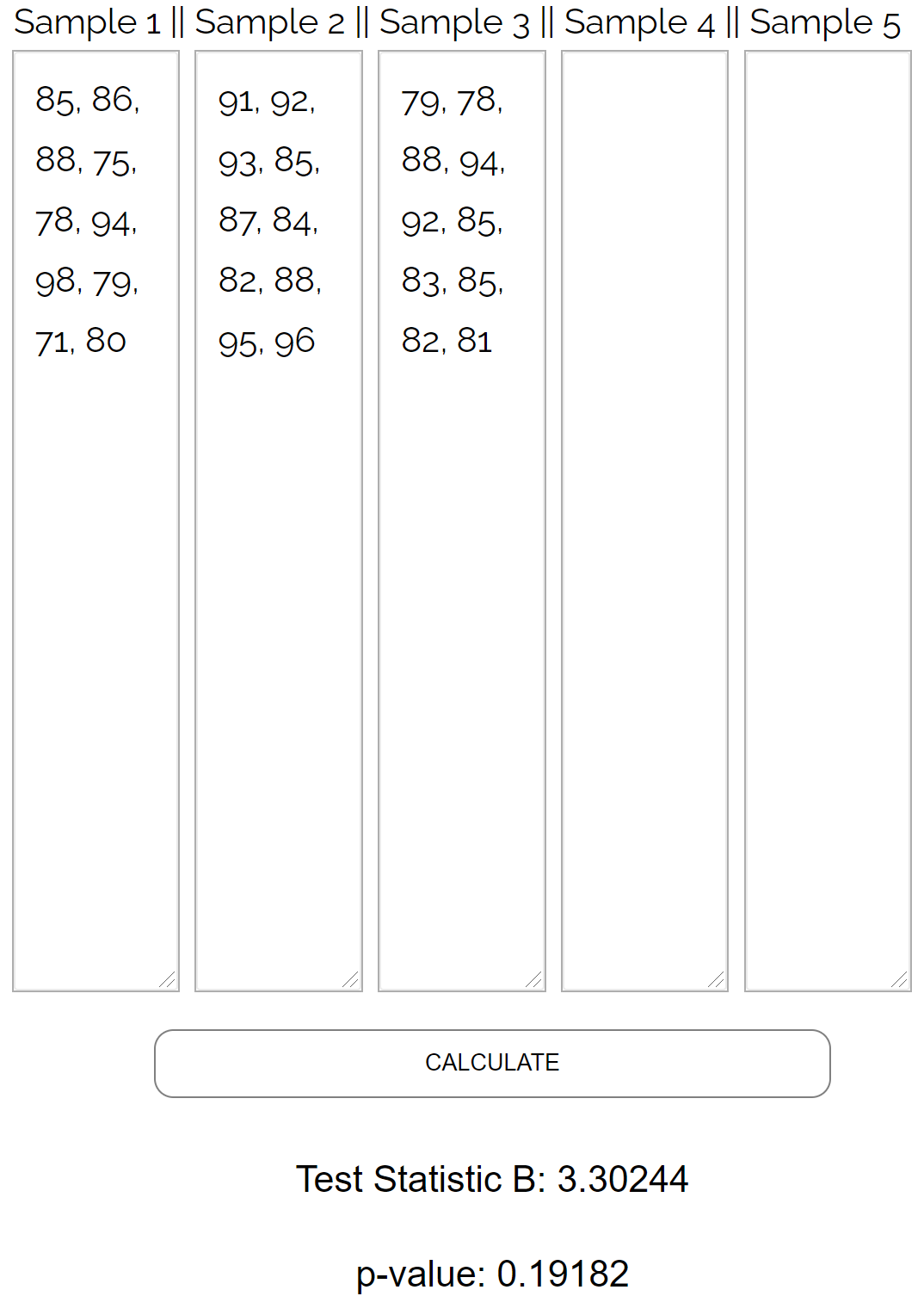
O teste retorna os seguintes resultados:

• Estatística de teste B : 3,30244
• Valor P: 0,19182

Como o valor p não é inferior a 0,05, o professor não rejeitará a hipótese nula. Por outras palavras, ela não tem provas suficientes para dizer que os três grupos têm lacunas diferentes.

Assim, ela pode proceder à realização da ANOVA unidirecional.

Recursos adicionais

Como realizar o teste de Bartlett em R (passo a passo)
Como realizar o teste Bartlett em Python (passo a passo)