O que é um teste alimentar? (explicação e exemplo)

Um teste de Chow é um teste estatístico desenvolvido pelo economista Gregory Chow que é usado para testar se os coeficientes de dois modelos de regressão diferentes em conjuntos de dados diferentes são iguais.

O teste de Chow é normalmente usado no campo da econometria com dados de séries temporais para determinar se há uma quebra estrutural nos dados em um determinado momento.

Por exemplo, considere o seguinte gráfico de dispersão:

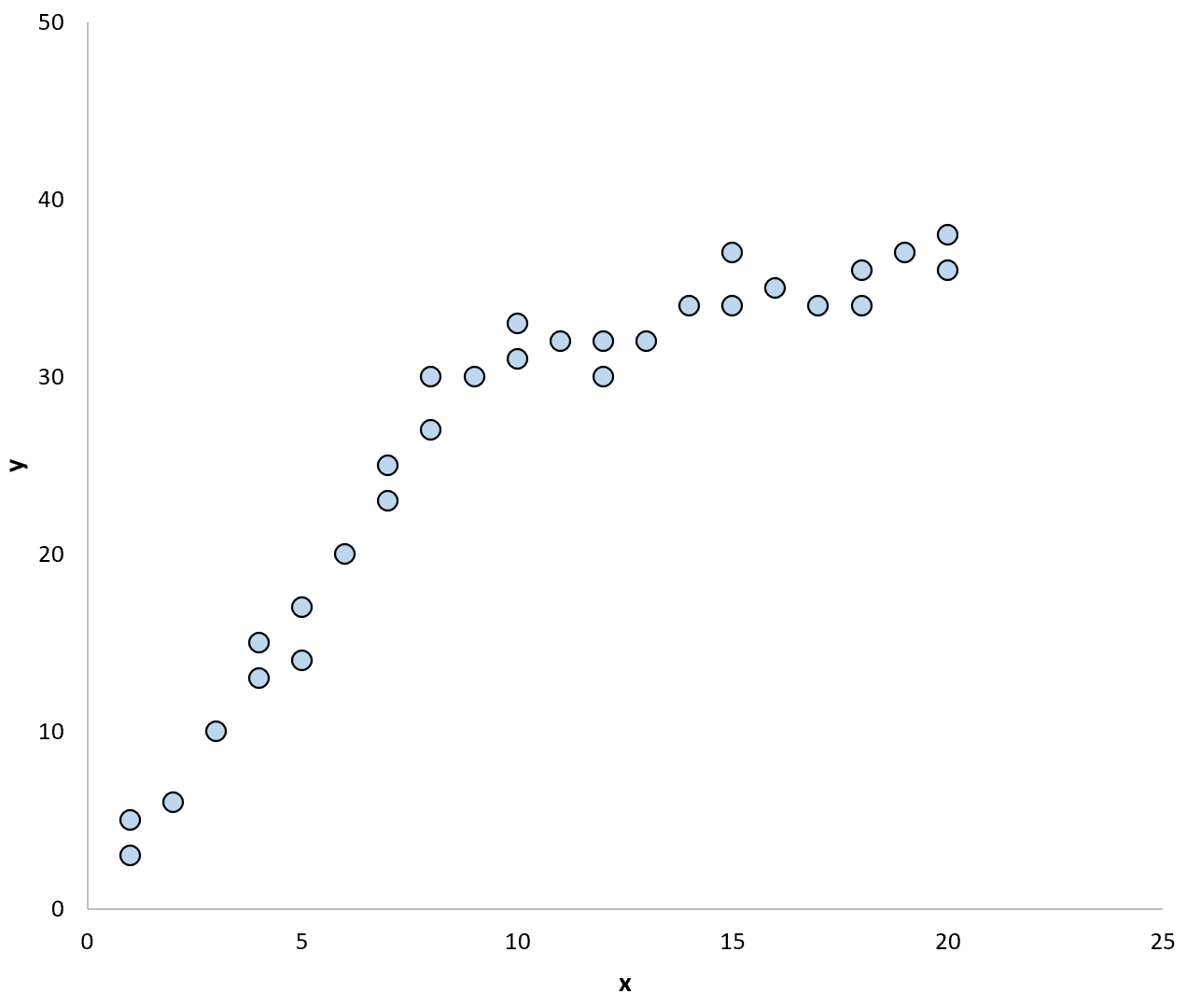
Se usássemos uma linha de regressão para resumir o modelo nos dados, poderia ter a seguinte aparência:

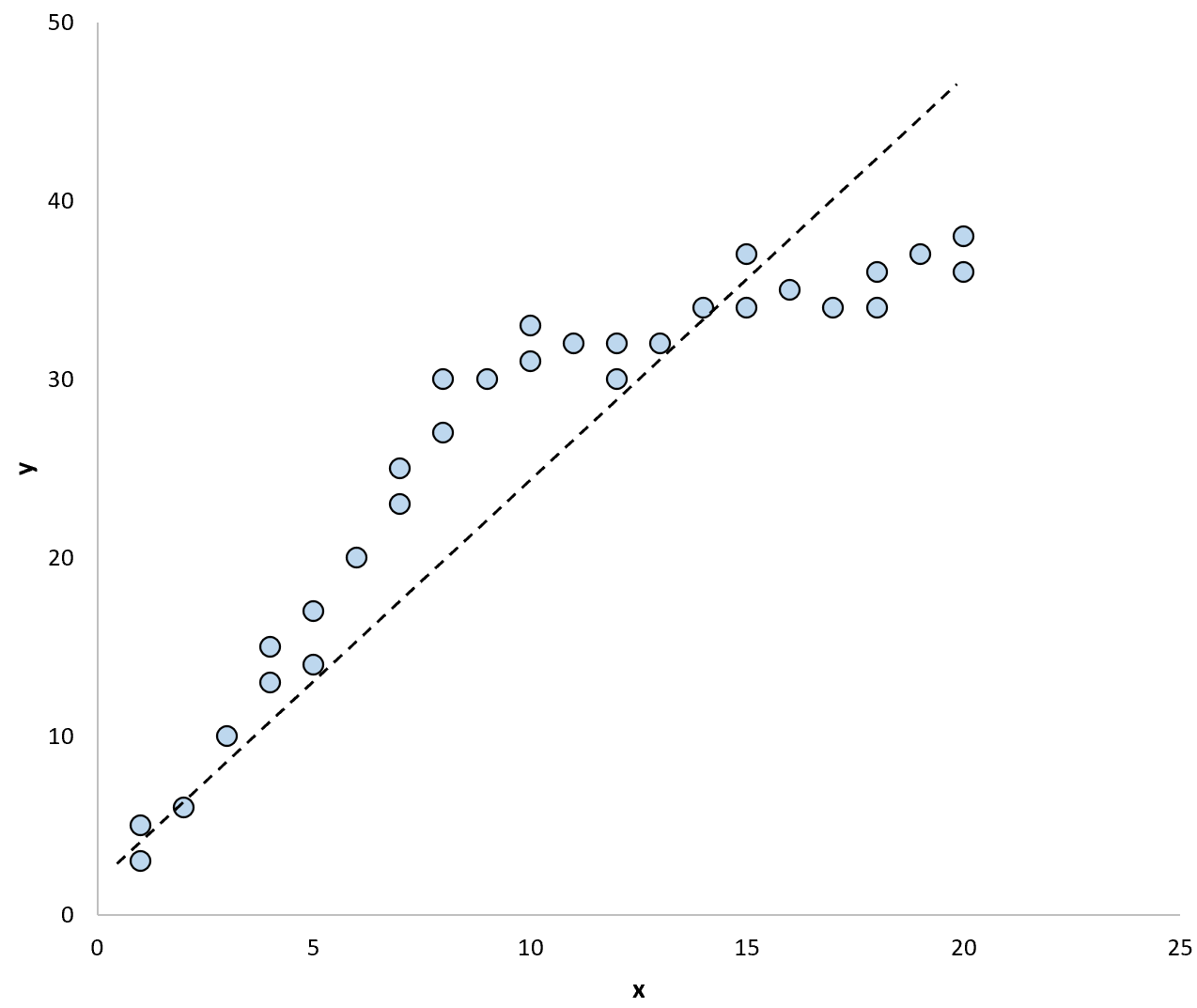
E se usássemos duas linhas de regressão separadas para resumir o modelo nos dados, poderia ficar assim:

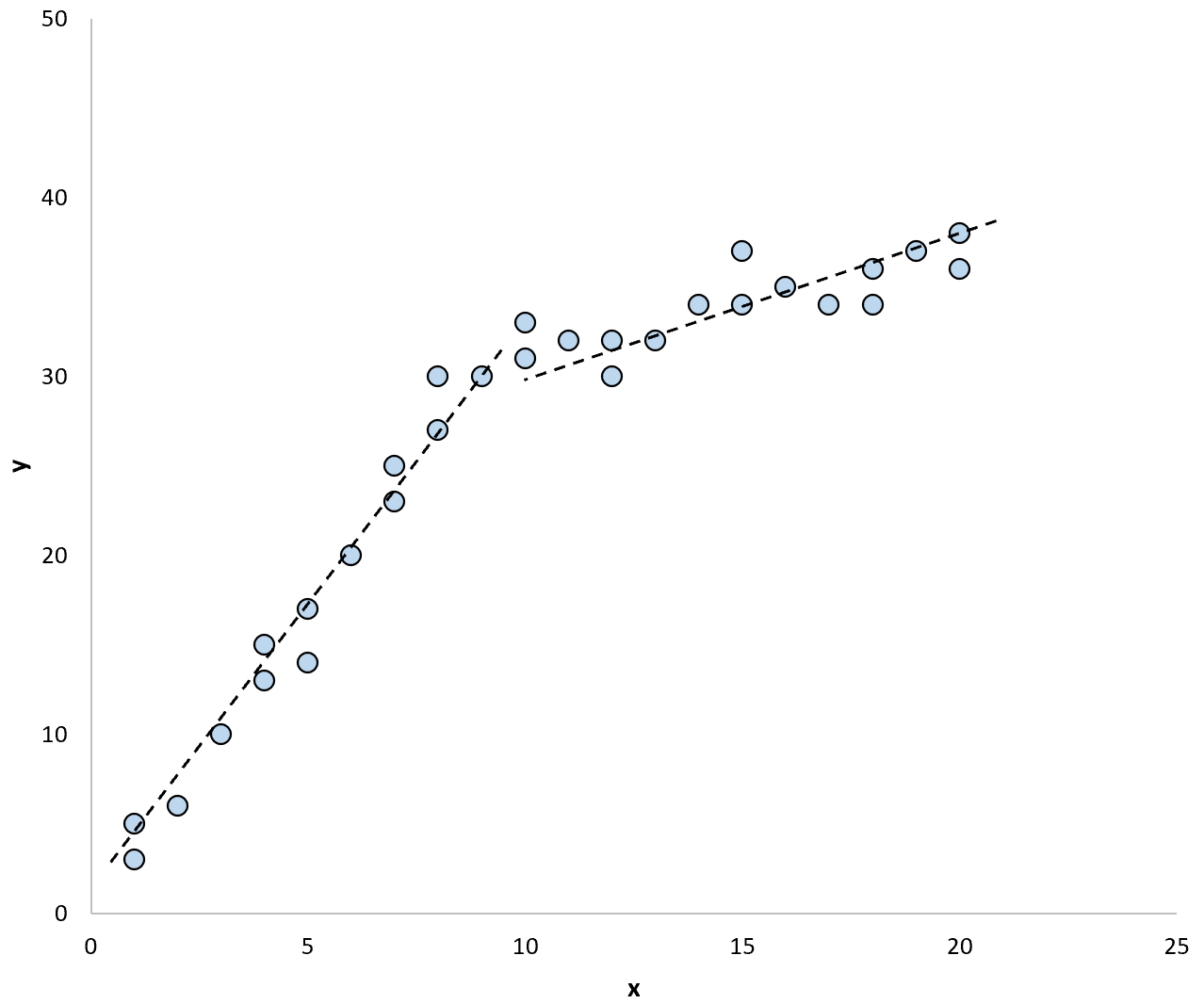
O teste de Chow permite testar se os coeficientes de regressão de cada linha de regressão são iguais ou não.

Se o teste determinar que os coeficientes não são iguais entre as linhas de regressão, isso significa que há evidências significativas de uma quebra estrutural nos dados. Por outras palavras, a tendência dos dados é muito diferente antes e depois deste ponto de ruptura estrutural.

Quando usar o teste Chow

Os exemplos a seguir ilustram situações em que você pode querer realizar um teste Chow:

1. Determine se os preços das ações variam em taxas diferentes antes e depois de uma eleição.

2. Determinar se os preços das casas mudam antes e depois de uma alteração na taxa de juros.

3. Determinar se o lucro médio das empresas públicas é diferente antes e depois da adopção de uma nova lei fiscal.

Em cada situação, poderíamos usar um teste de Chow para determinar se existe um ponto de ruptura estrutural nos dados em um determinado momento.

Etapas para realizar um teste de comida

Podemos usar as etapas a seguir para realizar um teste de Chow.

Etapa 1: Defina as hipóteses nula e alternativa.

Suponha que ajustemos o seguinte modelo de regressão a todo o nosso conjunto de dados:

• y _t = a + bx _1t + cx _t2 + ε

A seguir, suponha que dividamos nossos dados em dois grupos com base em um ponto de interrupção estrutural e ajustemos os seguintes modelos de regressão a cada grupo:

• y _t = a ₁ + b ₁ x _1t + c ₁ x _t2 + ε
• y _t = a ₂ + b ₂ x _1t + c ₂ x _t2 + ε

Usaríamos as seguintes hipóteses nulas e alternativas para o teste de Chow:

• Nulo (H ₀ ): a ₁ = a ₂ , b ₁ = b ₂ e c ₁ = c ₂
• Alternativa ( _HA ): Pelo menos uma das comparações em Nulo não é igual.

Se rejeitarmos a hipótese nula, teremos provas suficientes para dizer que existe um ponto de ruptura estrutural nos dados e que duas linhas de regressão podem ajustar-se melhor aos dados do que uma.

Se não conseguirmos rejeitar a hipótese nula, não teremos provas suficientes para dizer que existe um ponto de ruptura estrutural nos dados. Nesse caso, dizemos que as linhas de regressão podem ser “agrupadas” em uma única linha de regressão que represente suficientemente bem o padrão dos dados.

Etapa 2: Calcule a estatística de teste.

Se definirmos os seguintes termos:

• S _T : A soma dos quadrados dos resíduos dos dados totais
• S ₁ , S ₂ : soma dos quadrados dos resíduos de cada grupo
• N ₁ , N ₂ : O número de observações em cada grupo
• k: O número de parâmetros

Podemos então dizer que a estatística do teste Chow é:

Estatística do teste Chow = [(S _T – (S ₁ +S ₂ ))/k] / [(S ₁ +S ₂ )/ (N ₁ +N ₂ -2k)]

Esta estatística de teste segue a distribuição F com k e e N ₁ +N ₂ -2k graus de liberdade.

Etapa 3: Rejeite ou não rejeite a hipótese nula.

Se o valor p associado a esta estatística de teste estiver abaixo de um certo nível de significância , podemos rejeitar a hipótese nula e concluir que há um ponto de quebra estrutural nos dados.

Felizmente, a maioria dos softwares estatísticos é capaz de realizar um teste de Chow, portanto você provavelmente nunca terá que realizar o teste manualmente.

Exemplo de realização de um teste Chow

Consulte este tutorial para ver um exemplo passo a passo de como realizar um teste Chow para um determinado conjunto de dados em R.

Notas de teste de comida

Aqui estão algumas notas que você deve ter em mente sobre o teste Chow:

1. O teste assume que os resíduos dos modelos de regressão são distribuídos de forma independente e idêntica a partir de uma distribuição normal com variância desconhecida.

2. O teste de Chow só deve ser utilizado quando a ruptura estrutural que se deseja testar ocorrer em um momento conhecido . Em outras palavras, o teste não deve ser utilizado repetidamente para determinar se um determinado momento pode ser considerado uma ruptura estrutural.