Como realizar um teste de correlação em r (com exemplos)

Uma forma de quantificar a relação entre duas variáveis é utilizar o coeficiente de correlação de Pearson , que é uma medida da associação linear entre duas variáveis .

Sempre assume um valor entre -1 e 1 onde:

• -1 indica uma correlação linear perfeitamente negativa entre duas variáveis
• 0 indica nenhuma correlação linear entre duas variáveis
• 1 indica uma correlação linear perfeitamente positiva entre duas variáveis

Para determinar se um coeficiente de correlação é estatisticamente significativo, você pode calcular a pontuação t e o valor p correspondentes.

A fórmula para calcular o escore t de um coeficiente de correlação (r) é:

t = r * √ n-2 / √ 1-r ²

O valor p é calculado como o valor p bicaudal correspondente para a distribuição t com n-2 graus de liberdade.

Exemplo: teste de correlação em R

Para determinar se o coeficiente de correlação entre duas variáveis é estatisticamente significativo, você pode realizar um teste de correlação em R usando a seguinte sintaxe:

cor.test(x, y, método=c(“pearson”, “kendall”, “lanceiro”))

Ouro:

• x, y: vetores de dados digitais.
• método: Método utilizado para calcular a correlação entre dois vetores. O padrão é “Pearson”.

Por exemplo, suponha que temos os dois vetores a seguir em R:

 x <- c(2, 3, 3, 5, 6, 9, 14, 15, 19, 21, 22, 23)
y <- c(23, 24, 24, 23, 17, 28, 38, 34, 35, 39, 41, 43)

Antes de realizar um teste de correlação entre as duas variáveis, podemos criar um gráfico de dispersão rápido para visualizar sua relação:

 #create scatterplot
plot(x, y, pch= 16 )

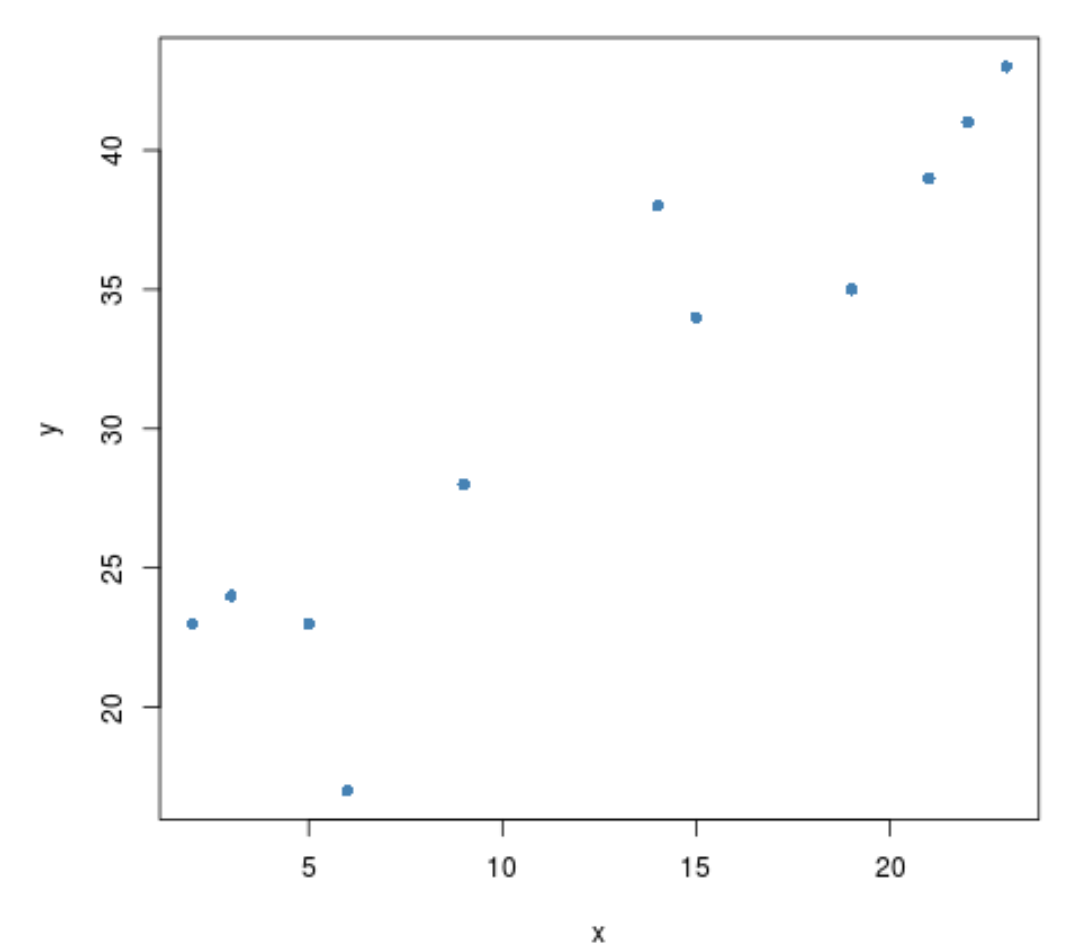
Parece haver uma correlação positiva entre as duas variáveis. Ou seja, à medida que um aumenta, o outro tende a aumentar também.

Para ver se esta correlação é estatisticamente significativa, podemos realizar um teste de correlação:

 #perform correlation test between the two vectors
cor.test(x, y)

	Pearson's product-moment correlation

data: x and y
t = 7.8756, df = 10, p-value = 1.35e-05
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.7575203 0.9799783
sample estimates:
      horn 
0.9279869

O coeficiente de correlação entre os dois vetores é 0,9279869 .

A estatística de teste é 7,8756 e o valor p correspondente é 1,35e-05 .

Dado que este valor é inferior a 0,05, temos evidências suficientes para afirmar que a correlação entre as duas variáveis é estatisticamente significativa.

Recursos adicionais

Os tutoriais a seguir fornecem informações adicionais sobre coeficientes de correlação:

Uma introdução ao coeficiente de correlação de Pearson
O que é considerado uma correlação “forte”?
As cinco hipóteses da correlação de Pearson