Como realizar o teste de dunnett em r

Um teste post hoc é um tipo de teste realizado após uma ANOVA para determinar quais médias de grupo são estatisticamente significativamente diferentes umas das outras.

Se um dos grupos de estudo for considerado grupo controle , então devemos utilizar o teste de Dunnett como teste post-hoc.

Este tutorial explica como realizar o teste Dunnett em R.

Exemplo: teste de Dunnett em R

Suponha que um professor queira saber se duas novas técnicas de estudo têm o potencial de melhorar as notas dos seus alunos nos testes. Para testar isso, ela divide aleatoriamente sua turma de 30 alunos nos três grupos a seguir:

• Grupo controle: 10 alunos
• Novo estudo técnico 1: 10 alunos
• Novo estudo técnico 2: 10 alunos

Depois de uma semana usando a técnica de estudo atribuída, cada aluno faz o mesmo exame.

Podemos usar as seguintes etapas em R para criar um conjunto de dados, visualizar as médias do grupo, realizar uma ANOVA unidirecional e, finalmente, realizar o teste de Dunnett para determinar qual nova técnica de estudo (se houver) produz resultados diferentes em comparação com o grupo de controle .

Etapa 1: crie o conjunto de dados.

O código a seguir mostra como criar um conjunto de dados contendo os resultados dos exames de todos os 30 alunos:

 #create data frame
data <- data.frame(technique = rep (c("control", "new1", "new2"), each = 10 ),
                   score = c(76, 77, 77, 81, 82, 82, 83, 84, 85, 89,
                             81, 82, 83, 83, 83, 84, 87, 90, 92, 93,
                             77, 78, 79, 88, 89, 90, 91, 95, 95, 98))

#view first six rows of data frame
head(data)

  technical score
1 control 76
2 controls 77
3 controls 77
4 controls 81
5 controls 82
6 controls 82

Etapa 2: visualize os resultados dos exames de cada grupo.

O código a seguir mostra como produzir boxplots para visualizar a distribuição dos resultados dos exames para cada grupo:

 boxplot(score ~ technique,
        data = data,
        main = "Exam Scores by Studying Technique",
        xlab = "Studying Technique",
        ylab = "Exam Scores",
        col = "steelblue",
        border = "black")

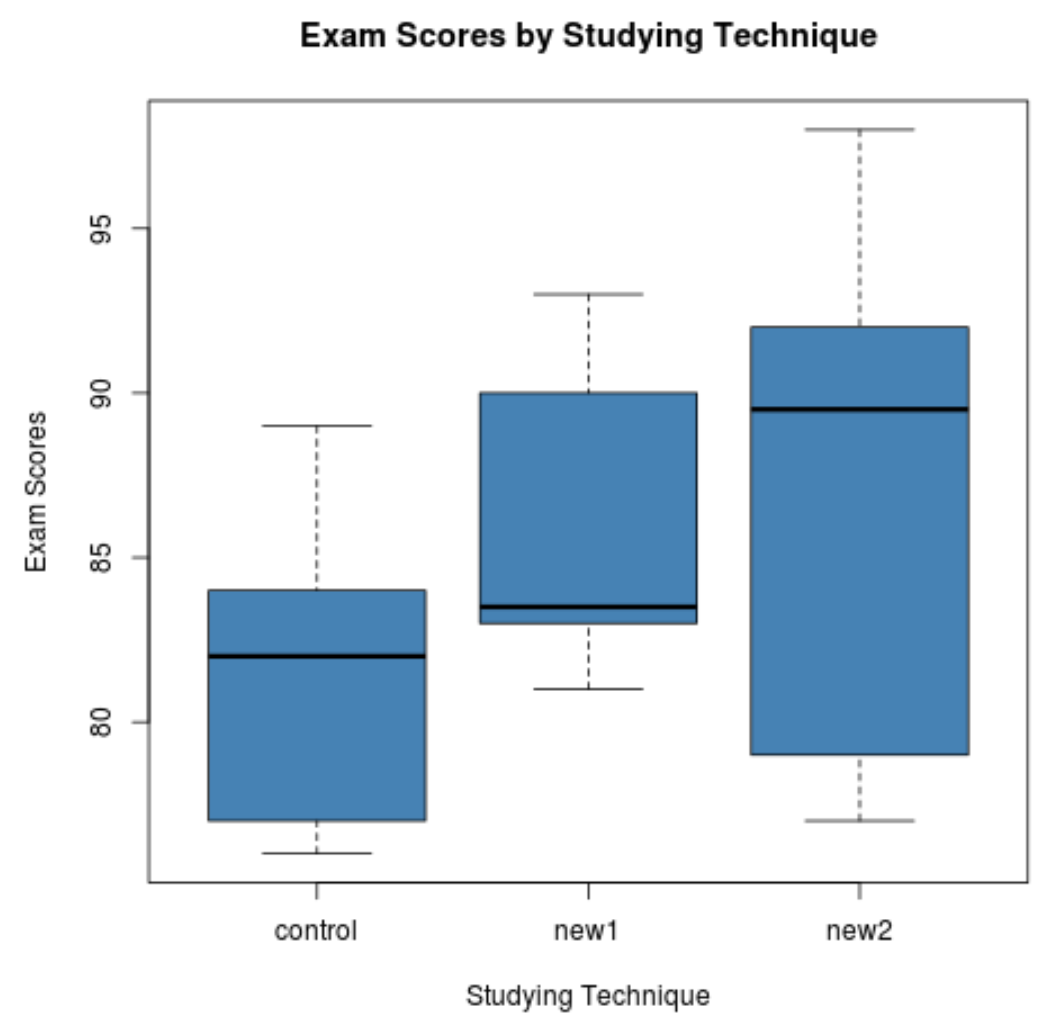
Apenas pelos box plots, podemos perceber que a distribuição das notas dos exames é muito diferente para cada técnica de estudo. Em seguida, realizaremos uma ANOVA unidirecional para determinar se essas diferenças são estatisticamente significativas.

Relacionado:Como traçar vários gráficos de caixa em um único gráfico em R

Etapa 3: execute uma ANOVA unidirecional.

O código a seguir mostra como realizar uma ANOVA unidirecional para testar as diferenças entre as pontuações médias dos exames em cada grupo:

 #fit the one-way ANOVA model
model <- aov(score ~ technique, data = data)

#view model output
summary(model)

            Df Sum Sq Mean Sq F value Pr(>F)  
technical 2 211.5 105.73 3.415 0.0476 *
Residuals 27 836.0 30.96                 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Como o valor p geral ( 0,0476 ) é inferior a 0,05, isso indica que cada grupo não tem a mesma nota média no exame. A seguir, realizaremos o teste de Dunnett para determinar qual técnica de estudo produz notas médias nos exames que diferem daquelas do grupo de controle.

Etapa 4: execute o teste de Dunnett.

Para realizar o teste Dunnett em R podemos usar a função DunnettTest() da biblioteca DescTools que utiliza a seguinte sintaxe:

Teste de Dunnett (x, g)

Ouro:

• x: um vetor numérico de valores de dados (por exemplo, resultados de exames)
• g: Um vetor que especifica os nomes dos grupos (por exemplo, técnica de estudo)

O código a seguir mostra como usar esta função em nosso exemplo:

 #load DescTools library
library(DescTools)

#perform Dunnett's Test
DunnettTest(x=data$score, g=data$technique)

  Dunnett's test for comparing several treatments with a control:  
    95% family-wise confidence level

$control
             diff lwr.ci upr.ci pval    
new1-control 4.2 -1.6071876 10.00719 0.1787    
new2-control 6.4 0.5928124 12.20719 0.0296 *  

---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1' '1.' 0.1 ' ' 1

A forma de interpretar o resultado é a seguinte:

• A diferença média nas notas dos exames entre a nova técnica de estudo 1 e o grupo de controle é de 4,2. O valor p correspondente é 0,1787 .
• A diferença média nas notas dos exames entre a nova técnica de estudo 2 e o grupo de controle é de 6,4. O valor p correspondente é 0,0296 .

Com base nos resultados, podemos perceber que o estudo da Técnica 2 é a única técnica que produz notas médias nos exames significativamente (p = 0,0296) diferentes daquelas do grupo controle.

Recursos adicionais

Uma introdução à ANOVA unidirecional
Como realizar ANOVA unidirecional em R
Como realizar o teste de Tukey em R