Como realizar o teste de scheffe no sas

Uma ANOVA unidirecional é usada para determinar se há ou não uma diferença estatisticamente significativa entre as médias de três ou mais grupos independentes.

Se o valor p geral da tabela ANOVA estiver abaixo de um certo nível de significância, então temos evidências suficientes para dizer que pelo menos uma das médias do grupo é diferente das outras.

No entanto, isso não nos diz quais grupos são diferentes uns dos outros. Isto simplesmente nos diz que nem todas as médias dos grupos são iguais.

Para saber exatamente quais grupos são diferentes entre si, precisamos realizar um teste post hoc .

Um dos testes post hoc mais comumente usados é o teste de Scheffe , que nos permite fazer comparações pareadas entre as médias de cada grupo enquanto controlamos a taxa de erro familiar .

O exemplo a seguir mostra como realizar o teste de Scheffe em R.

Exemplo: teste Scheffe em SAS

Suponha que um pesquisador recrute 30 estudantes para participar de um estudo. Os alunos são designados aleatoriamente para usar um dos três métodos de estudo para se preparar para um exame.

Podemos usar o seguinte código para criar este conjunto de dados no SAS:

 /*create dataset*/
data my_data;
    input Method $Score;
    datalines ;
At 76
At 77
At 77
At 81
At 82
At 82
At 83
At 84
At 85
At 89
B 81
B 82
B 83
B 83
B 83
B 84
B 87
B90
B92
B93
C 77
C 78
C 79
C 88
C 89
C 90
C 91
C 95
C 98
C 98
;
run ;

A seguir, usaremos proc ANOVA para realizar a ANOVA unidirecional:

 /*perform one-way ANOVA with Scheffe's post-hoc test*/
proc ANOVA data = my_data;
classMethod ;
modelScore = Method;
means Method / scheffe cldiff ;
run;

Nota : Usamos a declaração de média junto com as opções de Scheffe e Cldiff para especificar que o teste post-hoc de Scheffe deve ser realizado (com intervalos de confiança) se o valor p geral da ANOVA unidirecional for estatisticamente significativo.

Primeiramente, analisaremos a tabela ANOVA no resultado:

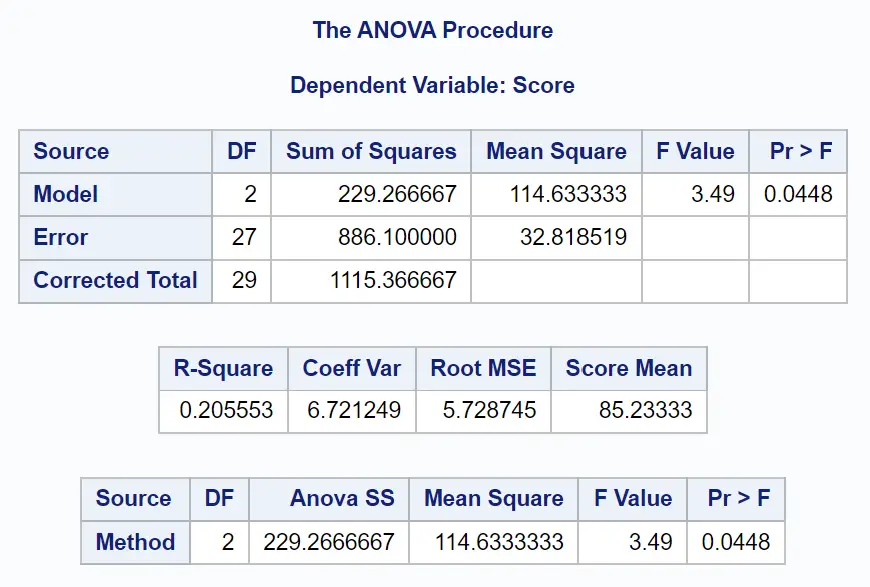
Nesta tabela podemos ver:

• Valor F geral: 3,49
• O valor p correspondente: 0,0448

Lembre-se de que uma ANOVA unidirecional usa as seguintes hipóteses nulas e alternativas:

• H ₀ : Todas as médias do grupo são iguais.
• _HA : Pelo menos a média de um grupo é diferente   descansar.

Como o valor p da tabela ANOVA (0,0448) é menor que α = 0,05, rejeitamos a hipótese nula.

Isso nos diz que a pontuação média do exame não é igual nos três métodos de estudo.

Relacionado: Como interpretar o valor F e o valor P na ANOVA

Para determinar exatamente quais médias de grupo são diferentes, precisamos consultar a tabela de resultados finais que mostra os resultados dos testes post-hoc de Scheffe:

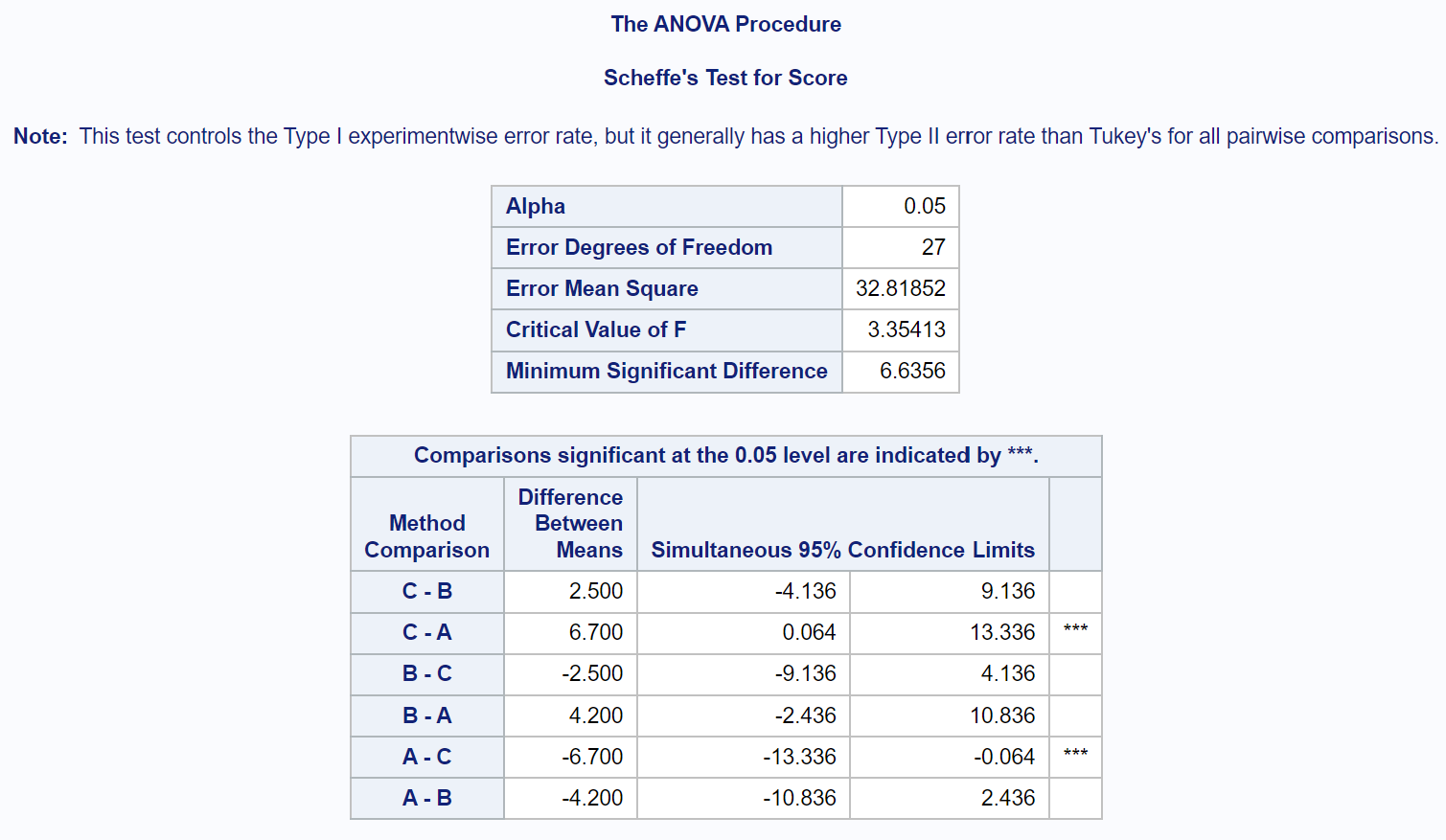
Para descobrir quais médias de grupo são diferentes, precisamos observar quais comparações de pares têm estrelas ( *** ) próximas a elas.

A tabela mostra que há uma diferença estatisticamente significativa nas notas médias dos exames entre o Grupo A e o Grupo C.

Não há diferenças estatisticamente significativas entre as médias dos demais grupos.

Especificamente, podemos ver que a diferença média nas notas dos exames entre o grupo C e o grupo A é de 6,7 .

O intervalo de confiança de 95% para a diferença nas médias entre esses grupos é [0,064, 13,336] .

Recursos adicionais

Os tutoriais a seguir fornecem informações adicionais sobre modelos ANOVA:

Um guia para usar testes post-hoc com ANOVA
Como realizar ANOVA unidirecional no SAS
Como realizar ANOVA bidirecional no SAS