Teste de hipótese para a média

By Dr. benjamim anderson Agosto 3, 2023 Estatisticas 0 Comments

Este artigo explica o que é o teste de hipótese para a média nas estatísticas. Assim, você encontrará a fórmula do teste de hipótese da média e, além disso, um exercício resolvido passo a passo.

O que é teste de hipótese para a média?

O teste de hipóteses para a média é um método estatístico usado para rejeitar ou rejeitar a hipótese nula de uma média populacional.

Mais especificamente, o teste de hipótese para a média envolve calcular a estatística de teste e compará-la com o valor crítico para rejeitar ou não a hipótese nula.

Deve-se notar que os testes de hipóteses têm nomes diferentes; em estatística, eles também são chamados de contrastes de hipóteses, testes de hipóteses ou testes de significância.

Fórmula de teste de hipóteses para média

A seguir veremos como a estatística do teste de hipótese para a média é calculada. No entanto, a fórmula varia ligeiramente dependendo se a variância é conhecida ou não, então veremos primeiro como isso é feito quando a variância é conhecida e depois quando a variância é desconhecida.

Com desvio conhecido

A fórmula da hipótese de teste para a média com variância conhecida é:

$\displaystyle Z=\frac{\overline{x}-\mu}{\displaystyle \frac{\sigma}{\sqrt{n}}}$

Ouro:

$Z$

é a estatística do teste de hipótese para a média.
$\overline{x}$

é a média amostral.
$\mu$

é o valor médio proposto.
$\sigma$

é o desvio padrão da população.
$n$

é o tamanho da amostra.

Uma vez calculada a estatística do teste de hipótese para a média, o resultado deve ser interpretado para rejeitar ou rejeitar a hipótese nula:

Se o teste de hipótese para a média for bilateral, a hipótese nula é rejeitada se o valor absoluto da estatística for maior que o valor crítico Z _α/2 .
Se o teste de hipótese para a média corresponder à cauda direita, a hipótese nula será rejeitada se a estatística for maior que o valor crítico Z _α .
Se o teste de hipótese para a média corresponder à cauda esquerda, a hipótese nula será rejeitada se a estatística for menor que o valor crítico -Z _α .

$\begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |Z|>Z_{\alpha/2} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z>Z_{\alpha} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z<-Z_{\alpha} \text{ se rechaza } H_0\end{array}$

Neste caso, os valores críticos são obtidos da tabela de distribuição normal padronizada .

Com variação desconhecida

A fórmula da hipótese de teste para a média com variância desconhecida é:

$\displaystyle t=\frac{\overline{x}-\mu}{\displaystyle \frac{s}{\sqrt{n}}}$

Ouro:

$t$

é a estatística de teste de hipótese para a média, que é definida por uma distribuição t de Student .
$\overline{x}$

é a média amostral.
$\mu$

é o valor médio proposto.
$s$

é o desvio padrão da amostra.
$n$

é o tamanho da amostra.

Como antes, o resultado calculado da estatística de teste deve ser interpretado com o valor crítico para rejeitar ou não a hipótese nula:

Se o teste de hipótese para a média for bilateral, a hipótese nula é rejeitada se o valor absoluto da estatística for maior que o valor crítico t _α/2|n-1 .
Se o teste de hipótese para a média corresponder à cauda direita, a hipótese nula será rejeitada se a estatística for maior que o valor crítico t _α|n-1 .
Se o teste de hipótese para a média corresponder à cauda esquerda, a hipótese nula será rejeitada se a estatística for menor que o valor crítico -t _α|n-1 .

$\begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |t|>t_{\alpha/2|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t>t_{\alpha|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t<-t_{\alpha|n-1} \text{ se rechaza } H_0\end{array}$

Quando a variância é desconhecida, os valores críticos do teste são obtidos na tabela de distribuição de Student.

Exemplo do mundo real de teste de hipóteses para a média

Para entender completamente o conceito de teste de hipótese para a média populacional, você pode ver abaixo um exemplo real desse tipo de teste de hipótese.

Uma empresa de tecnologia afirma que a bateria do laptop que vende dura 6 horas. Verificamos se esta hipótese é falsa realizando um teste de hipótese com nível de significância α = 0,05. Para isso, decide-se adquirir 20 unidades e observar a duração da bateria de cada computador (os valores são expressos em horas):

5,2 5,9 7,1 4,2 6,5
8,5 4,6 6,8 6,9 5,8
5,1 6,5 7,0 5,3 6,2
5,7 6,6 7,5 5,1 6,1

Neste caso, as hipóteses nula e alternativa do teste de hipótese sobre a média são as seguintes:

$\begin{cases}H_0: \mu=6\\[2ex] H_1:\mu\neq 6 \end{cases}$

Para determinar a estatística de teste, primeiro precisamos calcular a média amostral e o desvio padrão amostral:

$\overline{x}=6,13 \qquad s=1,05$

Como não conhecemos a variância populacional, para obter a estatística do teste precisamos aplicar a fórmula de teste de hipótese para a média com variância desconhecida:

$\displaystyle t=\frac{\overline{x}-\mu}{\displaystyle \frac{s}{\sqrt{n}}}$

$\displaystyle t=\frac{6,13-6}{\displaystyle \frac{1,05}{\sqrt{20}}}$

$\displaystyle t=0,68$

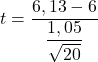
Agora precisamos encontrar o valor crítico do teste de hipótese, então procuramos na tabela de distribuição t de Student o valor correspondente. Os graus de liberdade do t de Student são um a menos que o tamanho da amostra (20-1=19) e, por outro lado, a probabilidade correspondente é metade do nível de significância (0,05/2= 0,025), uma vez que se trata de uma probabilidade bilateral. testando hipóteses.

$\alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}t_{\alpha/2| n-1}= \ \color{orange}\bm{?}\\[4ex]t_{0,025| 19}=2,093\end{array}$

Concluindo, por se tratar de um teste de hipótese bilateral e o valor absoluto da estatística de teste ser menor que o valor crítico, a hipótese nula não é rejeitada, mas a hipótese alternativa é rejeitada.

$0,68<2,093 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Se rechaza } H_1$

Teste de hipóteses para diferença de médias

O teste de hipótese de diferença de médias é usado para rejeitar ou aceitar a hipótese nula de que as médias de duas populações são iguais.

Assim, a hipótese nula de um teste de hipótese para a diferença de duas médias é sempre a seguinte:

$H_0: \mu_1=\mu_2$

Embora a hipótese alternativa possa ser uma das três seguintes:

$\begin{array}{l}H_1:\mu_1\neq \mu_2\\[2ex]H_1:\mu_1>\mu_2\\[2ex]H_1:\mu_1<\mu_2\end{array}$

Então, a fórmula para calcular a estatística do teste de hipótese para a diferença de médias quando a variância é conhecida é:

$\displaystyle Z=\frac{\displaystyle \overline{x_1}-\overline{x_2}}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}$

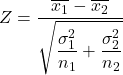
Ouro:

$Z$

é a estatística de teste de hipótese para a diferença de duas médias com variância conhecida, que segue uma distribuição normal padrão.
$\overline{x_1}$

é a média da amostra 1.
$\overline{x_2}$

é a média da amostra 2.
$\sigma_1^2$

é a variância da população 1.
$\sigma_2^2$

é a variância da população 2.
$n_1$

é o tamanho da amostra 1.
$n_2$

é o tamanho da amostra 2.

Por outro lado, a fórmula para calcular a estatística do teste de hipótese para a diferença de médias quando a variância é desconhecida é a seguinte:

$\displaystyle t=\frac{\displaystyle \overline{x_1}-\overline{x_2}}{\displaystyle\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$

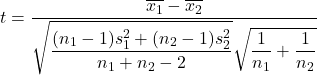
Ouro:

$t$

é a estatística de teste de hipótese para a diferença de duas médias com variância desconhecida, que segue a distribuição t de Student.
$\overline{x_1}$

é a média da amostra 1.
$\overline{x_2}$

é a média da amostra 2.
$s_1^2$

é a variância da amostra 1.
$s_2^2$

é a variância da amostra 2.
$n_1$

é o tamanho da amostra 1.
$n_2$

é o tamanho da amostra 2.

About Author

Dr. benjamim anderson

Olá, sou Benjamin, um professor aposentado de estatística que se tornou professor dedicado na Statorials. Com vasta experiência e conhecimento na área de estatística, estou empenhado em compartilhar meu conhecimento para capacitar os alunos por meio de Statorials. Saber mais

O que é teste de hipótese para a média?

Fórmula de teste de hipóteses para média

Com desvio conhecido

Com variação desconhecida

Exemplo do mundo real de teste de hipóteses para a média

Teste de hipóteses para diferença de médias

About Author

Dr. benjamim anderson

Add a Comment