Como testar a normalidade em python (4 métodos)

Muitos testes estatísticos assumem que os conjuntos de dados são normalmente distribuídos.

Existem quatro maneiras comuns de verificar essa hipótese em Python:

1. (Método visual) Crie um histograma.

• Se o histograma tiver aproximadamente o formato de um “sino”, então os dados serão considerados normalmente distribuídos.

2. (Método visual) Crie um gráfico QQ.

• Se os pontos no gráfico estiverem aproximadamente ao longo de uma linha reta diagonal, então os dados são considerados normalmente distribuídos.

3. (Teste estatístico formal) Realize um teste de Shapiro-Wilk.

• Se o valor p do teste for maior que α = 0,05, então os dados são considerados normalmente distribuídos.

4. (Teste estatístico formal) Realize um teste de Kolmogorov-Smirnov.

• Se o valor p do teste for maior que α = 0,05, então os dados são considerados normalmente distribuídos.

Os exemplos a seguir mostram como usar cada um desses métodos na prática.

Método 1: crie um histograma

O código a seguir mostra como criar um histograma para um conjunto de dados que segue uma distribuição log-normal :

 import math
import numpy as np
from scipy. stats import lognorm
import matplotlib. pyplot as plt

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#create histogram to visualize values in dataset
plt. hist (lognorm_dataset, edgecolor=' black ', bins=20) 

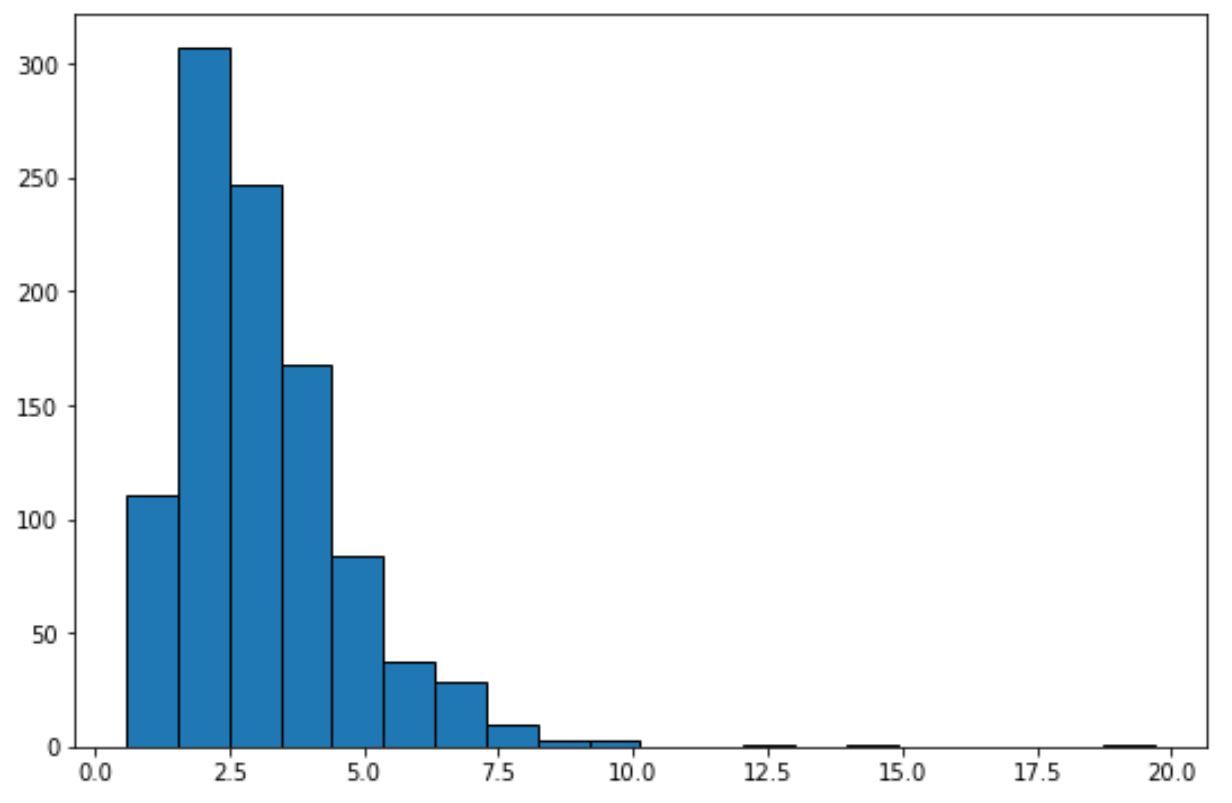
Apenas olhando para este histograma, podemos dizer que o conjunto de dados não apresenta um “formato de sino” e não é normalmente distribuído.

Método 2: criar um gráfico QQ

O código a seguir mostra como criar um gráfico QQ para um conjunto de dados que segue uma distribuição log-normal:

 import math
import numpy as np
from scipy. stats import lognorm
import statsmodels. api as sm
import matplotlib. pyplot as plt

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#create QQ plot with 45-degree line added to plot
fig = sm. qqplot (lognorm_dataset, line=' 45 ')

plt. show ()

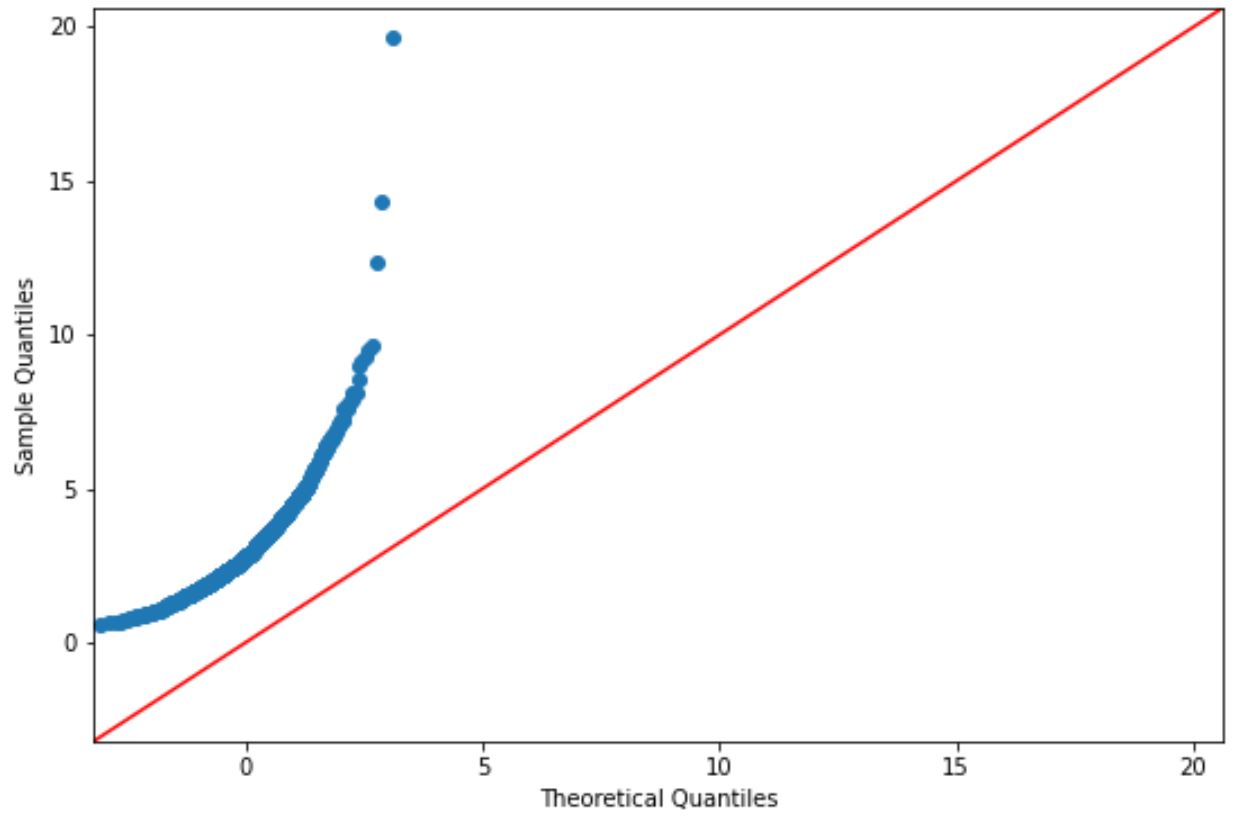
Se os pontos do gráfico estiverem aproximadamente ao longo de uma linha reta diagonal, geralmente assumimos que um conjunto de dados é normalmente distribuído.

No entanto, os pontos neste gráfico claramente não correspondem à linha vermelha, pelo que não podemos assumir que este conjunto de dados seja normalmente distribuído.

Isso deve fazer sentido, visto que geramos os dados usando uma função de distribuição log-normal.

Método 3: realizar um teste de Shapiro-Wilk

O código a seguir mostra como executar um Shapiro-Wilk para um conjunto de dados que segue uma distribuição log-normal:

 import math
import numpy as np
from scipy.stats import shapiro 
from scipy. stats import lognorm

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#perform Shapiro-Wilk test for normality
shapiro(lognorm_dataset)

ShapiroResult(statistic=0.8573324680328369, pvalue=3.880663073872444e-29)

A partir do resultado, podemos ver que a estatística de teste é 0,857 e o valor p correspondente é 3,88e-29 (extremamente próximo de zero).

Como o valor p é inferior a 0,05, rejeitamos a hipótese nula do teste de Shapiro-Wilk.

Isto significa que temos evidências suficientes para dizer que os dados da amostra não provêm de uma distribuição normal.

Método 4: realizar um teste de Kolmogorov-Smirnov

O código a seguir mostra como realizar um teste de Kolmogorov-Smirnov para um conjunto de dados que segue uma distribuição log-normal:

 import math
import numpy as np
from scipy.stats import kstest
from scipy. stats import lognorm

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#perform Kolmogorov-Smirnov test for normality
kstest(lognorm_dataset, ' norm ')

KstestResult(statistic=0.84125708308077, pvalue=0.0)

A partir do resultado, podemos ver que a estatística de teste é 0,841 e o valor p correspondente é 0,0 .

Como o valor p é inferior a 0,05, rejeitamos a hipótese nula do teste Kolmogorov-Smirnov.

Isto significa que temos evidências suficientes para dizer que os dados da amostra não provêm de uma distribuição normal.

Como lidar com dados não normais

Se um determinado conjunto de dados não for normalmente distribuído, muitas vezes podemos realizar uma das seguintes transformações para torná-lo mais normalmente distribuído:

1. Transformação de log: transforme valores de x em log(x) .

2. Transformação de raiz quadrada: Transforme os valores de x em √x .

3. Transformação da raiz cúbica: transforme os valores de x em x ^1/3 .

Ao realizar essas transformações, o conjunto de dados geralmente se torna distribuído de forma mais normal.

Leia este tutorial para ver como realizar essas transformações em Python.