Como testar a significância de uma inclinação de regressão

Digamos que temos o seguinte conjunto de dados que mostra a metragem quadrada e o preço de 12 casas diferentes:

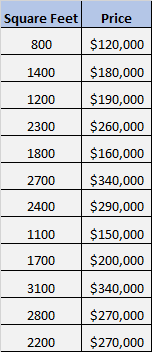
Queremos saber se existe uma relação significativa entre metragem quadrada e preço.

Para ter uma ideia da aparência dos dados, primeiro criamos um gráfico de dispersão com pés quadrados no eixo x e preço no eixo y:

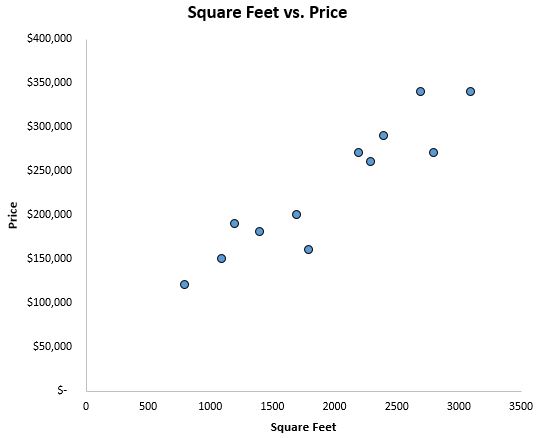
Podemos ver claramente que existe uma correlação positiva entre metragem quadrada e preço. À medida que a metragem quadrada aumenta, o preço da casa também tende a aumentar.

No entanto, para descobrir se existe uma relação estatisticamente significativa entre a metragem quadrada e o preço, precisamos executar uma regressão linear simples.

Portanto, executamos uma regressão linear simples usando pés quadrados como preditor e preço como resposta e obtemos o seguinte resultado:

Quer você execute uma regressão linear simples no Excel, SPSS, R ou qualquer outro software, obterá um resultado semelhante ao mostrado acima.

Lembre-se de que uma regressão linear simples produzirá a reta de melhor ajuste, que é a equação da reta que melhor “se ajusta” aos dados em nosso gráfico de dispersão. Esta linha de melhor ajuste é definida como:

ŷ = b ₀ + b ₁ x

onde ŷ é o valor previsto da variável de resposta, b ₀ é o intercepto, b ₁ é o coeficiente de regressão e x é o valor da variável preditora.

O valor de b ₀ é dado pelo coeficiente de origem, que é 47588,70.

O valor de b ₁ é dado pelo coeficiente da variável preditora Square Feet , que é 93,57.

Portanto, a linha de melhor ajuste neste exemplo é ŷ = 47588,70+ 93,57x

Veja como interpretar esta linha de melhor ajuste:

• b ₀ : Quando o valor dos pés quadrados é zero, o valor do preço médio esperado é de $ 47.588,70. (Neste caso não faz muito sentido interpretar a interceptação, já que uma casa nunca pode ter zero metro quadrado)
• b ₁ : Para cada metro quadrado adicional, o aumento médio esperado no preço é de US$ 93,57.

Portanto, sabemos agora que para cada metro quadrado adicional, o aumento médio esperado no preço é de US$ 93,57.

Para saber se este aumento é estatisticamente significativo, precisamos realizar um teste de hipótese para B ₁ ou construir um intervalo de confiança para B ₁ .

Nota : Um teste de hipótese e um intervalo de confiança sempre darão os mesmos resultados.

Construção de um intervalo de confiança para uma inclinação de regressão

Para construir um intervalo de confiança para uma inclinação de regressão, usamos a seguinte fórmula:

Intervalo de confiança = b ₁ +/- (t _{1-∝/2, n-2} ) * (erro padrão de b ₁ )

Ouro:

• b ₁ é o coeficiente de inclinação dado no resultado da regressão
• (t _{1-∝/2, n-2} ) é o valor t crítico para o nível de confiança 1-∝ com n-2 graus de liberdade, onde n é o número total de observações em nosso conjunto de dados
• (erro padrão de b ₁ ) é o erro padrão de b ₁ dado no resultado da regressão

Para nosso exemplo, veja como construir um intervalo de confiança de 95% para B ₁ :

• b ₁ é 93,57 da saída da regressão.
• Como estamos usando um intervalo de confiança de 95%, ∝ = 0,05 e n-2 = 12-2 = 10, então t _{0,975, 10} é 2,228 de acordo com a tabela de distribuição t
• (o erro padrão de _b1 ) é 11,45 da saída da regressão

Assim, nosso intervalo de confiança de 95% para B ₁ é:

93,57 +/- (2,228) * (11,45) = (68,06, 119,08)

Isso significa que estamos 95% confiantes de que o verdadeiro aumento médio do preço para cada metro quadrado adicional está entre US$ 68,06 e US$ 119,08.

Observe que US$ 0 não está nesse intervalo, portanto, a relação entre a metragem quadrada e o preço é estatisticamente significativa no nível de confiança de 95%.

Executando um teste de hipótese para uma inclinação de regressão

Para realizar um teste de hipótese para uma inclinação de regressão, seguimos as cinco etapas padrão para qualquer teste de hipótese :

Passo 1. Estabeleça as hipóteses.

A hipótese nula (H0): B ₁ = 0

A hipótese alternativa: (Ha): B ₁ ≠ 0

Passo 2. Determine um nível de significância a ser usado.

Como construímos um intervalo de confiança de 95% no exemplo anterior, usaremos aqui a abordagem equivalente e optaremos por usar um nível de significância de 0,05.

Etapa 3. Encontre a estatística de teste e o valor p correspondente.

Neste caso, a estatística de teste é t = coeficiente de b ₁ / erro padrão de b ₁ com n-2 graus de liberdade. Podemos encontrar estes valores no resultado da regressão:

Assim, a estatística de teste t = 92,89 / 13,88 = 6,69.

Usando a calculadora de pontuação T para valor P com uma pontuação de 6,69 com 10 graus de liberdade e um teste bicaudal, o valor p = 0,000 .

Passo 4. Rejeite ou não rejeite a hipótese nula.

Como o valor p está abaixo do nosso nível de significância de 0,05, rejeitamos a hipótese nula.

Etapa 5. Interprete os resultados.

Uma vez que rejeitamos a hipótese nula, temos provas suficientes para dizer que o verdadeiro aumento médio no preço por cada metro quadrado adicional não é zero.