Como usar o teste de dunnett para comparações múltiplas

Uma ANOVA (Análise de Variância) é usada para determinar se existe ou não uma diferença estatisticamente significativa entre as médias de três ou mais grupos independentes.

Se o valor p da ANOVA estiver abaixo de um determinado nível de significância escolhido, podemos rejeitar a hipótese nula e concluir que temos evidências suficientes para dizer que pelo menos uma das médias do grupo é diferente das outras.

No entanto, isso não nos diz quais grupos são diferentes uns dos outros. Isto simplesmente nos diz que nem todas as médias dos grupos são iguais. Para saber exatamente quais grupos são diferentes entre si, precisamos realizar um teste post-hoc .

Se um dos grupos do estudo for considerado grupo controle , devemos utilizar o teste de Dunnett como teste post-hoc após a ANOVA.

Teste Dunnett: definição

Podemos usar as duas etapas a seguir para realizar o teste de Dunnett:

Etapa 1: Encontre o valor crítico de Dunnett.

Primeiro, precisamos encontrar o valor crítico de Dunnett. Isso é calculado da seguinte forma:

Valor crítico de Dunnett: t _d √ 2MS _w /n

Ouro:

• t _d : O valor encontrado na tabela de Dunnett para um determinado nível alfa, número de grupos e tamanhos de amostra de grupo.
• MS _w : Os quadrados médios de “dentro do grupo” na tabela de resultados da ANOVA
• n: Tamanho da amostra do grupo

Passo 2: Compare as diferenças entre as médias dos grupos com o valor crítico de Dunnett.

A seguir calculamos a diferença absoluta entre a média de cada grupo e a média do grupo controle. Se a diferença exceder o valor crítico de Dunnett, então esta diferença é considerada estatisticamente significativa.

O exemplo a seguir mostra como realizar o teste de Dunnett na prática.

Teste Dunnett: exemplo

Suponha que um professor queira saber se duas novas técnicas de estudo têm o potencial de melhorar as notas dos seus alunos nos testes. Para testar isso, ela divide aleatoriamente sua turma de 30 alunos nos três grupos a seguir:

• Grupo controle: 10 alunos
• Novo estudo técnico 1: 10 alunos
• Novo estudo técnico 2: 10 alunos

Depois de uma semana usando a técnica de estudo atribuída, cada aluno faz o mesmo exame. Os resultados são os seguintes:

• Pontuação média no exame do grupo de controle: 81,6
• Pontuação média do exame para a nova técnica de estudo grupo 1: 85,8
• Pontuação média no exame de grupo New Study Technique 2: 87,7
• Quadrados médios de “Dentro do Grupo” na tabela de resultados da ANOVA: 23,3

Com essas informações, podemos realizar o teste de Dunnett para determinar se uma das duas novas técnicas de estudo produz notas médias de exames significativamente diferentes das do grupo de controle.

Etapa 1: Encontre o valor crítico de Dunnett.

Usando α = 0,05, tamanho da amostra do grupo n = 10 e total do grupo = 3, a tabela de Dunnett nos diz para usar um valor de 2,57 no cálculo do valor crítico.

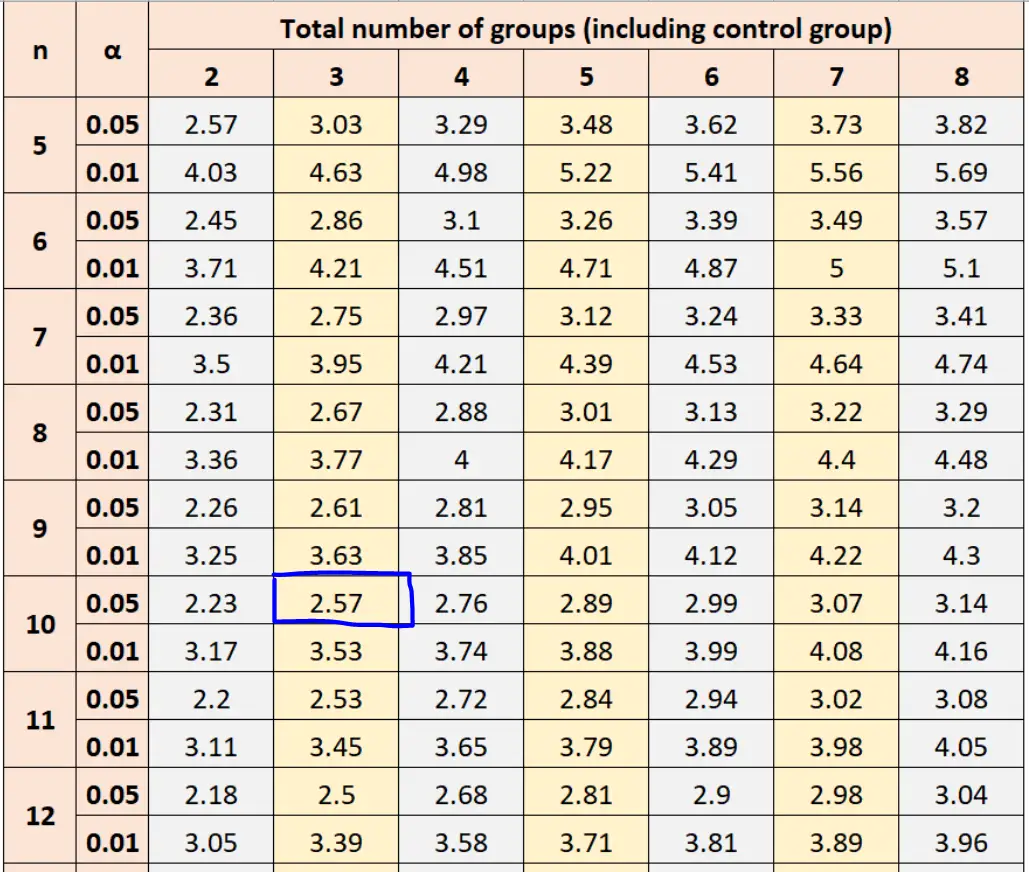
Então podemos inserir esse número na fórmula para encontrar o valor crítico de Dunnett:

Valor crítico de Dunnett: t _d √ 2MS _w /n = 2,57√ 2(23,3)/10 = 5,548

Passo 2: Compare as diferenças entre as médias dos grupos com o valor crítico de Dunnett.

As diferenças absolutas entre as médias de cada técnica de estudo e as do grupo controle são as seguintes:

• Abdômen. diferença entre a nova técnica 1 e o controle: |85,8 – 81,6| = 4,2
• Abdômen. diferença entre a nova técnica 2 e o controle: |87,7 – 81,6| = 6,1

Apenas a diferença absoluta entre a técnica 2 e o grupo controle é maior que o valor crítico de Dunnett de 5.548 .

Assim, podemos dizer que a nova técnica de estudo nº 2 produz resultados de exame significativamente diferentes em comparação ao grupo controle, mas este não é o caso da nova técnica de estudo nº 1.

Recursos adicionais

Uma introdução à ANOVA unidirecional
Um guia para usar testes post-hoc com ANOVA
Como realizar o teste de Dunnett em R