Como realizar o teste de white no sas

O teste de White é usado para determinar se a heterocedasticidade está presente em um modelo de regressão.

A heterocedasticidade refere-se à dispersão desigual de resíduos em diferentes níveis de uma variável de resposta em um modelo de regressão, o que viola uma das principais suposições da regressão linear de que os resíduos são igualmente dispersos em cada nível da variável de resposta.

Este tutorial explica como realizar o teste de White no SAS para determinar se a heterocedasticidade é ou não um problema em um determinado modelo de regressão.

Exemplo: teste branco em SAS

Suponha que queiramos ajustar um modelo de regressão linear múltipla que usa o número de horas gastas estudando e o número de exames práticos realizados para prever a nota do exame final dos alunos:

Nota do exame = β ₀ + β ₁ (horas) + β ₂ (exames preparatórios)

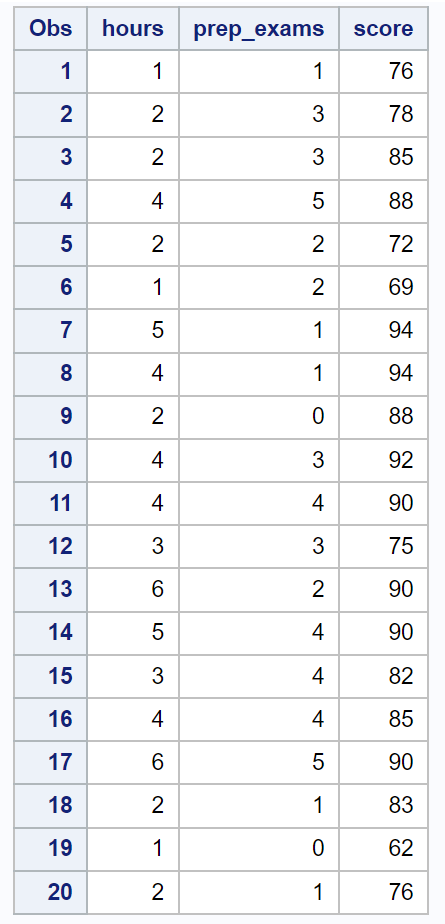
Primeiro, usaremos o seguinte código para criar um conjunto de dados contendo essas informações para 20 alunos:

 /*create dataset*/
data exam_data;
    input hours prep_exams score;
    datalines ;
1 1 76
2 3 78
2 3 85
4 5 88
2 2 72
1 2 69
5 1 94
4 1 94
2 0 88
4 3 92
4 4 90
3 3 75
6 2 90
5 4 90
3 4 82
4 4 85
6 5 90
2 1 83
1 0 62
2 1 76
;
run ;

/*view dataset*/
proc print data =exam_data; 

A seguir, usaremos proc reg para ajustar este modelo de regressão linear múltipla, bem como a opção spec para realizar o teste de White para heterocedasticidade:

 /*fit regression model and perform White's test*/
proc reg data =exam_data;
    model score = hours prep_exams / spec ;
run ;
quit ; 

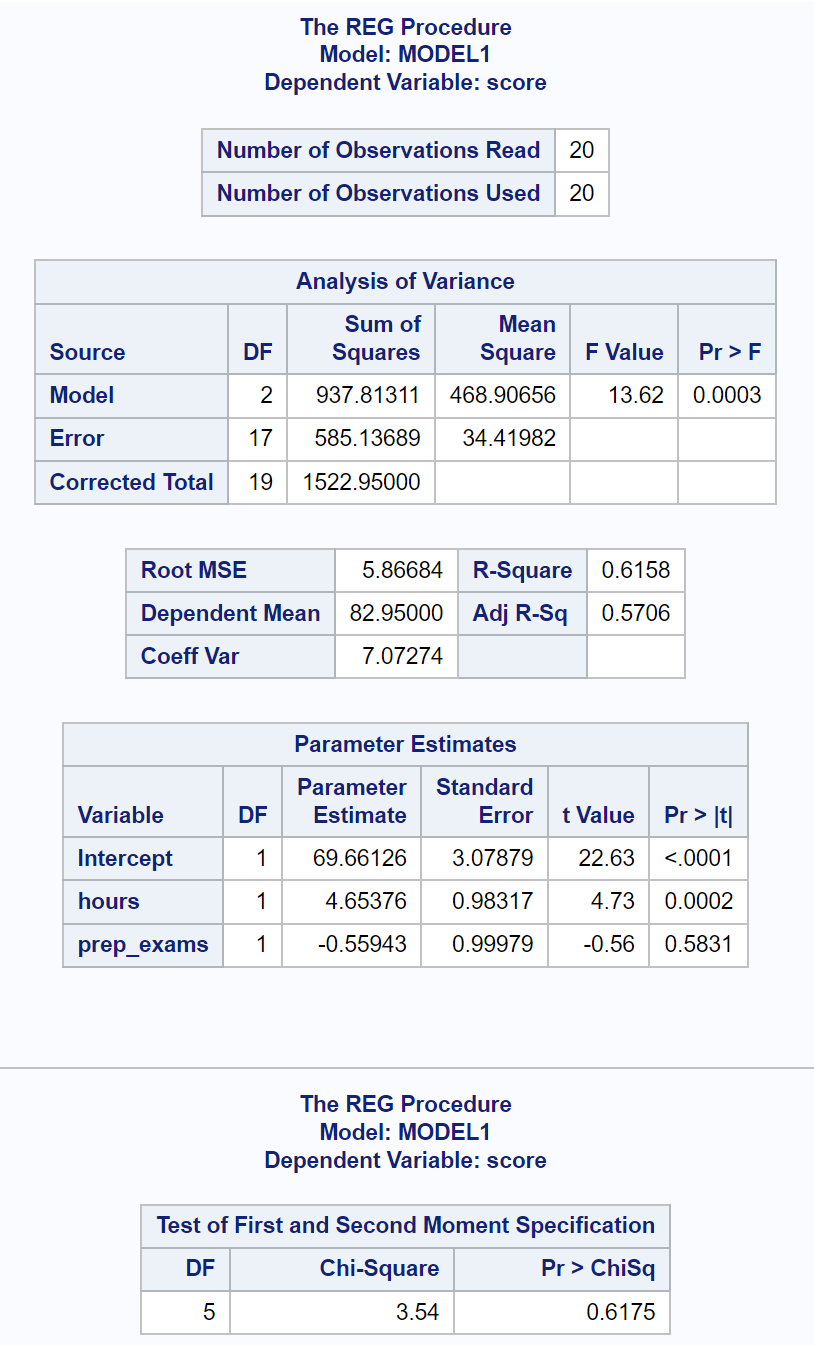
A última tabela de resultados mostra os resultados do teste de White.

Nesta tabela, podemos ver que a estatística do teste Qui-quadrado é 3,54 e o valor p correspondente é 0,6175 .

O teste de White utiliza as seguintes hipóteses nulas e alternativas:

• Nulo (H ₀ ) : A heterocedasticidade não está presente.
• Alternativa ( _HA ): A heterocedasticidade está presente.

Como o valor p não é inferior a 0,05, não rejeitamos a hipótese nula.

Isto significa que não temos evidências suficientes para afirmar que a heterocedasticidade está presente no modelo de regressão.

É portanto possível interpretar com segurança os erros padrão das estimativas dos coeficientes na tabela de resumo da regressão.

O que fazer a seguir

Se você não rejeitar a hipótese nula do teste de White, então a heterocedasticidade não estará presente e você poderá interpretar o resultado da regressão original.

Porém, se você rejeitar a hipótese nula, significa que a heterocedasticidade está presente nos dados. Neste caso, os erros padrão exibidos na tabela de resultados da regressão podem não ser confiáveis.

Existem várias maneiras comuns de resolver esse problema, incluindo:

1. Transforme a variável de resposta. Você pode tentar realizar uma transformação na variável de resposta.

Por exemplo, você pode usar a variável de resposta de log em vez da variável de resposta original.

Geralmente , obter o log da variável de resposta é uma forma eficaz de fazer desaparecer a heterocedasticidade.

Outra transformação comum é usar a raiz quadrada da variável de resposta.

2. Use regressão ponderada. Este tipo de regressão atribui um peso a cada ponto de dados com base na variância do seu valor ajustado.

Isso atribui pesos pequenos aos pontos de dados que possuem variâncias mais altas, reduzindo seus quadrados residuais.

Quando os pesos apropriados são usados, isso pode eliminar o problema da heterocedasticidade.