Como realizar um teste kruskal-wallis no excel

Um teste de Kruskal-Wallis é usado para determinar se existe ou não uma diferença estatisticamente significativa entre as medianas de três ou mais grupos independentes. É considerado o equivalente não paramétrico da ANOVA unidirecional.

Este tutorial explica como realizar um teste Kruskal-Wallis no Excel.

Exemplo: teste Kruskal-Wallis no Excel

Os pesquisadores querem saber se três fertilizantes diferentes levam a diferentes níveis de crescimento das plantas. Eles selecionam aleatoriamente 30 plantas diferentes e as dividem em três grupos de 10, aplicando um fertilizante diferente em cada grupo. Depois de um mês, medem a altura de cada planta.

Siga as etapas a seguir para realizar um teste de Kruskal-Wallis para determinar se o crescimento médio é o mesmo em todos os três grupos.

Passo 1: Insira os dados.

Insira os seguintes dados, que mostram o crescimento total (em polegadas) de cada uma das 10 plantas de cada grupo:

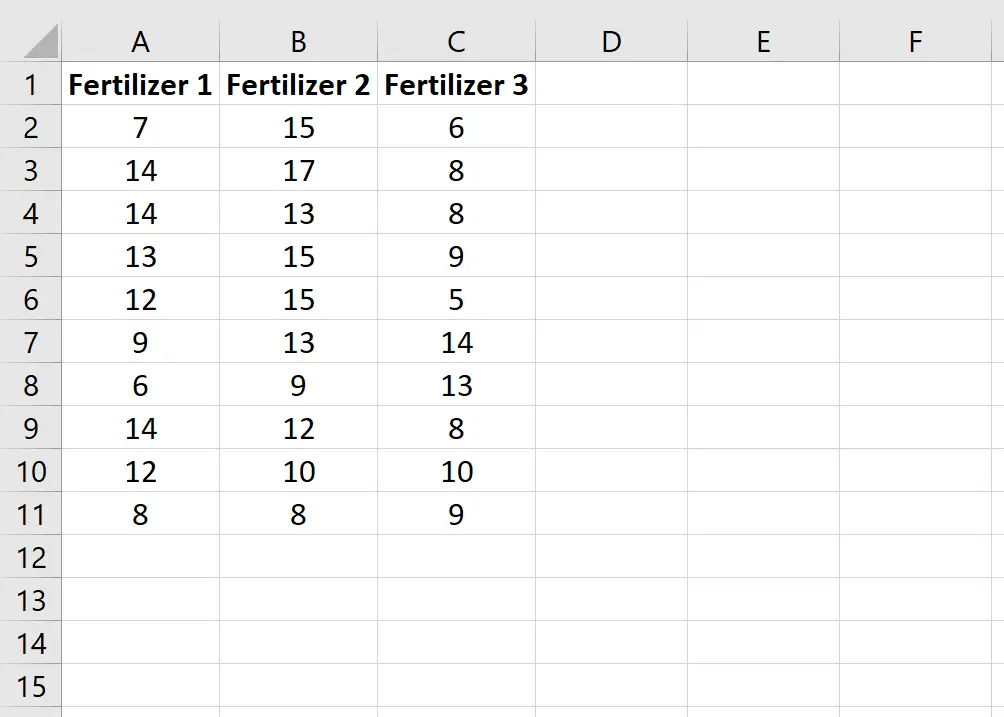
Etapa 2: Classifique os dados.

A seguir, usaremos a função RANK.AVG() para atribuir uma classificação ao crescimento de cada planta entre as 30 plantas. A fórmula a seguir mostra como calcular a classificação da primeira planta do primeiro grupo:

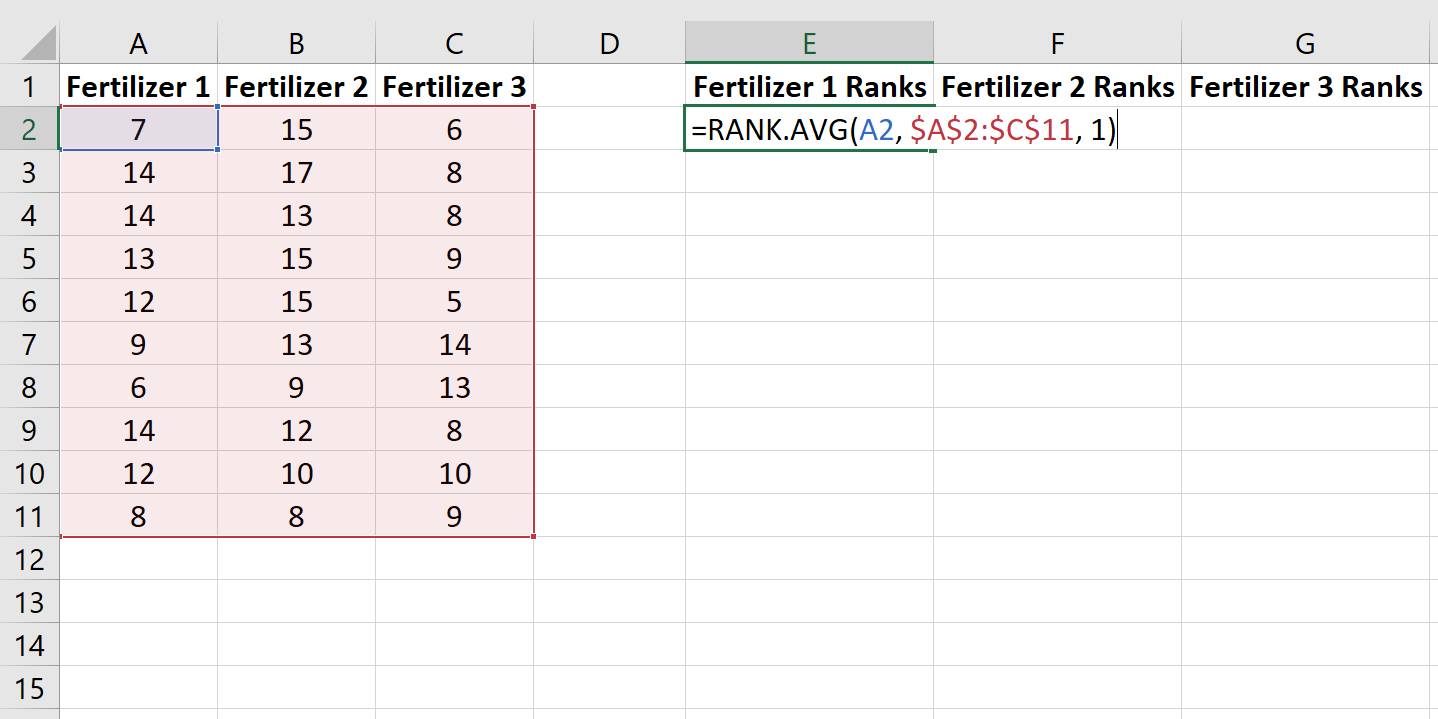
Copie esta fórmula para o restante das células:

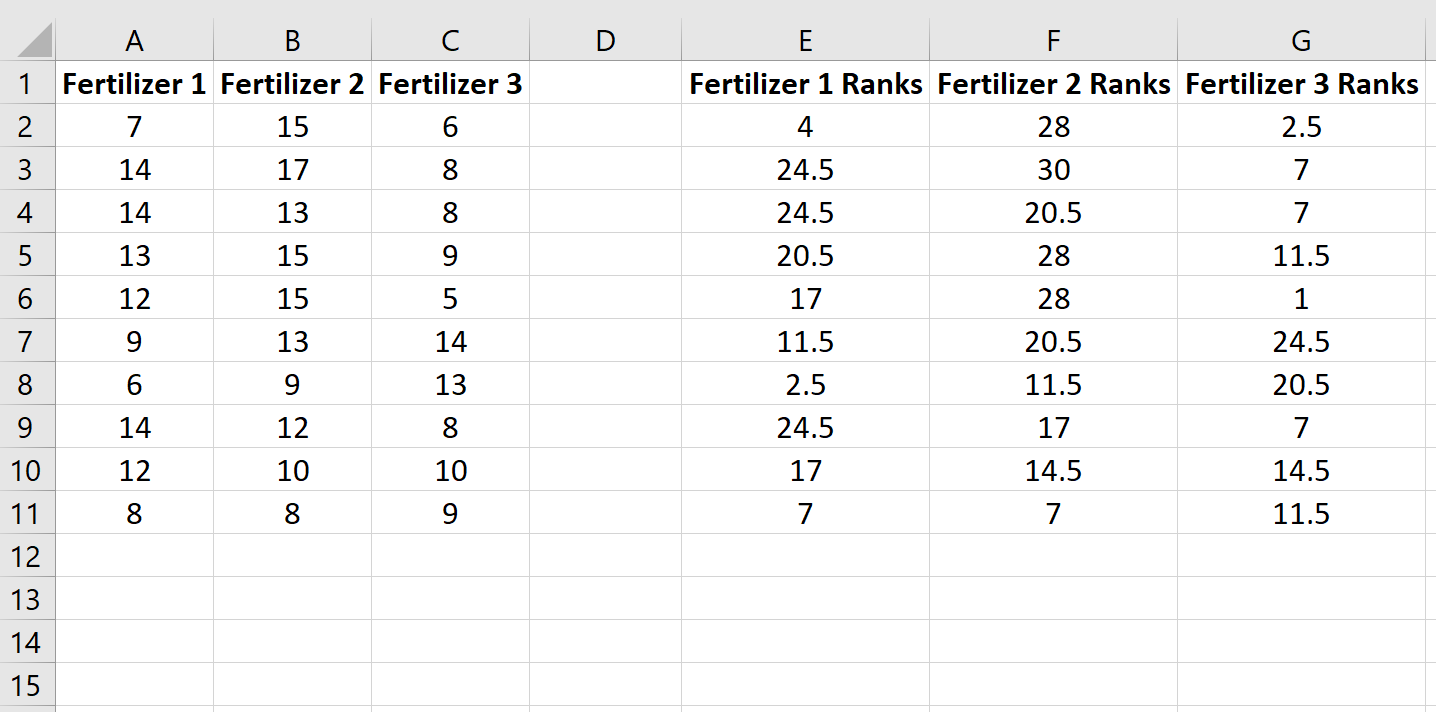
Em seguida, calcule a soma das classificações de cada coluna junto com o tamanho da amostra e a soma quadrada das classificações dividida pelo tamanho da amostra:

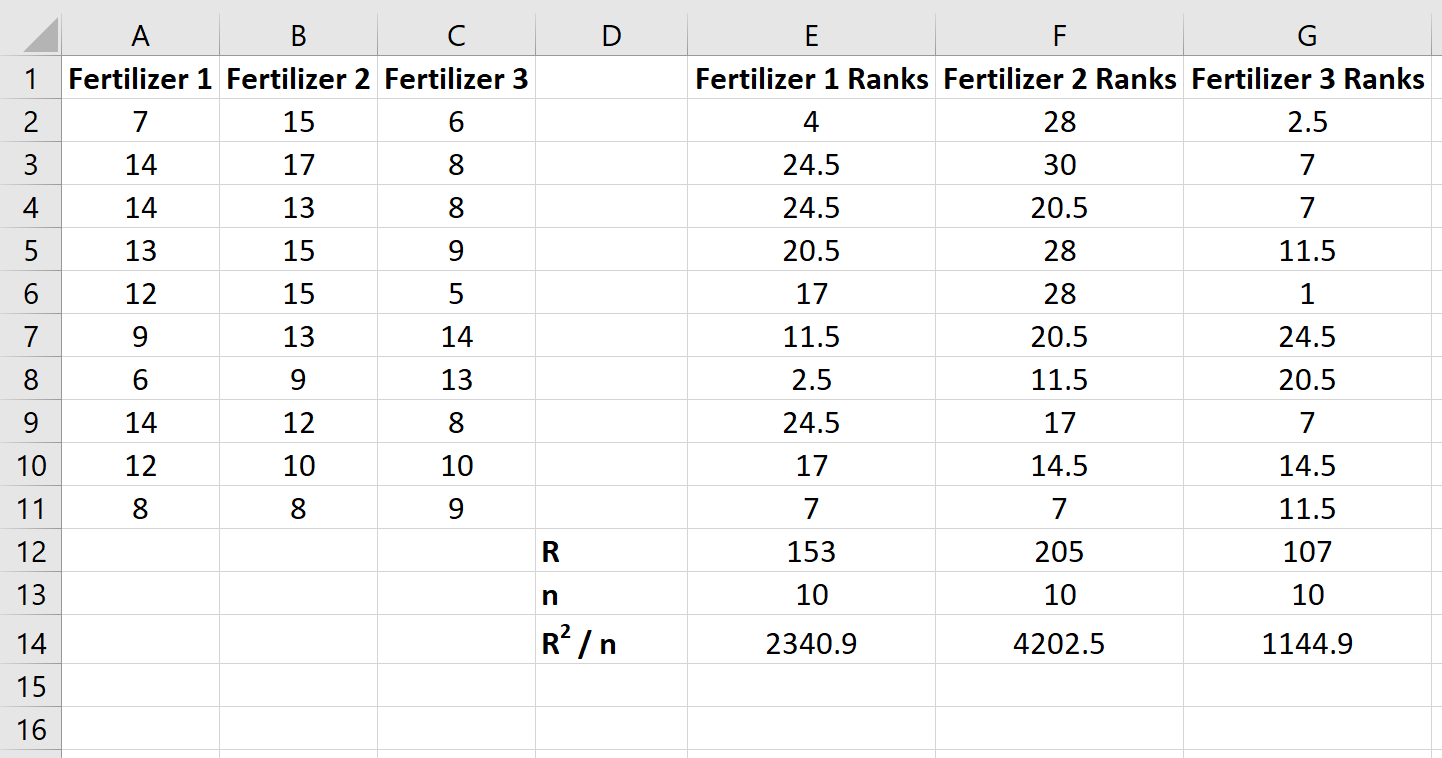
Etapa 3: Calcule a estatística de teste e o valor p correspondente.

A estatística de teste é definida como:

H = 12/(n(n+1)) * ΣR _j ² /n _j – 3(n+1)

Ouro:

• n = tamanho total da amostra
• R _j ² = soma das classificações do ^j-ésimo grupo
• n _j = tamanho da amostra do ^j-ésimo grupo

Sob a hipótese nula, H segue uma distribuição qui-quadrado com k-1 graus de liberdade.

A captura de tela a seguir mostra as fórmulas usadas para calcular a estatística de teste, H, e o valor p correspondente:

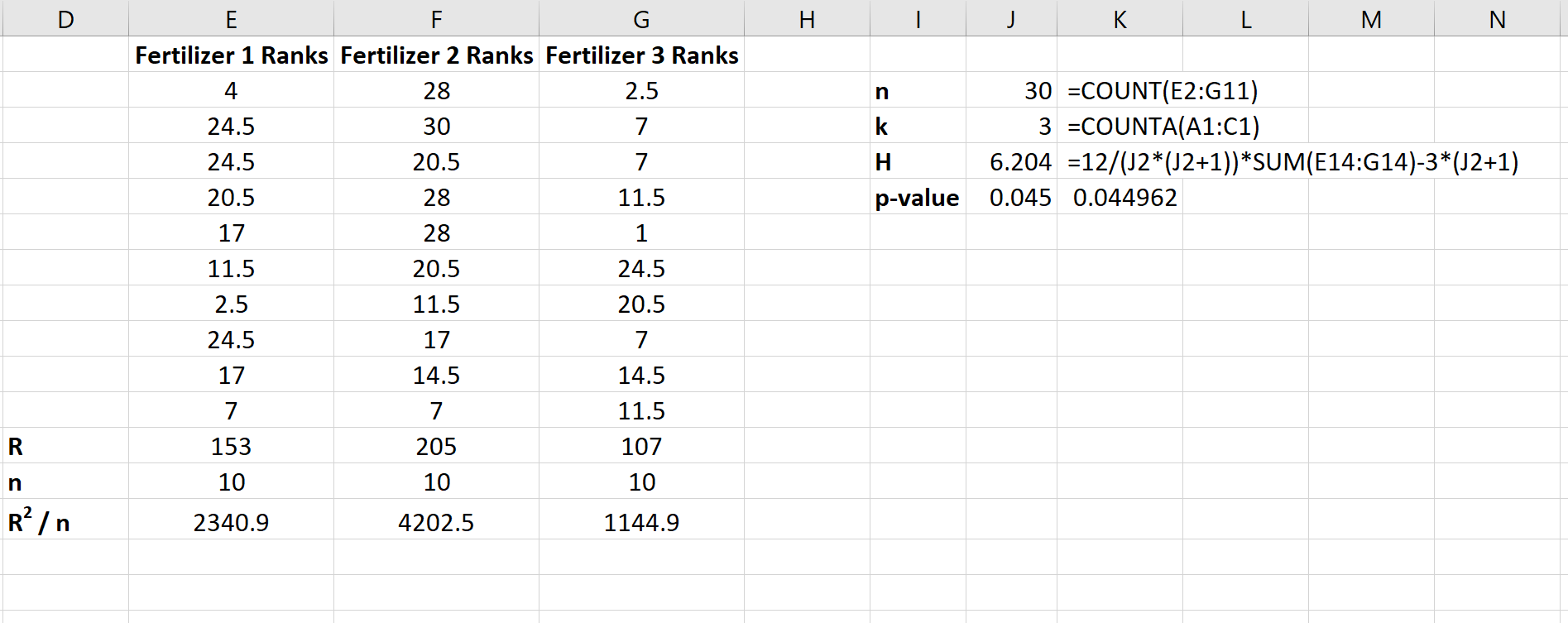
A estatística de teste é H = 6,204 e o valor p correspondente é p = 0,045 . Como este valor p é inferior a 0,05, podemos rejeitar a hipótese nula de que o crescimento médio das plantas é o mesmo para todos os três fertilizantes. Temos evidências suficientes para concluir que o tipo de fertilizante utilizado causa diferenças estatisticamente significativas no crescimento das plantas.

Etapa 4: relatar os resultados.

Por fim, gostaríamos de reportar os resultados do teste Kruskal-Wallis. Aqui está um exemplo de como fazer isso:

Um teste de Kruskal-Wallist foi realizado para determinar se o crescimento médio das plantas era o mesmo para três fertilizantes vegetais diferentes. Um total de 30 plantas foram utilizadas na análise. Cada fertilizante foi aplicado em 10 plantas diferentes.

O teste revelou que o crescimento médio das plantas não foi o mesmo (H = 6,204, p = 0,045) entre os três fertilizantes. Ou seja, houve uma diferença estatisticamente significativa no crescimento médio das plantas entre dois ou mais fertilizantes.