Como realizar um teste kruskal-wallis no spss

Um teste de Kruskal-Wallis é usado para determinar se existe ou não uma diferença estatisticamente significativa entre as medianas de três ou mais grupos independentes. É considerado o equivalente não paramétrico da ANOVA unidirecional .

Este tutorial explica como realizar um teste Kruskal-Wallis no SPSS.

Exemplo: teste Kruskal-Wallis no SPSS

Um pesquisador quer saber se três medicamentos têm efeitos diferentes na dor no joelho. Então, ele recruta 30 pessoas que sentem dores semelhantes nos joelhos e as divide aleatoriamente em três grupos para receber o medicamento 1, o medicamento 2 ou o medicamento 3.

Após um mês de uso do medicamento, o pesquisador pede a cada indivíduo que avalie sua dor no joelho em uma escala de 1 a 100, sendo 100 indicando a dor mais intensa. As pontuações das 30 pessoas são apresentadas abaixo:

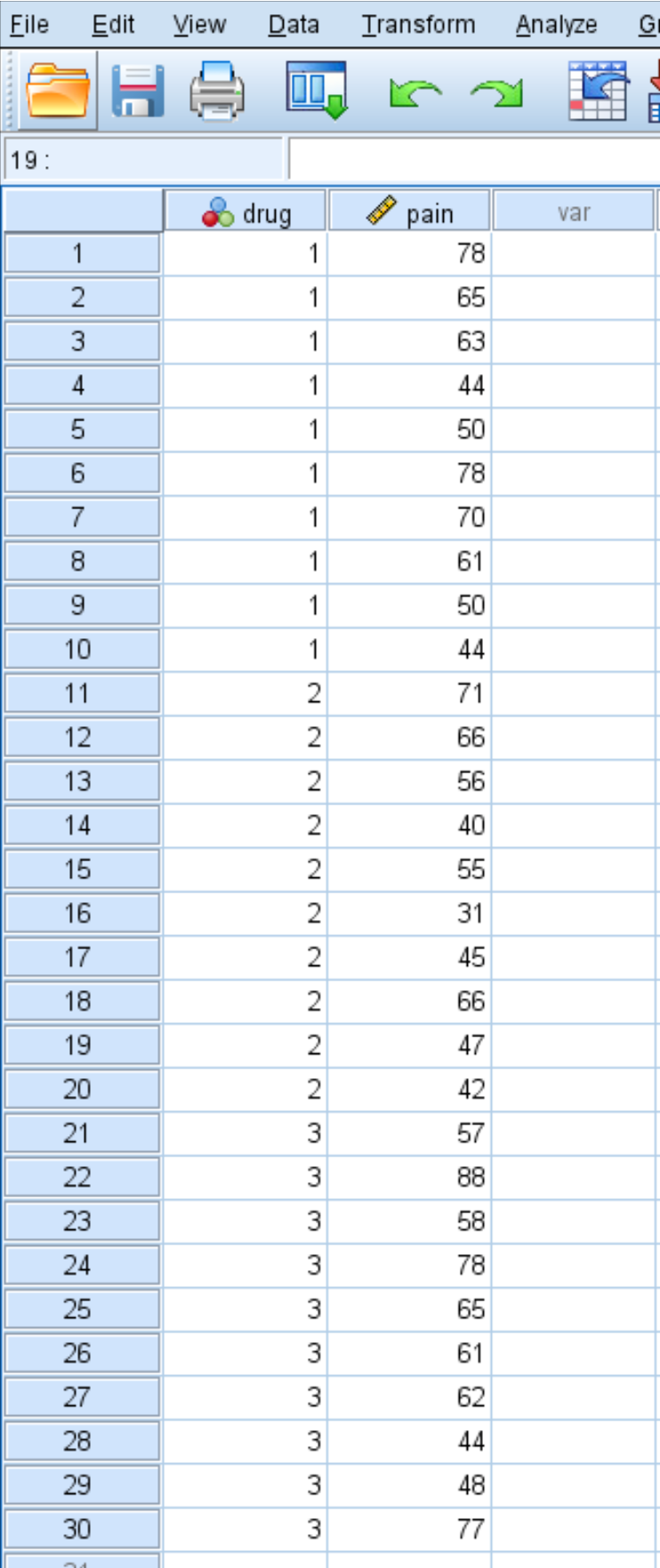
Siga as etapas a seguir para realizar um teste de Kruskal-Wallis para determinar se há ou não uma diferença nos níveis relatados de dor no joelho entre os três grupos:

Etapa 1: execute um teste de Kruskal-Wallis.

Clique na guia Analisar , depois em Testes Não Paramétricos , em Diálogos Legados e em K Amostras Independentes :

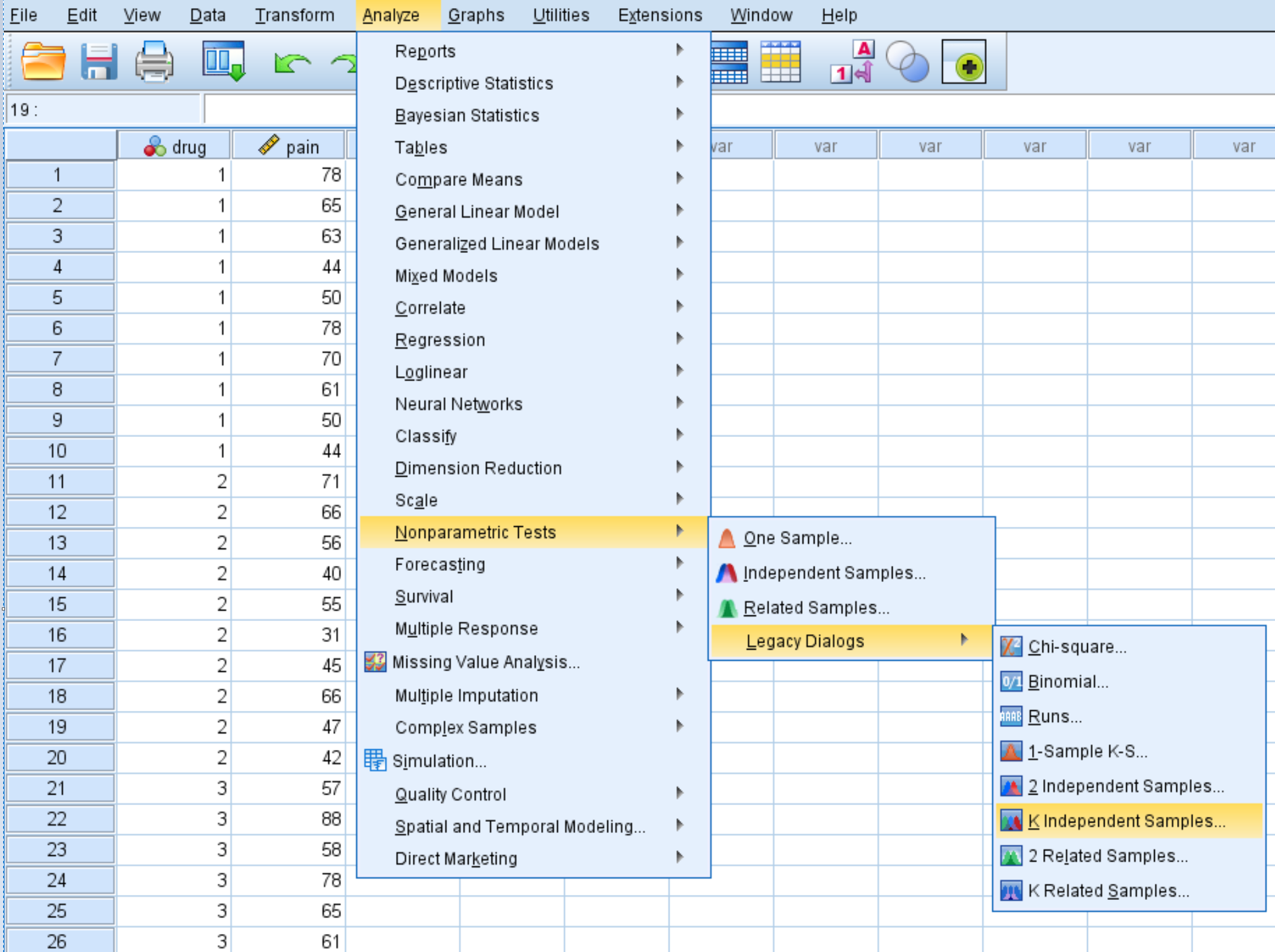
Na janela que aparece, arraste a variável dor para a caixa denominada Lista de variáveis de teste e medicamento para a caixa denominada Variável de agrupamento. Em seguida, clique em Definir intervalo e defina o valor mínimo como 1 e o valor máximo como 3. Em seguida, clique em Continuar . Certifique-se de que a caixa ao lado de Kruskal-Wallis H esteja marcada e clique em OK .

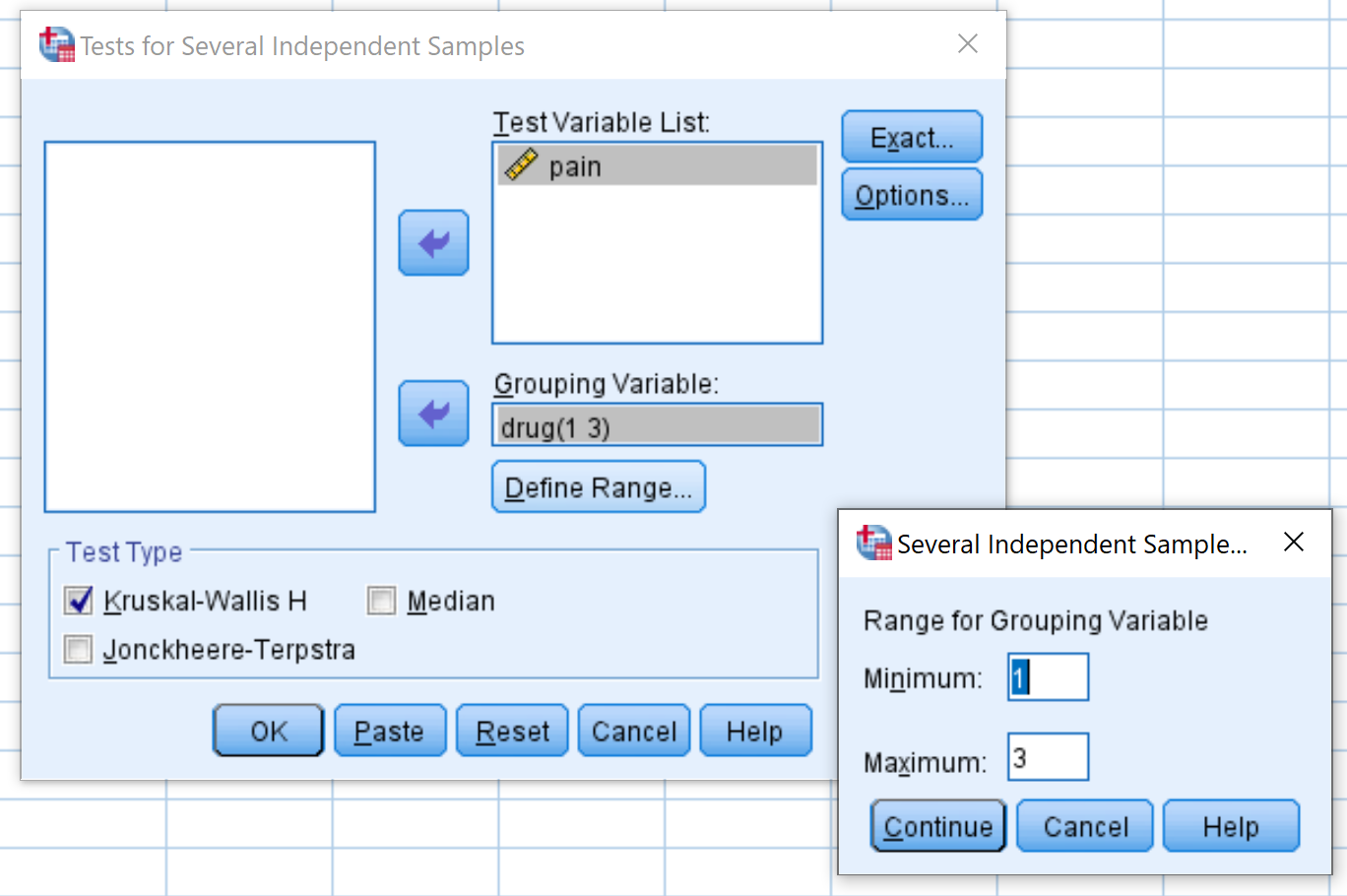
Etapa 2: interprete os resultados.

Depois de clicar em OK , os resultados do teste Kruskal-Wallis aparecerão:

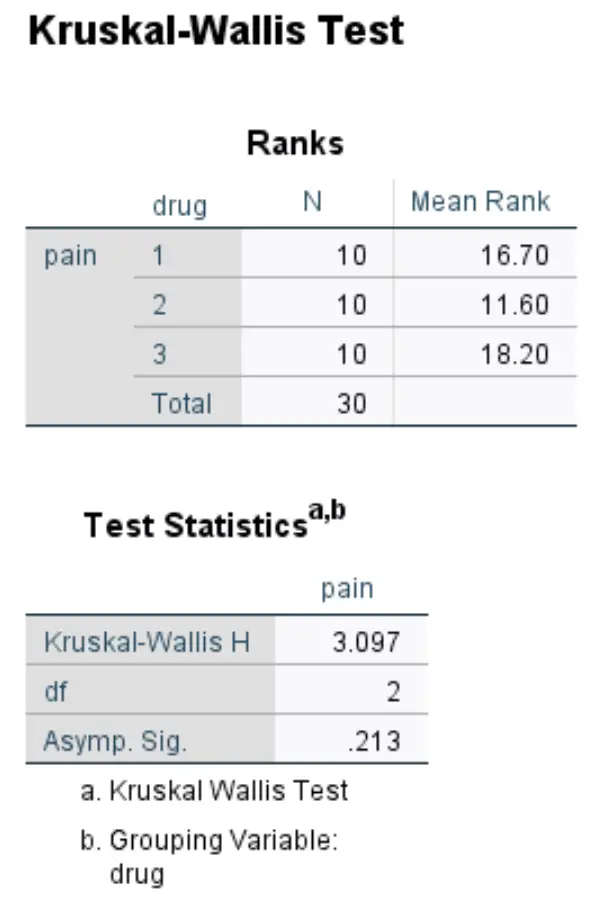
A segunda tabela na saída exibe os resultados do teste:

• Kruskal-Wallis H: Esta é a estatística do teste X ² .
• df: Estes são os graus de liberdade, calculados como #groups-1 = 3-1 = 2.
• Assímp. Sig: Este é o valor p associado a uma estatística de teste X ² de 3,097 com 2 graus de liberdade. Isso também pode ser encontrado usando a pontuação do qui-quadrado para a calculadora do valor P.

Como o valor p (0,213) não é inferior a 0,05, não rejeitamos a hipótese nula. Não temos evidências suficientes para afirmar que exista uma diferença estatisticamente significativa nas classificações de dor no joelho entre esses três grupos.