O que é um teste multinomial? (definição e #038; exemplo)

Um teste multinomial é usado para determinar se uma variável categórica segue uma distribuição hipotética.

Este teste usa as seguintes hipóteses nulas e alternativas:

H ₀ : Uma variável categórica segue uma distribuição hipotética.

_HA : Uma variável categórica não segue a distribuição hipotética.

Se o valor p do teste estiver abaixo de um determinado nível de significância (ex. α = 0,05), então podemos rejeitar a hipótese nula e concluir que a variável não segue a distribuição hipotética.

Este teste é usado quando uma variável pode levar k resultados diferentes. Um exemplo clássico de teste multinomial é quando queremos determinar se certos dados são justos. Quando você lança um dado, a probabilidade de ele cair em cada número (1 a 6) é 1/6.

Para testar se um dado é justo, podemos lançá-lo várias vezes e ver se o número de vezes que cai em números diferentes é significativamente diferente do que esperaríamos.

Os exemplos a seguir mostram como realizar um teste multinomial usando a linguagem de programação estatística R.

Exemplo 1: Dados Justos

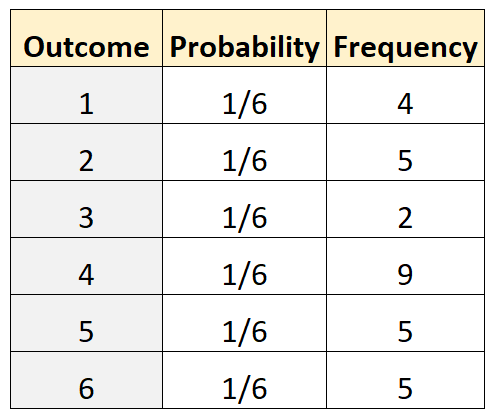
Suponha que queiramos determinar se um dado é justo. Para testar isso, executamos 30 vezes e registramos a frequência de cada resultado. A tabela a seguir mostra os resultados:

O seguinte código em R pode ser usado para realizar um teste multinomial:

 library (EMT)

#specify probability of each outcome
prob <- c(1/6, 1/6, 1/6, 1/6, 1/6, 1/6)

#specify frequency of each outcome from experiment
actual <- c(4, 5, 2, 9, 5, 5)

#perform multinomial test
multinomial. test (actual, prob) 

 Exact Multinomial Test, distance measure: p

    Events pObs p.value
    324632 0 0.4306

O valor p do teste é 0,4306 . Como este valor p não é inferior a 0,05, não rejeitaremos a hipótese nula. Portanto, não temos provas suficientes para dizer que os dados são injustos.

Exemplo 2: Vendas de produtos

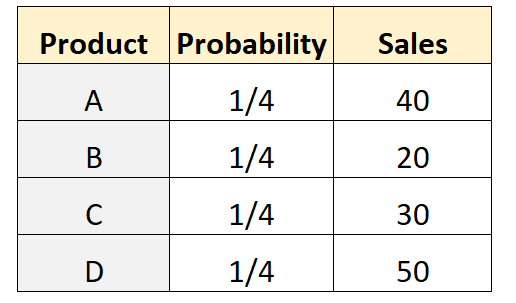
Suponha que o dono de uma loja suponha que um número igual de clientes comprará cada um dos quatro produtos diferentes. Para testar isso, ele registra o número de clientes que compraram cada produto em uma determinada semana. A tabela a seguir mostra os resultados:

O seguinte código em R pode ser usado para realizar um teste multinomial neste conjunto de dados:

 library (EMT)

#specify probability of each outcome
prob <- c(1/4, 1/4, 1/4, 1/4)

#specify frequency of each outcome from experiment
actual <- c(40, 20, 30, 50)

#perform multinomial test
multinomial. test (actual, prob) 

 Exact Multinomial Test, distance measure: p

    Events pObs p.value
    477191 0 0.00226

O valor p do teste é 0,00226 . Como este valor p é inferior a 0,05, rejeitaremos a hipótese nula. Portanto, temos evidências suficientes para afirmar que as vendas não são iguais para cada produto.

Exemplo 3: bolinhas de gude em um saco

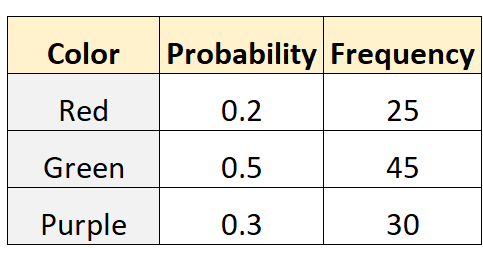
Tom afirma que a probabilidade de escolher uma bola de gude vermelha, verde ou roxa de um saco é de 0,2, 0,5 e 0,3, respectivamente. Para testar isso, seu amigo Mike enfia a mão no saco e tira uma bola de gude (com reposições) 100 vezes diferentes. A tabela a seguir mostra os resultados:

O seguinte código em R pode ser usado para realizar um teste multinomial neste conjunto de dados:

 library (EMT)

#specify probability of each outcome
prob <- c(.2, .5, .3)

#specify frequency of each outcome from experiment
actual <- c(40, 20, 30, 50)

#perform multinomial test
multinomial. test (actual, prob) 

 Exact Multinomial Test, distance measure: p

    Events pObs p.value
      5151 0.0037 0.3999

O valor p do teste é 0,3999 . Como esse valor p não é inferior a 0,05, não conseguiremos rejeitar a hipótese nula. Portanto, não temos evidências suficientes para afirmar que a distribuição das bolinhas de gude no saco seja diferente daquela especificada por Tom.

Recursos adicionais

Uma introdução à distribuição multinomial
Calculadora de distribuição multinomial