O que é o teste q de cochran? (definição e #038; exemplo)

O teste Q de Cochran é um teste estatístico usado para determinar se a proporção de “sucessos” é igual em três ou mais grupos em que os mesmos indivíduos aparecem em cada grupo.

Por exemplo, podemos usar o teste Q de Cochran para determinar se a proporção de alunos que passam em um teste é igual ao usar três técnicas de estudo diferentes.

Etapas para realizar o teste Q de Cochran

O teste Q de Cochran usa as seguintes hipóteses nulas e alternativas:

Hipótese nula (H ₀ ): A proporção de “sucessos” é a mesma em todos os grupos

Hipótese alternativa ( _HA ): A proporção de “sucessos” é diferente em pelo menos um dos grupos

A estatística de teste é calculada da seguinte forma:

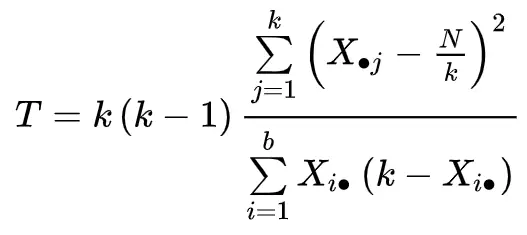
Ouro:

• k: O número de tratamentos (ou “grupos”)
• Xj: o total da coluna para o ^j-ésimo tratamento
• b: O número de blocos
• XI. : O total da linha para o ^i-ésimo bloco
• N: O total geral

A estatística do teste T segue uma distribuição qui-quadrado com k-1 graus de liberdade.

Se o valor p associado à estatística de teste estiver abaixo de um certo nível de significância (como α = 0,05), podemos rejeitar a hipótese nula e concluir que temos evidências suficientes para dizer que a proporção de “sucessos” é diferente em pelo menos um dos grupos.

Exemplo: teste Q de Cochran

Suponha que um pesquisador queira saber se três técnicas de estudo diferentes levam a proporções diferentes de taxas de sucesso entre os alunos.

Para testar isso, ela recruta 20 alunos, cada um fazendo um exame de igual dificuldade usando três técnicas de estudo diferentes. Os resultados são mostrados abaixo:

Para realizar o teste Q de Cochran, podemos usar software estatístico porque pode ser entediante realizá-lo manualmente.

Aqui está o código que podemos usar para criar este conjunto de dados e realizar o teste Q de Cochran na linguagem de programação estatística R:

 #load DescTools package
library (DescTools)

#create dataset
df <- data.frame(student= rep (1:20, each = 3 ),
                 technique= rep (c('A', 'B', 'C'), times= 20 ),
                 outcome=c(1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1,
                           1, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 1,
                           1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1,
                           1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1))

#perform Cochran's Q test
CochranQTest(outcome ~ technique| student, data=df)

	Cochran's Q test

data: outcome and technique and student
Q = 0.33333, df = 2, p-value = 0.8465

A partir do resultado do teste podemos observar o seguinte:

• A estatística de teste é 0,333
• O valor p correspondente é 0,8465

Como esse valor p não é inferior a 0,05, não rejeitamos a hipótese nula.

Isso significa que não temos evidências suficientes para afirmar que a técnica de estudo utilizada pelos alunos leva a diferentes proporções de taxas de sucesso.