Teste de independência qui-quadrado em uma calculadora ti-84
Um teste de independência do qui-quadrado é usado para determinar se existe ou não uma associação significativa entre duas variáveis categóricas.
Este tutorial explica como realizar um teste de independência qui-quadrado em uma calculadora TI-84.
Exemplo: teste de independência qui-quadrado em uma calculadora TI-84
Suponhamos que queremos saber se o género está ou não associado à preferência por um partido político. Pegamos uma amostra aleatória simples de 500 eleitores e perguntamos-lhes sobre suas preferências partidárias. A tabela a seguir apresenta os resultados da pesquisa:
| Republicano | Democrata | Independente | Total | |
| Macho | 120 | 90 | 40 | 250 |
| Fêmea | 110 | 95 | 45 | 250 |
| Total | 230 | 185 | 85 | 500 |
Utilize os passos seguintes para realizar um teste qui-quadrado de independência para determinar se o género está associado à preferência partidária política.
Passo 1: Insira os dados.
Primeiro, inseriremos os dados em uma matriz. Pressione 2 e depois pressione x -1 . Role para baixo até Editar , destaque qualquer matriz vazia e pressione Enter . A seguir, escolha o número de linhas (2 no nosso caso) e colunas (3 no nosso caso) para usar na matriz e insira os dados brutos:
Etapa 2: realize um teste de independência do qui-quadrado.
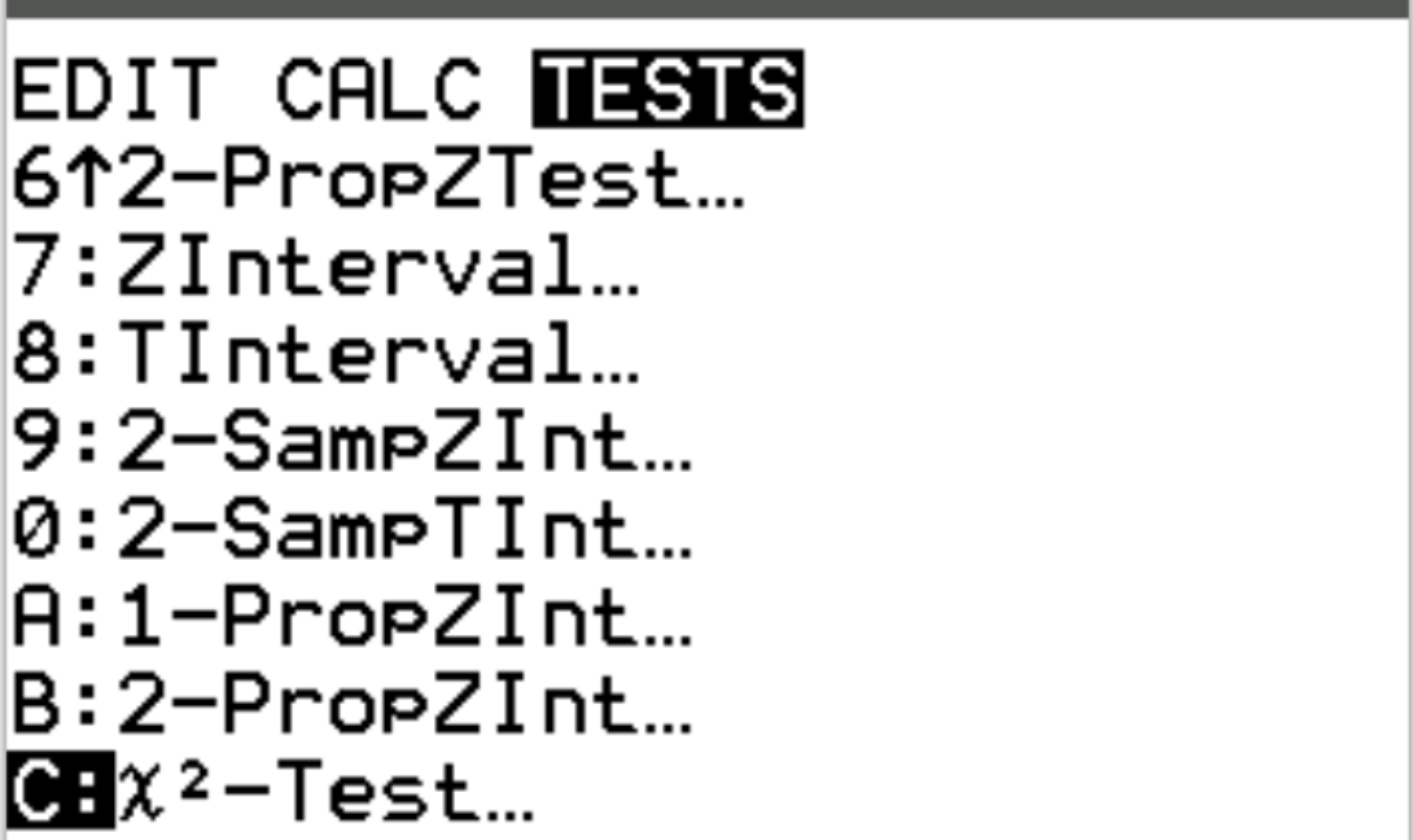
A seguir, realizaremos um teste de independência do qui-quadrado na matriz que acabamos de criar. Pressione stat e vá até TESTES . Em seguida, role para baixo até X 2 -Test e pressione Enter .
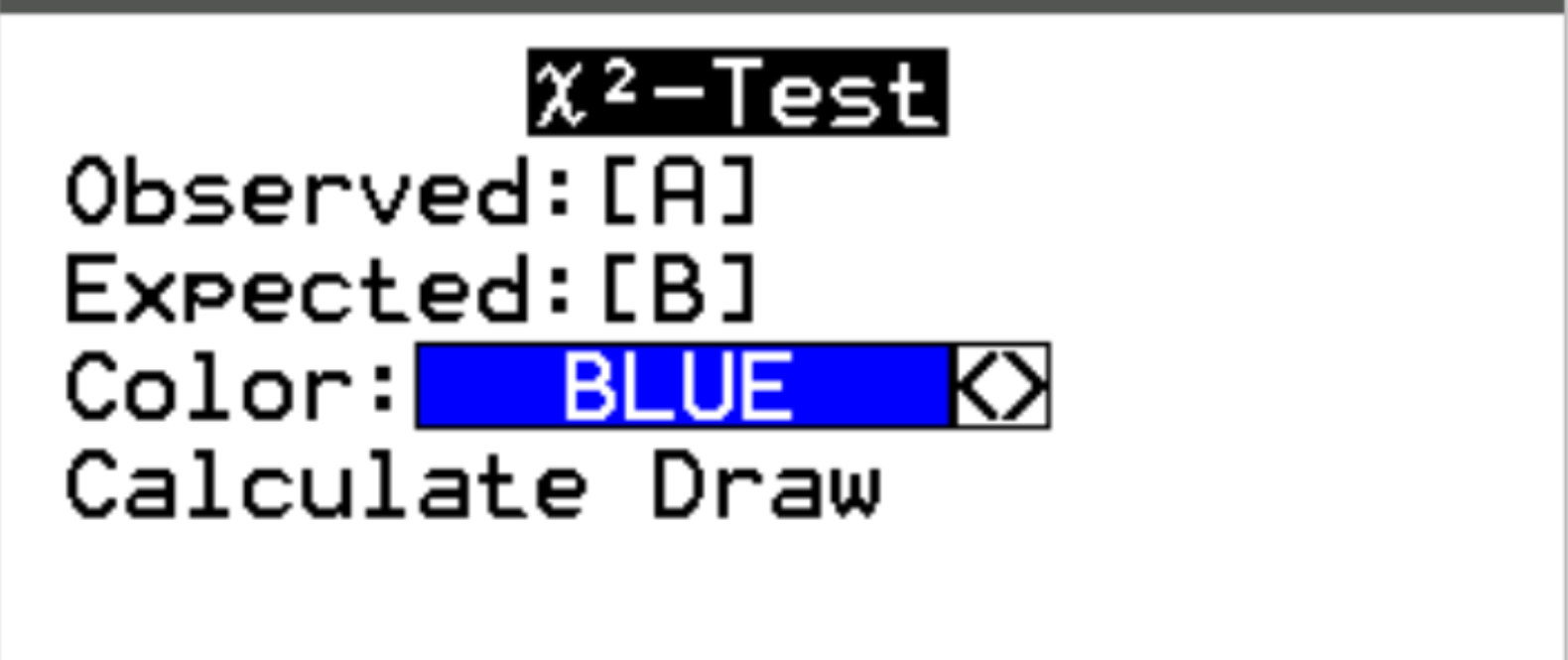
Para Observado , escolha a matriz na qual você inseriu os dados. No nosso caso, usamos a matriz A. Para Expected , pode ser qualquer matriz vazia (a calculadora produzirá automaticamente os valores esperados para nós). No nosso caso, deixaremos isso como matriz B.
Em seguida, destaque Calcular e pressione Enter .
A seguinte saída será exibida automaticamente:
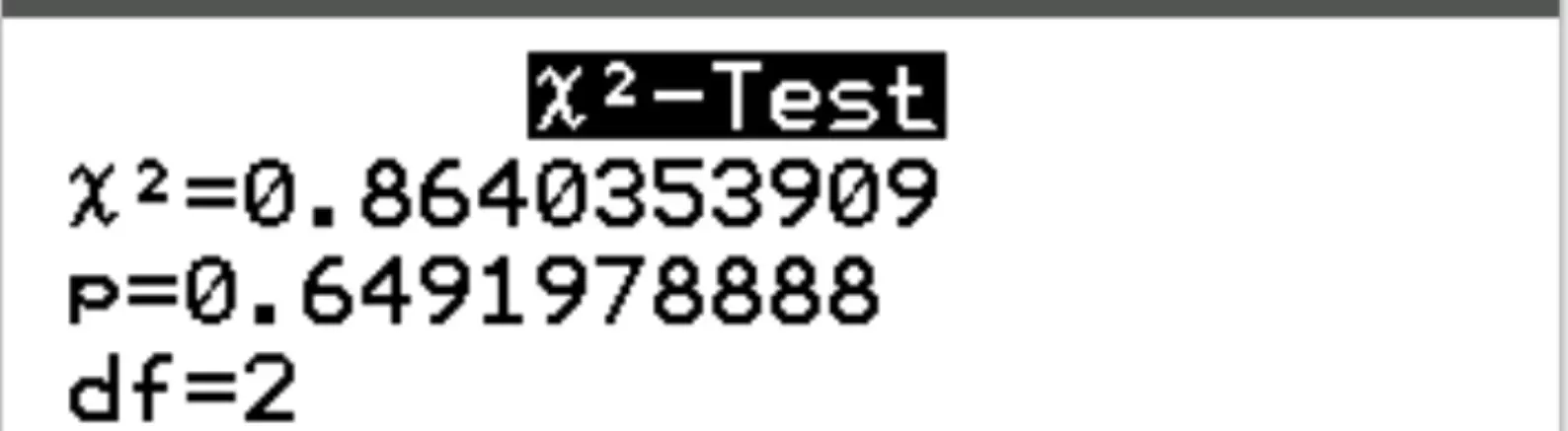
Etapa 3: interprete os resultados.
A estatística do teste X2 é 0,8640 e o valor p correspondente é 0,6492 . Como esse valor p não é inferior a 0,05, não rejeitamos a hipótese nula. Isto significa que não temos provas suficientes para afirmar que existe uma associação entre género e preferências partidárias.
About Author
Dr. benjamim anderson
Olá, sou Benjamin, um professor aposentado de estatística que se tornou professor dedicado na Statorials. Com vasta experiência e conhecimento na área de estatística, estou empenhado em compartilhar meu conhecimento para capacitar os alunos por meio de Statorials. Saber mais