Teste t de amostras pareadas: definição, fórmula e exemplo

Um teste t de amostras pareadas é usado para comparar as médias de duas amostras quando cada observação em uma amostra pode ser associada a uma observação na outra amostra.

Este tutorial explica o seguinte:

• A motivação para realizar um teste t de amostras pareadas.
• A fórmula para realizar um teste t de amostras pareadas.
• As suposições que devem ser atendidas para realizar um teste t de amostras pareadas.
• Um exemplo de como realizar um teste t de amostras pareadas.

Teste t de amostras pareadas: Motivação

Um teste t de amostras pareadas é comumente usado em dois cenários:

1. Uma medição é feita em um sujeito antes e depois de um tratamento – por exemplo, o salto vertical máximo de jogadores de basquete universitário é medido antes e depois de sua participação em um programa de treinamento.

2. Uma medição é feita sob duas condições diferentes – por exemplo, o tempo de resposta de um paciente é medido com dois medicamentos diferentes.

Em ambos os casos, queremos comparar a medição média entre dois grupos em que cada observação de uma amostra pode ser associada a uma observação da outra amostra.

Teste t de amostras pareadas: fórmula

Um teste t de amostras pareadas sempre usa a seguinte hipótese nula:

• H ₀ : μ ₁ = μ ₂ (as duas médias populacionais são iguais)

A hipótese alternativa pode ser bilateral, esquerda ou direita:

• H ₁ (bicaudal): μ ₁ ≠ μ ₂ (as médias das duas populações não são iguais)
• H ₁ (esquerda): μ ₁ < μ ₂ (a média da população 1 é inferior à média da população 2)
• H ₁ (direita): μ ₁ > μ ₂ (a média da população 1 é maior que a média da população 2)

Usamos a seguinte fórmula para calcular a estatística do teste t:

t = x _diferença / (s _diferença /√n)

Ouro:

• x _diff : exemplo de média das diferenças
• s: exemplo de desvio padrão de diferenças
• n: tamanho da amostra (ou seja, número de pares)

Se o valor p que corresponde à estatística do teste t com (n-1) graus de liberdade for menor que o nível de significância escolhido (as escolhas comuns são 0,10, 0,05 e 0,01), então você poderá rejeitar a hipótese nula.

Teste t de amostras pareadas: suposições

Para que os resultados de um teste t de amostras pareadas sejam válidos, as seguintes suposições devem ser atendidas:

• Os participantes devem ser selecionados aleatoriamente da população.
• As diferenças entre pares devem ser distribuídas aproximadamente normalmente.
• Não deve haver valores extremos nas diferenças.

Teste t de amostras pareadas : exemplo

Suponha que queiramos saber se um determinado programa de treinamento é capaz ou não de aumentar o salto vertical máximo (em polegadas) de jogadores de basquete universitário.

Para testar isso, podemos recrutar uma amostra aleatória simples de 20 jogadores de basquete universitário e medir cada um dos seus saltos verticais máximos. Depois podemos fazer com que cada jogador utilize o programa de treino durante um mês e depois medir novamente o seu salto vertical máximo no final do mês.

Para determinar se o programa de treinamento realmente teve efeito no salto vertical máximo, realizaremos um teste t de amostras pareadas no nível de significância α = 0,05 usando as seguintes etapas:

Etapa 1: Calcule os dados resumidos para as diferenças.

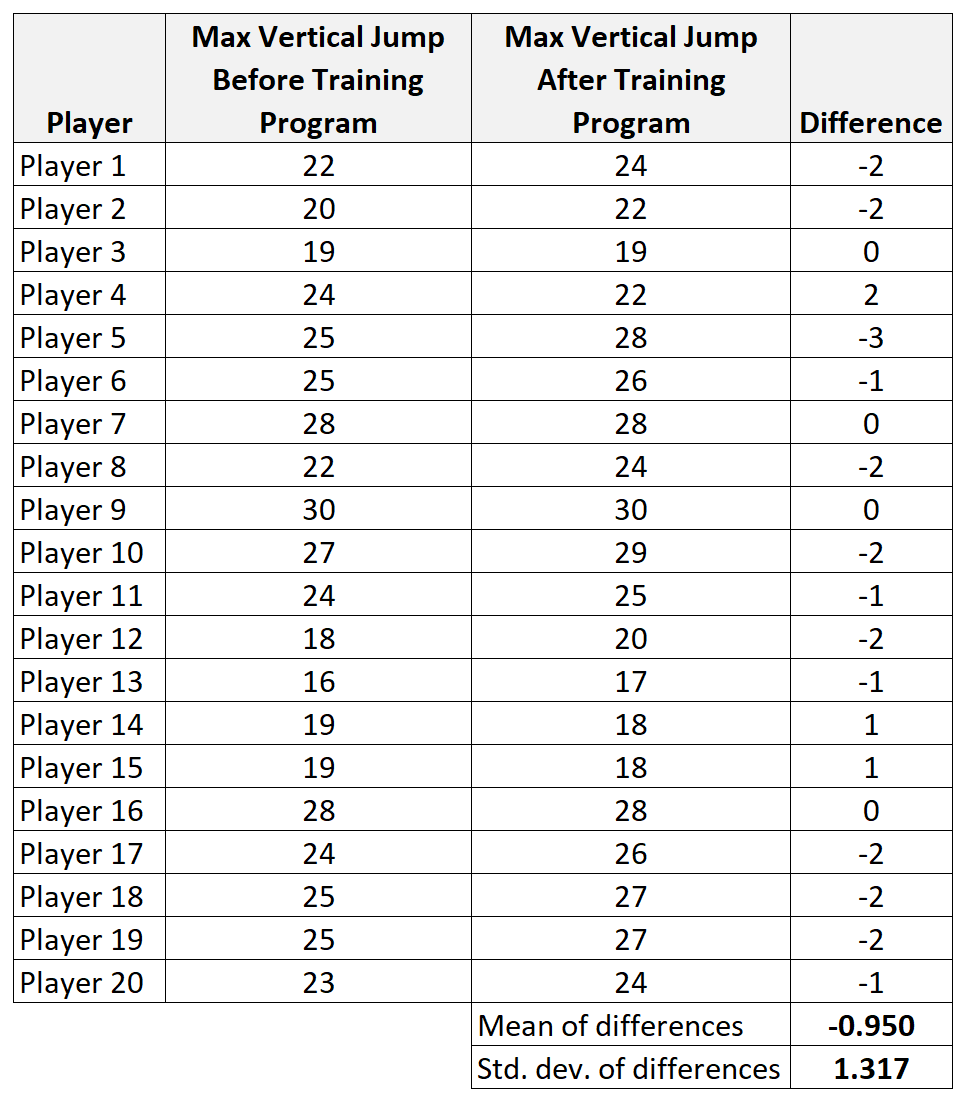
• x _diff : média amostral das diferenças = -0,95
• s: desvio padrão amostral das diferenças = 1,317
• n: tamanho da amostra (ou seja, número de pares) = 20

Etapa 2: Definir suposições.

Realizaremos o teste t para amostras pareadas com as seguintes hipóteses:

• H ₀ : μ ₁ = μ ₂ (as duas médias populacionais são iguais)
• H ₁ : μ ₁ ≠ μ ₂ (as duas médias populacionais não são iguais)

Etapa 3: Calcule a estatística do teste t .

t = x _diferença / (s _diferença /√n) = -0,95 / (1,317/ √ 20) = -3,226

Etapa 4: Calcule o valor p da estatística do teste t .

De acordo com a calculadora de pontuação T para valor P , o valor p associado a t = -3,226 e graus de liberdade = n-1 = 20-1 = 19 é 0,00445 .

Etapa 5: tire uma conclusão.

Como esse valor p está abaixo do nosso nível de significância α = 0,05, rejeitamos a hipótese nula. Temos evidências suficientes para dizer que a média do salto vertical máximo dos jogadores é diferente antes e depois de participarem do programa de treinamento.

Observação: você também pode realizar todo esse teste t de amostras pareadas simplesmente usando a calculadora de teste t de amostras pareadas .

Recursos adicionais

Os tutoriais a seguir explicam como realizar um teste t de amostras pareadas usando diferentes programas estatísticos:

Como realizar um teste t de amostras pareadas no Excel
Como realizar um teste t de amostras pareadas no SPSS
Como realizar um teste t de amostras pareadas no Stata
Como realizar um teste t de amostras emparelhadas em uma calculadora TI-84
Como realizar um teste t de amostras pareadas em R
Como realizar um teste t de amostras emparelhadas em Python
Como realizar um teste T de amostras emparelhadas manualmente