Compreendendo o teste t em regressão linear

A regressão linear é usada para quantificar a relação entre uma variável preditora e uma variável de resposta.

Sempre que realizamos uma regressão linear, queremos saber se existe uma relação estatisticamente significativa entre a variável preditora e a variável resposta.

Testamos a significância realizando um teste t para a inclinação da regressão. Usamos a seguinte hipótese nula e alternativa para este teste t:

• H ₀ : β ₁ = 0 (a inclinação é igual a zero)
• H _A : β ₁ ≠ 0 (a inclinação não é igual a zero)

Em seguida, calculamos a estatística de teste da seguinte forma:

t = b / SE _b

Ouro:

• b : estimativa do coeficiente
• SE _b : erro padrão da estimativa do coeficiente

Se o valor p que corresponde a t estiver abaixo de um determinado limite (por exemplo, α = 0,05), então rejeitamos a hipótese nula e concluímos que existe uma relação estatisticamente significativa entre a variável preditora e a variável resposta.

O exemplo a seguir mostra como realizar um teste t para um modelo de regressão linear na prática.

Exemplo: executando um teste t para regressão linear

Suponha que um professor queira analisar a relação entre as horas estudadas e as notas dos exames de 40 de seus alunos.

Realiza uma regressão linear simples usando horas estudadas como variável preditora e notas de exames recebidas como variável resposta.

A tabela a seguir mostra os resultados do modelo de regressão:

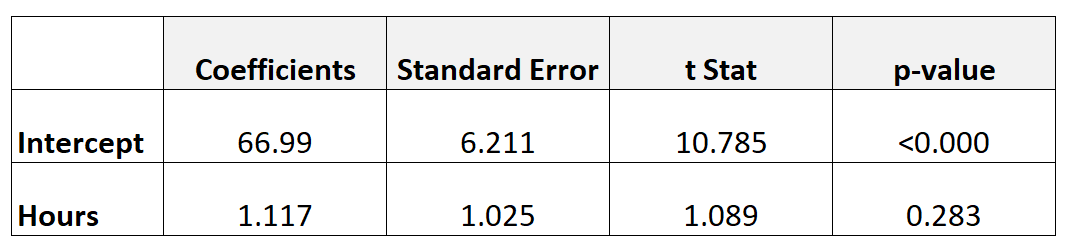
Para determinar se as horas estudadas têm relação estatisticamente significativa com a nota do exame final, podemos realizar um teste t.

Usamos a seguinte hipótese nula e alternativa para este teste t:

• H ₀ : β ₁ = 0 (a inclinação das horas estudadas é igual a zero)
• H _A : β ₁ ≠ 0 (a inclinação das horas estudadas não é igual a zero)

Em seguida, calculamos a estatística de teste da seguinte forma:

• t = b / SE _b
• t = 1,117 / 1,025
• t = 1,089

O valor p que corresponde a t = 1,089 com df = n-2 = 40 – 2 = 38 é 0,283 .

Observe que também podemos usar a calculadora de pontuação T para valor P para calcular este valor p:

Como esse valor p não é inferior a 0,05, não rejeitamos a hipótese nula.

Isso significa que as horas estudadas não apresentam relação estatisticamente significativa entre os resultados dos exames finais.

Recursos adicionais

Os tutoriais a seguir fornecem informações adicionais sobre regressão linear:

Introdução à regressão linear simples
Introdução à regressão linear múltipla
Como interpretar coeficientes de regressão
Como interpretar o teste F para significância geral na regressão