Teste t de estudante

By Dr. benjamim anderson Agosto 3, 2023 Estatisticas 0 Comments

Este artigo explica o que é o teste t de Student e para que ele é usado em estatística. Assim, você descobrirá como é realizado o teste t de Student, quais são os diferentes tipos de testes t de Student e a fórmula de cada um.

O que é o teste t de Student?

O teste t de Student , também chamado de teste T ou simplesmente teste t , é um teste estatístico em que a estatística do teste segue a distribuição t de Student . Portanto, em estatística, o teste t de Student é usado para rejeitar ou aceitar a hipótese nula de um teste de hipótese.

Especificamente, o teste t de Student é usado em testes de hipóteses nos quais a população estudada segue uma distribuição normal, mas o tamanho da amostra é muito pequeno para conhecer a variância da população.

Resumindo, o teste t de Student é utilizado para rejeitar ou aceitar a hipótese de estudo de determinados testes de hipóteses. Por exemplo, o teste t de Student é usado para testar hipóteses para uma amostra, para amostras independentes ou para amostras relacionadas. Veremos então como o teste t de Student é calculado em cada caso.

Tipos de testes t de Student

Existem três tipos de testes t de Student :

Teste t de Student para uma amostra – é usado para testar a hipótese sobre o valor da média amostral.
Teste t de Student para duas amostras independentes : permite testar a hipótese sobre a diferença entre as médias de duas amostras independentes.
Teste t de Student para duas amostras pareadas (ou amostras relacionadas) – é usado para investigar a hipótese sobre a média de uma amostra testada duas vezes.

Uma amostra do teste t de Student

Os testes de hipóteses para a média amostral são aqueles em que a hipótese nula e a hipótese alternativa do teste dizem algo sobre o valor da média populacional.

A fórmula para o teste t de Student para uma amostra é a seguinte:

$\displaystyle t=\frac{\overline{x}-\mu}{\displaystyle \frac{s}{\sqrt{n}}}$

Ouro:

$t$

é a estatística do teste de hipótese para a média, que é definida pela distribuição t de Student.
$\overline{x}$

é a média amostral.
$\mu$

é o valor da média proposta no teste de hipótese.
$s$

é o desvio padrão da amostra.
$n$

é o tamanho da amostra.

Uma vez calculado o valor do teste t de Student, o resultado do teste estatístico com o valor crítico deve ser interpretado para rejeitar ou não a hipótese nula:

Se o teste de hipótese para a média for bilateral, a hipótese nula é rejeitada se o valor absoluto do teste t de Student for maior que o valor crítico t _α/2|n-1 .
Se o teste de hipótese para a média corresponder à cauda direita, a hipótese nula será rejeitada se o valor do teste t de Student for maior que o valor crítico t _α|n-1 .
Se o teste de hipótese para a média corresponder à cauda esquerda, a hipótese nula será rejeitada se o valor do teste t de Student for menor que o valor crítico -t _α|n-1 .

$\begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |t|>t_{\alpha/2|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t>t_{\alpha|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t<-t_{\alpha|n-1} \text{ se rechaza } H_0\end{array}$

Observe que os valores críticos do teste são obtidos na tabela de distribuição de Student.

➤ Veja: Exemplo concreto de teste de hipótese para a média

Teste t de Student para amostras independentes

O teste t de Student para amostras independentes é utilizado para rejeitar ou aceitar a hipótese de relação entre as médias de duas populações, por exemplo, que as médias de duas populações são diferentes ou que a média da população A é maior que a média de . população B.

No entanto, neste caso, a fórmula do teste t de Student varia dependendo se as variâncias populacionais podem ser consideradas iguais ou não. Veremos então os dois casos possíveis.

Desvios desconhecidos e iguais

A fórmula para calcular o teste t de Student para amostras independentes quando as variâncias da população são desconhecidas, mas consideradas iguais, é a seguinte:

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$

Ouro:

$t$

é a estatística de teste de hipótese para a diferença de médias com variâncias desconhecidas, que segue uma distribuição t de Student com n ₁ + n ₂ -2 graus de liberdade.
$\mu_1$

é a média da população 1.
$\mu_2$

é a média da população 2.
$\overline{x_1}$

é a média da amostra 1.
$\overline{x_2}$

é a média da amostra 2.
$s_p$

é o desvio padrão combinado.
$n_1$

é o tamanho da amostra 1.
$n_2$

é o tamanho da amostra 2.

O desvio padrão combinado das duas amostras é calculado usando a seguinte fórmula:

$\displaystyle s_p=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}$

Variações desconhecidas e diferentes

Quando as variâncias populacionais são desconhecidas e, além disso, assumidas como diferentes, a fórmula de cálculo do teste t de Student para amostras independentes é a seguinte:

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle \sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}}$

Ouro:

$t$

é a estatística de teste de hipótese para a diferença de médias com variâncias desconhecidas, que segue uma distribuição t de Student.
$\mu_1$

é a média da população 1.
$\mu_2$

é a média da população 2.
$\overline{x_1}$

é a média da amostra 1.
$\overline{x_2}$

é a média da amostra 2.
$\sigma_1$

é o desvio padrão da população 1.
$\sigma_2$

é o desvio padrão da população 2.
$n_1$

é o tamanho da amostra 1.
$n_2$

é o tamanho da amostra 2.

Porém, neste caso, os graus de liberdade da distribuição t de Student são calculados pela seguinte fórmula:

$\displaystyle GL=\frac{\displaystyle\left(\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}\right)^2}{\displaystyle\frac{\displaystyle\frac{s_1^2}{n_1}}{n_1-1}+\frac{\displaystyle\frac{s_2^2}{n_2}}{n_2-1}}$

➤ Veja: Exemplo concreto de teste de hipótese para diferença de médias

Teste t de Student para amostras pareadas ou relacionadas

Este teste é utilizado quando duas amostras em estudo estão relacionadas entre si, de modo que se trata, na verdade, de uma única amostra de indivíduos que foi analisada duas vezes (cada vez em condições diferentes).

Por exemplo, você pode analisar as notas dos alunos em um curso de matemática e estatística para ver se há uma diferença significativa entre as médias das duas disciplinas. Nesse caso, a nota de matemática de cada aluno está vinculada à nota de estatística desse mesmo aluno.

A fórmula do teste t de Student para amostras pareadas ou relacionadas é:

$\displaystyle t=\frac{\overline{x_D}-\mu_D}{\displaystyle \frac{s_D}{\sqrt{n}}}$

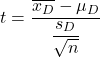
Ouro:

$t$

é a estatística de teste de hipótese para médias pareadas, que é definida pela distribuição t de Student.
$\overline{x_D}$

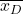
é a média da amostra formada pela diferença nos dados.
$\mu_D$

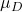
é o valor da média proposta no teste de hipótese.
$s_D$

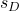
é o desvio padrão da amostra formada pela diferença nos dados.
$n$

é o tamanho da amostra.

Suposições do teste t de Student

Para realizar o teste t de Student, as seguintes condições devem ser atendidas:

Continuidade – Os dados da amostra são contínuos.
Aleatoriedade : as amostras de dados foram selecionadas aleatoriamente.
Homogeneidade : A variância da amostra de dados é homogênea.
Normalidade – A distribuição que define a amostra de dados é aproximadamente normal.

Como fazer um teste t de Student

Finalmente, em resumo, são detalhados os passos a seguir para realizar um teste t de Student.

Defina as hipóteses nula e alternativa do teste de hipóteses.
Estabeleça o nível de significância (α) do teste de hipótese.
Verifique se as suposições do teste t de Student foram atendidas.
Aplique a fórmula do teste t de Student correspondente e calcule a estatística do teste.
Interprete o resultado do teste t de Student comparando-o com o valor crítico do teste.

About Author

Dr. benjamim anderson

Olá, sou Benjamin, um professor aposentado de estatística que se tornou professor dedicado na Statorials. Com vasta experiência e conhecimento na área de estatística, estou empenhado em compartilhar meu conhecimento para capacitar os alunos por meio de Statorials. Saber mais

O que é o teste t de Student?

Tipos de testes t de Student

Uma amostra do teste t de Student

Teste t de Student para amostras independentes

Desvios desconhecidos e iguais

Variações desconhecidas e diferentes

Teste t de Student para amostras pareadas ou relacionadas

Suposições do teste t de Student

Como fazer um teste t de Student

About Author

Dr. benjamim anderson

Add a Comment