Como realizar uma transformação box-cox em r (com exemplos)

Uma transformação box-cox é um método comumente usado para transformar um conjunto de dados distribuído não normalmente em um conjunto distribuído mais normalmente .

A ideia básica por trás deste método é encontrar um valor para λ tal que os dados transformados estejam o mais próximo possível da distribuição normal, usando a seguinte fórmula:

• y(λ) = (y ^λ – 1) / λ se y ≠ 0
• y(λ) = log(y) se y = 0

Podemos realizar uma transformação box-cox em R usando a função boxcox() da biblioteca MASS() . O exemplo a seguir mostra como usar esta função na prática.

Consulte este artigo da Universidade de Connecticut para obter um bom resumo do desenvolvimento da transformação Box-Cox.

Exemplo: Transformação Box-Cox em R

O código a seguir mostra como ajustar um modelo de regressão linear a um conjunto de dados e, em seguida, usar a função boxcox() para encontrar um lambda ideal para transformar a variável de resposta e ajustar um novo modelo.

 library (MASS)

#create data
y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8)
x=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8)

#fit linear regression model
model <- lm(y~x)

#find optimal lambda for Box-Cox transformation 
bc <- boxcox(y ~ x)
(lambda <- bc$x[which.max(bc$y)])

[1] -0.4242424

#fit new linear regression model using the Box-Cox transformation
new_model <- lm(((y^lambda-1)/lambda) ~ x)

O lambda ideal acabou sendo -0.4242424 . Assim, o novo modelo de regressão substituiu a variável resposta original y pela variável y = (y ^-0,4242424 – 1) / -0,4242424.

O código a seguir mostra como criar dois gráficos QQ em R para visualizar as diferenças nos resíduos entre os dois modelos de regressão:

 #define plotting area
op <- par(pty = "s", mfrow = c(1, 2))

#QQ plot for original model
qqnorm(model$residuals)
qqline(model$residuals)

#QQ plot for Box-Cox transformed model
qqnorm(new_model$residuals)
qqline(new_model$residuals)

#display both QQ plots
by(op)

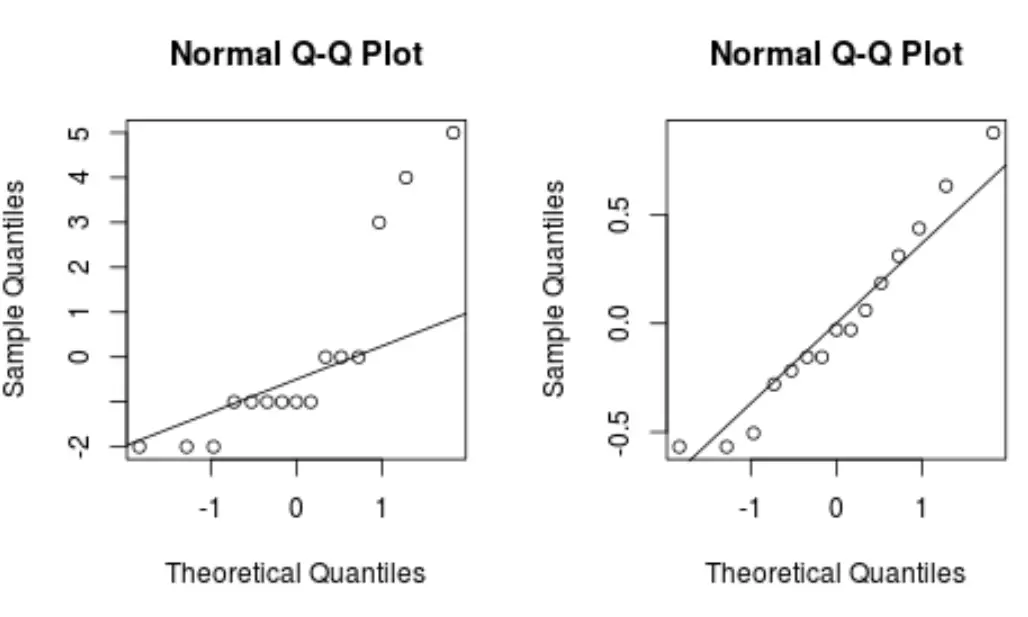
Geralmente, se os pontos de dados estiverem ao longo de uma linha diagonal reta em um gráfico QQ, o conjunto de dados provavelmente segue uma distribuição normal.

Observe como o modelo transformado box-cox produz um gráfico QQ com uma linha muito mais reta do que o modelo de regressão original.

Isto indica que os resíduos do modelo transformado box-cox são distribuídos muito mais normalmente, o que satisfaz um dos pressupostos da regressão linear .

Recursos adicionais

Como transformar dados em R (Log, raiz quadrada, raiz cúbica)
Como criar e interpretar um gráfico QQ em R
Como realizar um teste de Shapiro-Wilk para normalidade em R