Como transformar dados em r (log, raiz quadrada, raiz cúbica)

Muitos testes estatísticos assumem que os resíduos de uma variável de resposta são normalmente distribuídos.

No entanto, os resíduos muitas vezes não são normalmente distribuídos. Uma maneira de resolver este problema é transformar a variável de resposta usando uma das três transformações:

1. Transformação de log: transforme a variável de resposta de y em log(y) .

2. Transformação de raiz quadrada: Transforme a variável de resposta de y em √y .

3. Transformação da raiz cúbica: transforme a variável de resposta de y em y ^1/3 .

Ao realizar essas transformações, a variável resposta geralmente se aproxima da distribuição normal. Os exemplos a seguir mostram como realizar essas transformações em R.

Transformação de log em R

O código a seguir mostra como executar uma transformação de log em uma variável de resposta:

 #create data frame
df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8),
                 x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8),
                 x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7))

#perform log transformation
log_y <- log10(df$y)

O código a seguir mostra como criar histogramas para exibir a distribuição de y antes e depois de realizar uma transformação de log:

 #create histogram for original distribution
hist(df$y, col='steelblue', main='Original')

#create histogram for log-transformed distribution 
hist(log_y, col='coral2', main='Log Transformed')

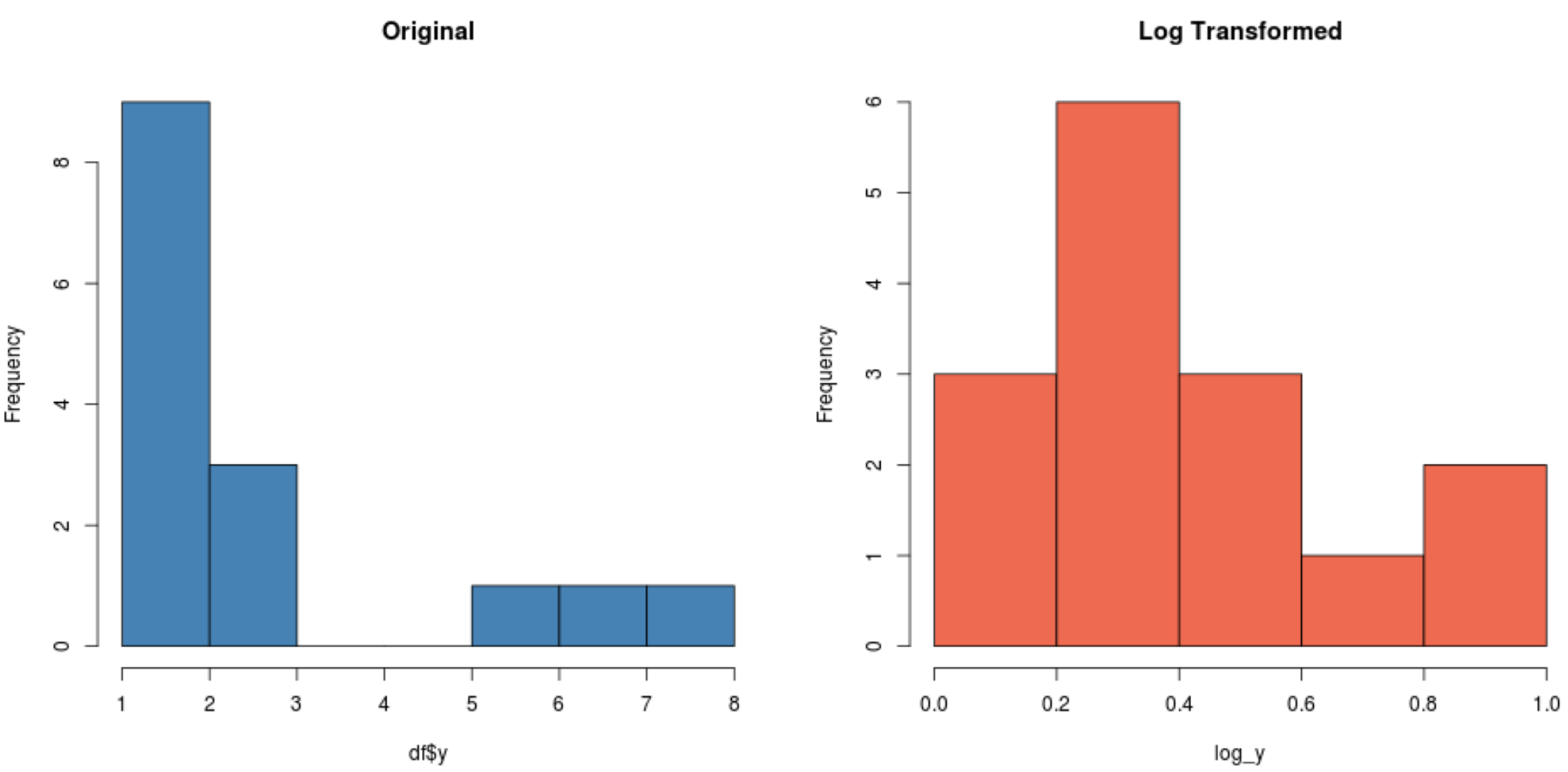
Observe como a distribuição transformada em logaritmo é muito mais normal do que a distribuição original. Ainda não tem um “formato de sino” perfeito, mas está mais próximo de uma distribuição normal do que da distribuição original.

Na verdade, se realizarmos umteste de Shapiro-Wilk em cada distribuição, descobriremos que a distribuição original falha na suposição de normalidade, enquanto a distribuição transformada em logaritmo não (em α = 0,05):

 #perform Shapiro-Wilk Test on original data
shapiro.test(df$y)

	Shapiro-Wilk normality test

data: df$y
W = 0.77225, p-value = 0.001655

#perform Shapiro-Wilk Test on log-transformed data 
shapiro.test(log_y)

	Shapiro-Wilk normality test

data:log_y
W = 0.89089, p-value = 0.06917

Transformação de raiz quadrada em R

O código a seguir mostra como realizar uma transformação de raiz quadrada em uma variável de resposta:

 #create data frame
df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8),
                 x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8),
                 x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7))

#perform square root transformation
sqrt_y <- sqrt(df$y)

O código a seguir mostra como criar histogramas para exibir a distribuição de y antes e depois de realizar uma transformação de raiz quadrada:

 #create histogram for original distribution
hist(df$y, col='steelblue', main='Original')

#create histogram for square root-transformed distribution 
hist(sqrt_y, col='coral2', main='Square Root Transformed') 

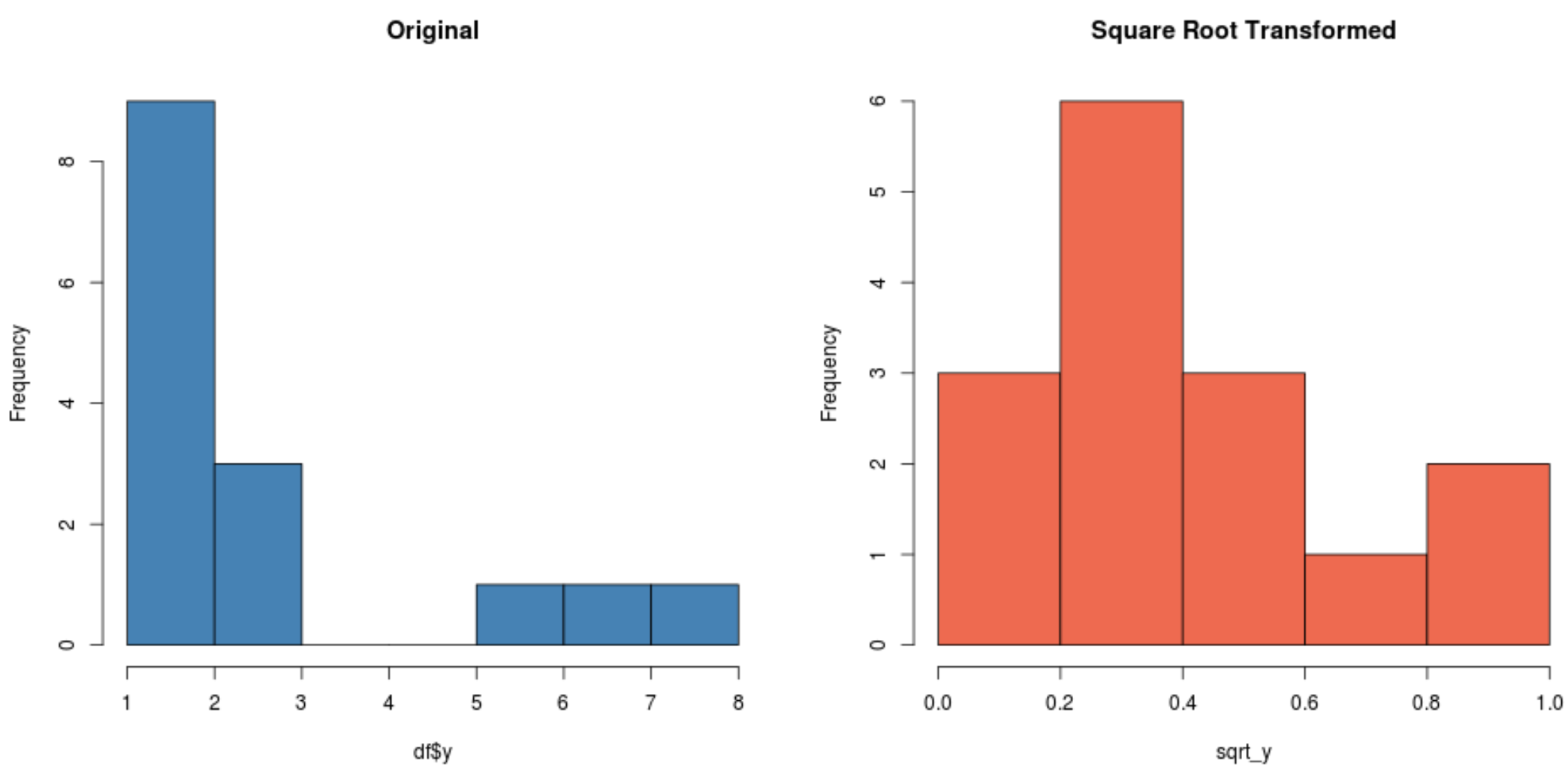
Observe como a distribuição transformada pela raiz quadrada é distribuída muito mais normalmente do que a distribuição original.

Transformação de raiz cúbica em R

O código a seguir mostra como executar uma transformação de raiz cúbica em uma variável de resposta:

 #create data frame
df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8),
                 x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8),
                 x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7))

#perform square root transformation
cube_y <- df$y^(1/3)

O código a seguir mostra como criar histogramas para exibir a distribuição de y antes e depois de realizar uma transformação de raiz quadrada:

 #create histogram for original distribution
hist(df$y, col='steelblue', main='Original')

#create histogram for square root-transformed distribution 
hist(cube_y, col='coral2', main='Cube Root Transformed') 

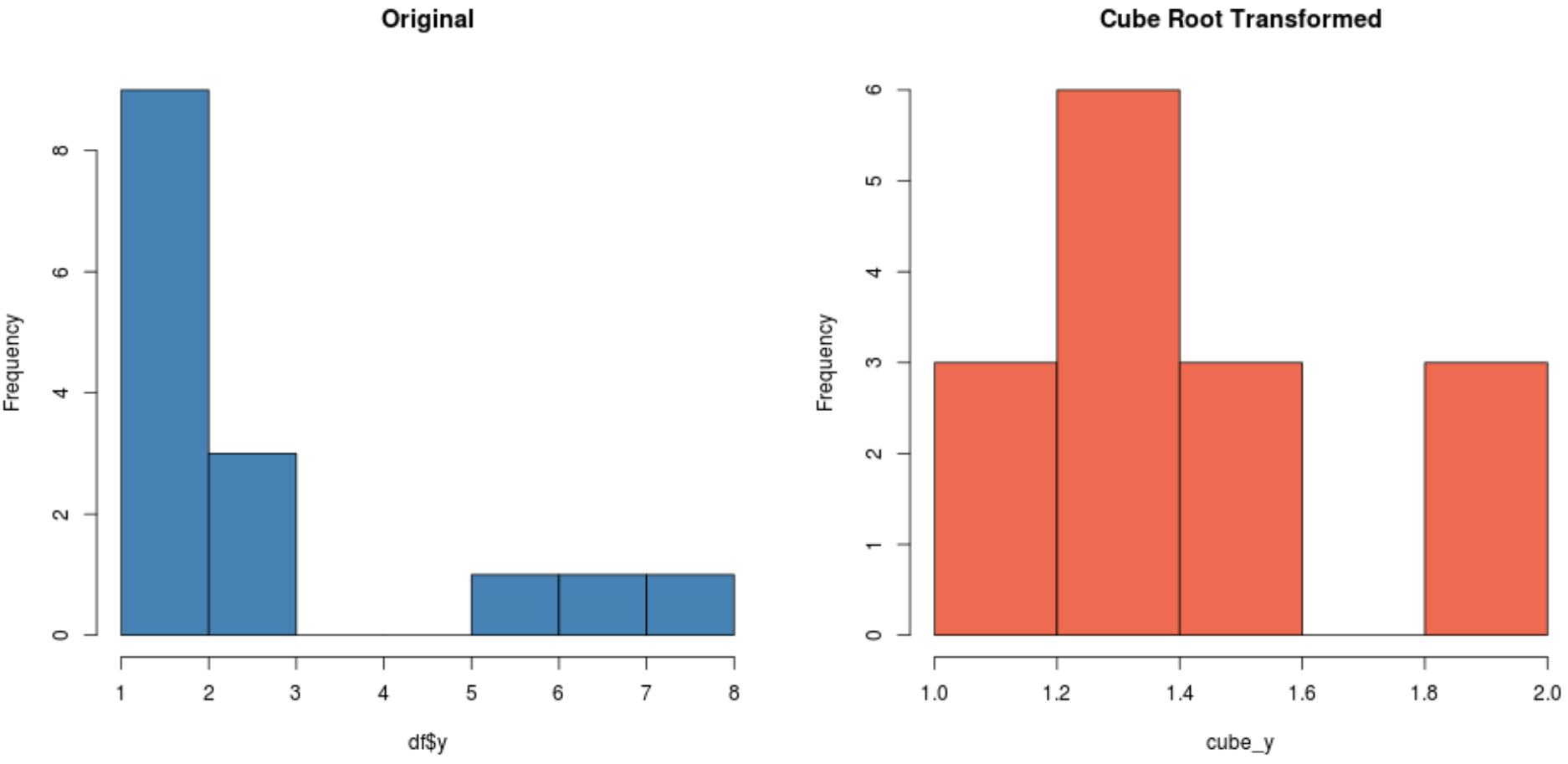
Dependendo do seu conjunto de dados, uma dessas transformações pode produzir um novo conjunto de dados com distribuição mais normal do que os outros.