Como realizar um teste t de uma amostra em uma calculadora ti-84

Um teste t de uma amostra é usado para testar se a média de uma população é ou não igual a um determinado valor.

Este tutorial explica como realizar um teste t de uma amostra em uma calculadora TI-84.

Exemplo: um teste t de amostra em uma calculadora TI-84

Os pesquisadores querem saber se um determinado tipo de carro atinge ou não uma velocidade de 20 milhas por galão. Eles obtêm uma amostra aleatória de 74 carros e descobrem que a média é de 21,29 mpg, enquanto o desvio padrão é de 5,78 mpg. Use esses dados para realizar um teste t de uma amostra para determinar se o verdadeiro mpg para este tipo de carro é igual a 20 mpg.

Etapa 1: selecione Teste T.

Toque em Estatística . Role para baixo até TESTES. Vá até Teste T e pressione ENTER .

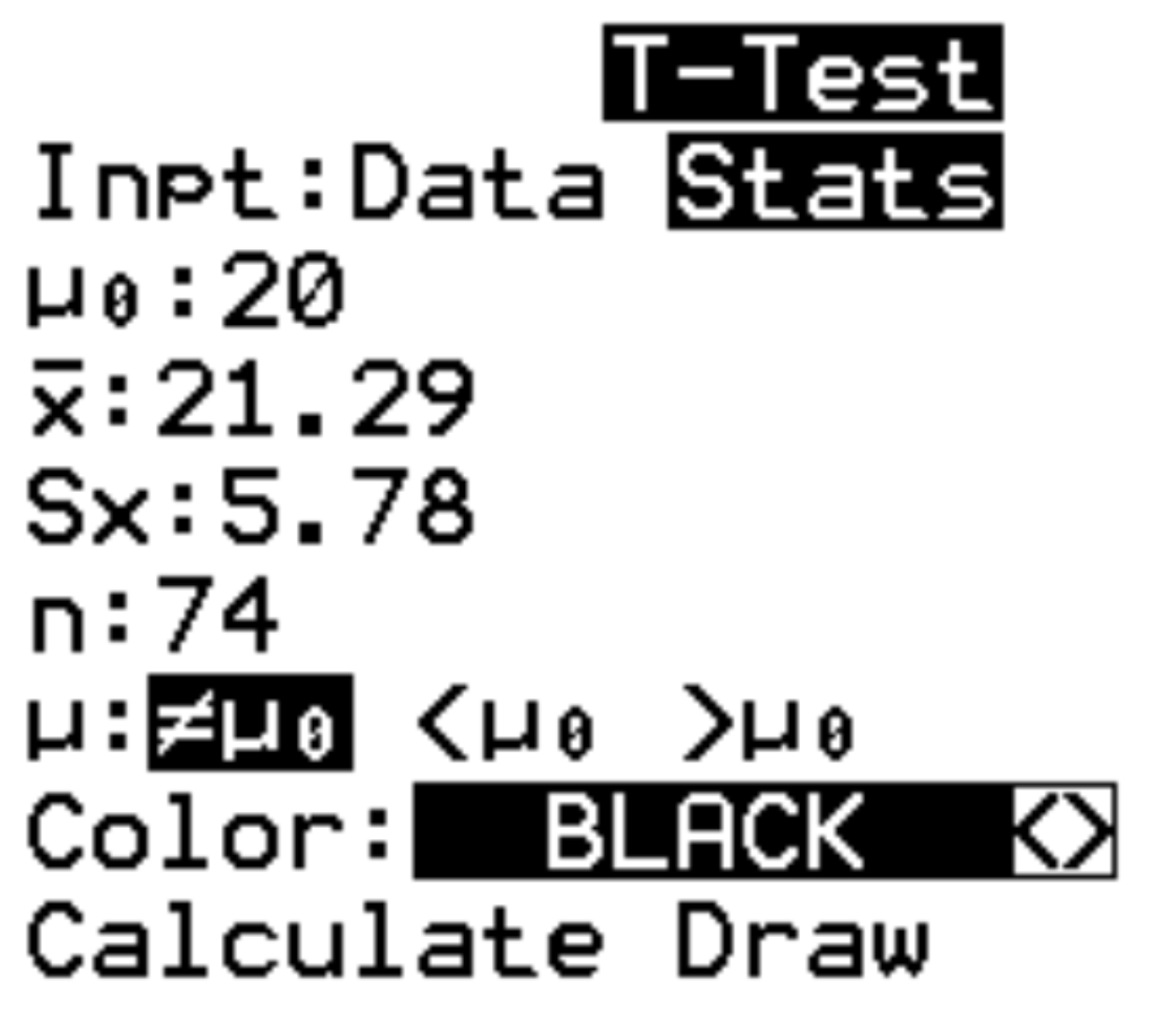
Passo 2: Preencha as informações necessárias.

A calculadora solicitará as seguintes informações:

• Entrada: escolha se você está trabalhando com dados brutos (Dados) ou estatísticas resumidas (Estatísticas). Neste caso iremos destacar Stats e pressionar ENTER .
• μ ₀ : A média a ser usada na hipótese nula. Digitaremos 20 e pressionaremos ENTER .
• x : A amostra significa. Digitaremos 21.29 e pressionaremos ENTER .
• s _x : O desvio padrão da amostra. Digitaremos 5.78 e pressionaremos ENTER .
• n : O tamanho da amostra. Digitaremos 74 e pressionaremos ENTER .
• μ : A hipótese alternativa a ser usada. Como estamos realizando um teste bicaudal, destacaremos ≠ μ ₀ e pressionaremos ENTER . Isso indica que nossa hipótese alternativa é μ≠20. As outras duas opções seriam usadas para testes à esquerda (<μ ₀ ) e testes à direita (>μ ₀ ) .

Por fim, destaque Calcular e pressione ENTER .

Etapa 3: interprete os resultados.

Nossa calculadora produzirá automaticamente os resultados do teste t de uma amostra:

Veja como interpretar os resultados:

• μ≠20 : Esta é a hipótese alternativa do teste.
• t=1,919896124 : Esta é a estatística do teste t.
• p=0,0587785895 : Este é o valor p que corresponde à estatística de teste.
• x =21,59 . Esta é a amostra média que capturamos.
• _sx =5,78 . Este é o desvio padrão da amostra que inserimos.
• n=74 : Este é o tamanho da amostra que inserimos.

Como o valor p do teste (0,0587785895) não é inferior a 0,05, não rejeitamos a hipótese nula. Isso significa que não temos evidências suficientes para dizer que o mpg médio para esse tipo de carro seja diferente de 20 mpg.