Um z-score pode ser negativo?

Nas estatísticas, uma pontuação z nos diz quantos desvios padrão um valor está da média . Usamos a seguinte fórmula para calcular uma pontuação z:

z = (X – μ) / σ

onde X é o valor que estamos analisando, μ é a média e σ é o desvio padrão.

Uma pontuação z pode ser positiva, negativa ou zero.

Uma pontuação z positiva indica que um determinado valor está acima da média, uma pontuação z negativa indica que um determinado valor está abaixo da média e uma pontuação z zero indica que um determinado valor é igual à média.

Alguns exemplos devem deixar isso claro.

Exemplos: Calculando uma pontuação Z

Digamos que temos o seguinte conjunto de dados que mostra a altura (em polegadas) de um determinado grupo de plantas:

5, 7, 7, 8, 9, 10, 13, 17, 17, 18, 19, 19, 20

A média amostral deste conjunto de dados é 13 e o desvio padrão amostral é 5,51 .

1. Encontre a pontuação z para o valor “8” neste conjunto de dados.

Veja como calcular a pontuação z:

z = (X – μ) / σ = (8 – 13) / 5,51 = -0,91

Isso significa que o valor “8” é 0,91 desvios padrão inferior à média.

2. Encontre a pontuação z para o valor “13” neste conjunto de dados.

Veja como calcular a pontuação z:

z = (X – μ) / σ = (13 – 13) / 5,46 = 0

Isso significa que o valor “13” é exatamente igual à média.

3. Encontre a pontuação z para o valor “20” neste conjunto de dados.

Veja como calcular a pontuação z:

z = (X – μ) / σ = (20 – 13) / 5,46 = 1,28

Isto significa que o valor “20” está 1,28 desvios padrão acima da média.

Como interpretar pontuações Z

O gráfico AZ nos informa qual porcentagem de valores fica abaixo de determinadas pontuações Z. Alguns exemplos devem deixar isso claro.

Exemplo 1: pontuações Z negativas

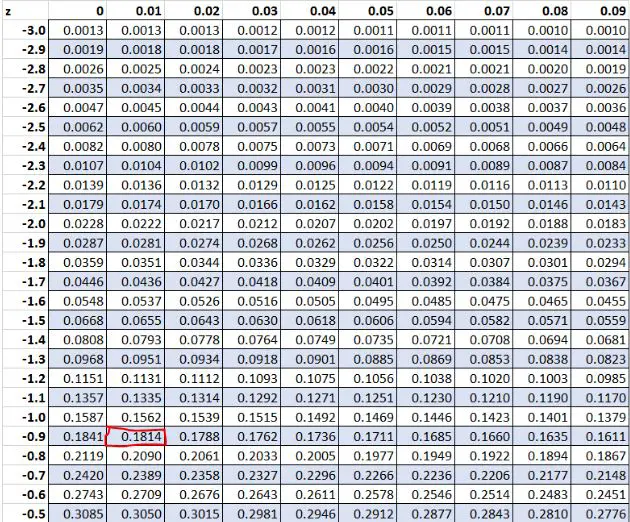
Anteriormente, descobrimos que o valor bruto “8” em nosso conjunto de dados tinha uma pontuação z de -0,91 . Segundo a tabela Z, 18,14% dos valores são inferiores a este valor.

Exemplo 2: Z-Scores iguais a zero

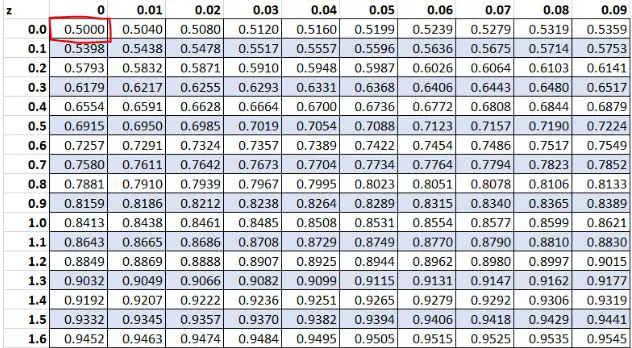
Anteriormente, descobrimos que o valor bruto “13” em nosso conjunto de dados tinha uma pontuação z de 0 . De acordo com a tabela Z, 50,00% dos valores são inferiores a este valor.

Exemplo 3: pontuações Z positivas

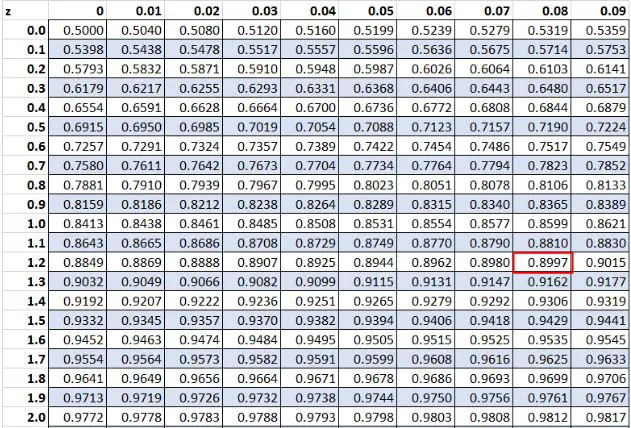
Anteriormente, descobrimos que o valor bruto “20” em nosso conjunto de dados tinha uma pontuação z de 1,28 . Segundo a tabela Z, 89,97% dos valores são inferiores a este valor.

Conclusão

As pontuações Z podem assumir qualquer valor entre o infinito negativo e o infinito positivo, mas a maioria das pontuações z está dentro de 2 desvios padrão da média. Na verdade, existe uma regra em estatística conhecida como regra prática , que afirma que, para um determinado conjunto de dados com distribuição normal:

• 68% dos valores dos dados estão dentro de um desvio padrão da média.
• 95% dos valores dos dados estão dentro de dois desvios padrão da média.
• 99,7% dos valores dos dados estão dentro de três desvios padrão da média.

Quanto maior o valor absoluto de uma pontuação z, mais distante o valor bruto está da média do conjunto de dados. Quanto menor o valor absoluto de uma pontuação z, mais próximo o valor bruto está da média do conjunto de dados.

Tópicos relacionados:

Calculadora de regras práticas
Como aplicar a regra prática no Excel