Como realizar anova unidirecional no excel

Uma ANOVA unidirecional (“análise de variância”) é usada para determinar se há ou não uma diferença estatisticamente significativa entre as médias de três ou mais grupos independentes.

Este tutorial explica como realizar uma ANOVA unidirecional no Excel.

Exemplo: ANOVA unidirecional no Excel

Suponha que um pesquisador recrute 30 estudantes para participar de um estudo. Os alunos são designados aleatoriamente para usar uma das três técnicas de estudo nas próximas três semanas para se prepararem para um exame. No final das três semanas, todos os alunos fazem o mesmo teste.

Os resultados dos testes dos alunos são mostrados abaixo:

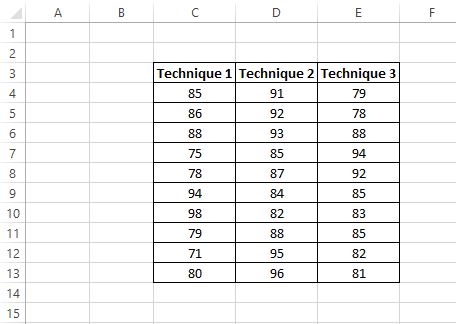
O pesquisador deseja realizar uma ANOVA unidirecional para determinar se as pontuações médias são iguais nos três grupos.

Para realizar ANOVA unidirecional no Excel, vá até a aba Dados e clique na opção Análise de Dados no grupo Análise .

Se você não vir a opção Análise de dados , primeiro deverá carregar o software gratuito Analysis ToolPak .

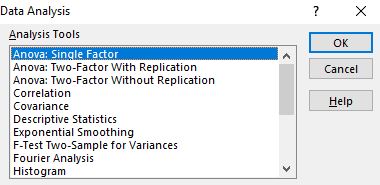
Depois de clicar nele, uma janela aparecerá com diferentes opções de ferramentas de verificação. Selecione Anova: fator único e clique em OK .

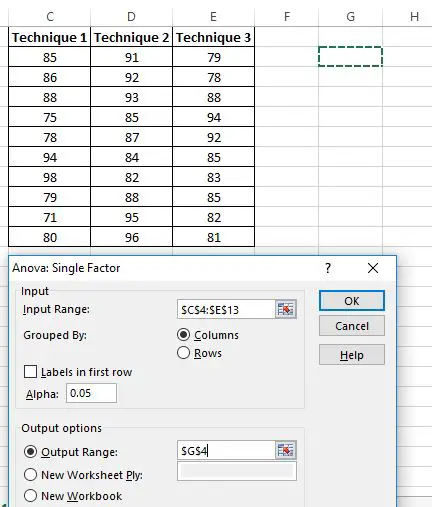
Uma nova janela aparece solicitando um intervalo de entrada . Você pode arrastar uma caixa ao redor dos seus dados ou inserir manualmente o intervalo de dados. Neste caso, nossos dados estão nas células C4:E13 .

A seguir, escolha um nível Alpha para o teste. Por padrão, esse número é 0,05. Neste caso, deixarei em 0,05.

Por fim, escolha uma célula para o Output Range , onde aparecerão os resultados da ANOVA unidirecional. Neste caso, escolho a célula G4 .

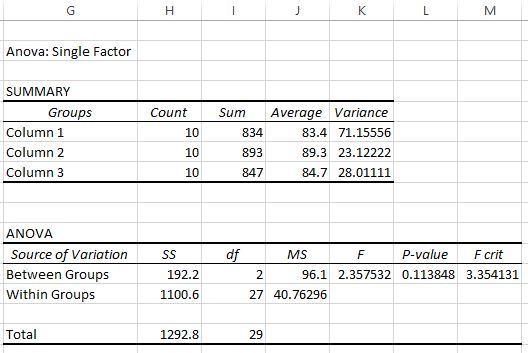
Depois de clicar em OK , o resultado da ANOVA unidirecional aparecerá:

Interpretação do resultado

Duas tabelas são exibidas na saída. A primeira é uma tabela de resumo que mostra o número de pontuações dos testes em cada grupo, a soma das pontuações dos testes, a média das pontuações dos testes e a variância das pontuações dos testes.

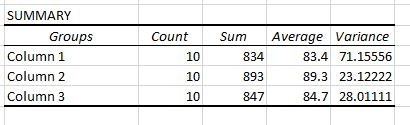
Lembre-se de que uma ANOVA unidirecional é usada para determinar se há ou não uma diferença estatisticamente significativa entre as médias de três ou mais grupos.

Nesta primeira tabela podemos ver que a pontuação média para cada um dos três grupos é diferente, mas para saber se estas diferenças são estatisticamente significativas precisamos de olhar para a segunda tabela.

A segunda tabela mostra a estatística do teste F, o valor crítico de F e o valor de p:

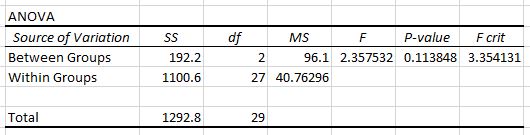
Neste caso, a estatística do teste F é 2,3575 e o valor crítico de F é 3,3541 . Como a estatística do teste F é menor que o valor crítico de F, não temos evidências suficientes para rejeitar a hipótese nula de que as médias dos três grupos são iguais.

Isto significa que não temos evidências suficientes para dizer que há uma diferença nos resultados dos testes entre as três técnicas de estudo.

Também poderíamos usar o valor p para chegar à mesma conclusão. Nesse caso, o valor p é 0,1138 , que é superior ao nível alfa de 0,05 .

Isto significa que não temos provas suficientes para rejeitar a hipótese nula de que as médias dos três grupos são iguais.

Nota: Nos casos em que você rejeita a hipótese nula, você pode realizar um teste post hoc de Tukey-Kramer para determinar exatamente quais médias de grupo são diferentes.