Como realizar anova unidirecional no spss

Uma ANOVA unidirecional é usada para determinar se há ou não uma diferença estatisticamente significativa entre as médias de três ou mais grupos independentes.

Esse tipo de teste é chamado de ANOVA unidirecional porque analisamos o impacto de uma variável preditora em uma variável de resposta.

Se, em vez disso, estivéssemos interessados no impacto de duas variáveis preditoras em uma variável de resposta, poderíamos realizar uma ANOVA bidirecional .

Este tutorial explica como realizar uma ANOVA unidirecional no SPSS.

Exemplo: ANOVA unidirecional no SPSS

Suponha que um pesquisador recrute 30 estudantes para participar de um estudo. Os alunos são designados aleatoriamente para usar uma das três técnicas de estudo no mês seguinte para se prepararem para um exame. No final do mês, todos os alunos fazem o mesmo teste.

Os resultados dos testes dos alunos são mostrados abaixo:

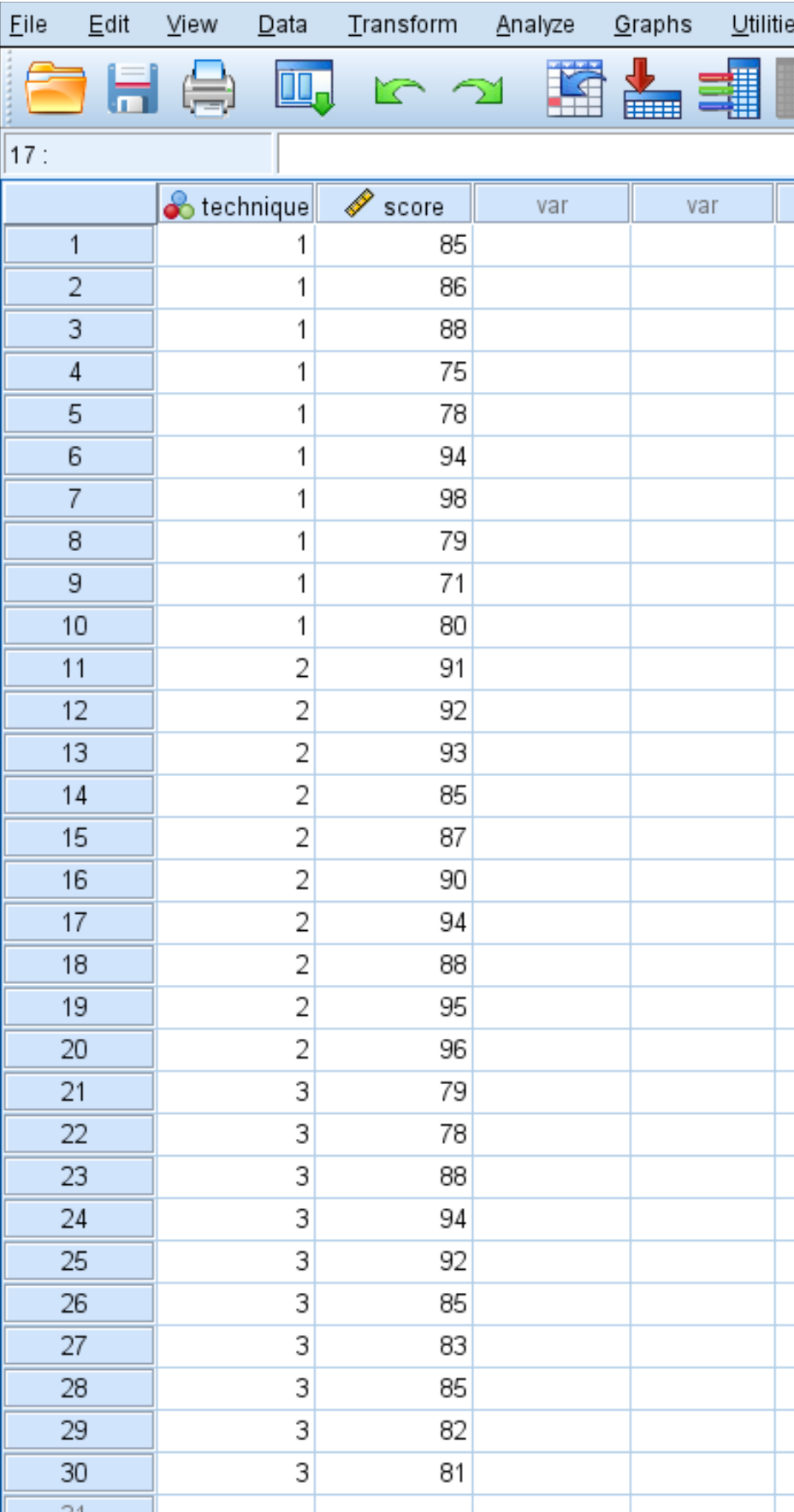
Use as etapas a seguir para realizar uma ANOVA unidirecional para determinar se as pontuações médias são iguais nos três grupos.

Etapa 1: visualize os dados.

Primeiro, criaremos boxplots para visualizar a distribuição das pontuações dos testes para cada uma das três técnicas de estudo. Clique na guia Gráficos e em Construtor de Gráficos .

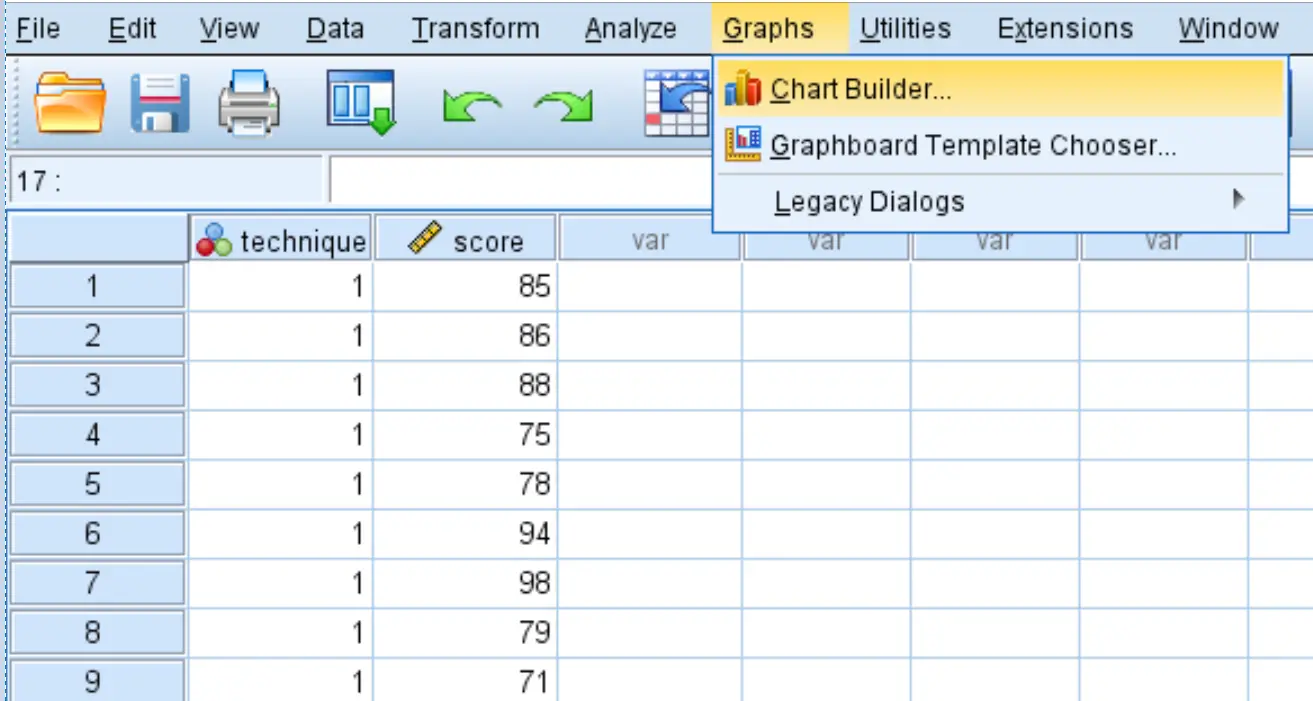
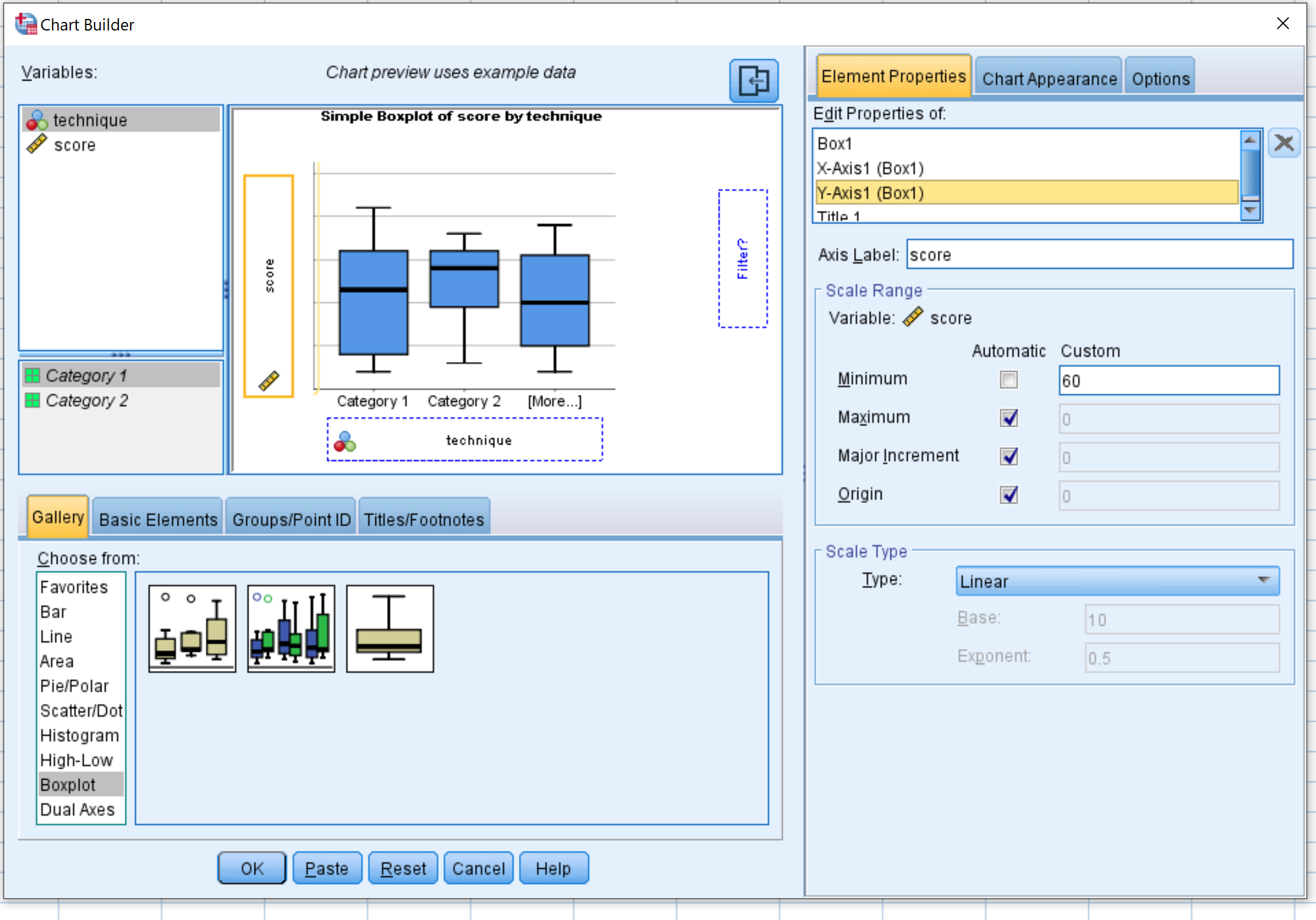
Selecione Boxplot na janela Escolher de:. Em seguida, arraste o primeiro gráfico denominado Boxplot simples para a janela principal de edição. Arraste a variável técnica no eixo x e a pontuação no eixo y.

Em seguida, clique em Propriedades do Elemento e em Eixo Y1 . Altere o valor mínimo para 60. Em seguida, clique em OK .

Os seguintes boxplots aparecerão:

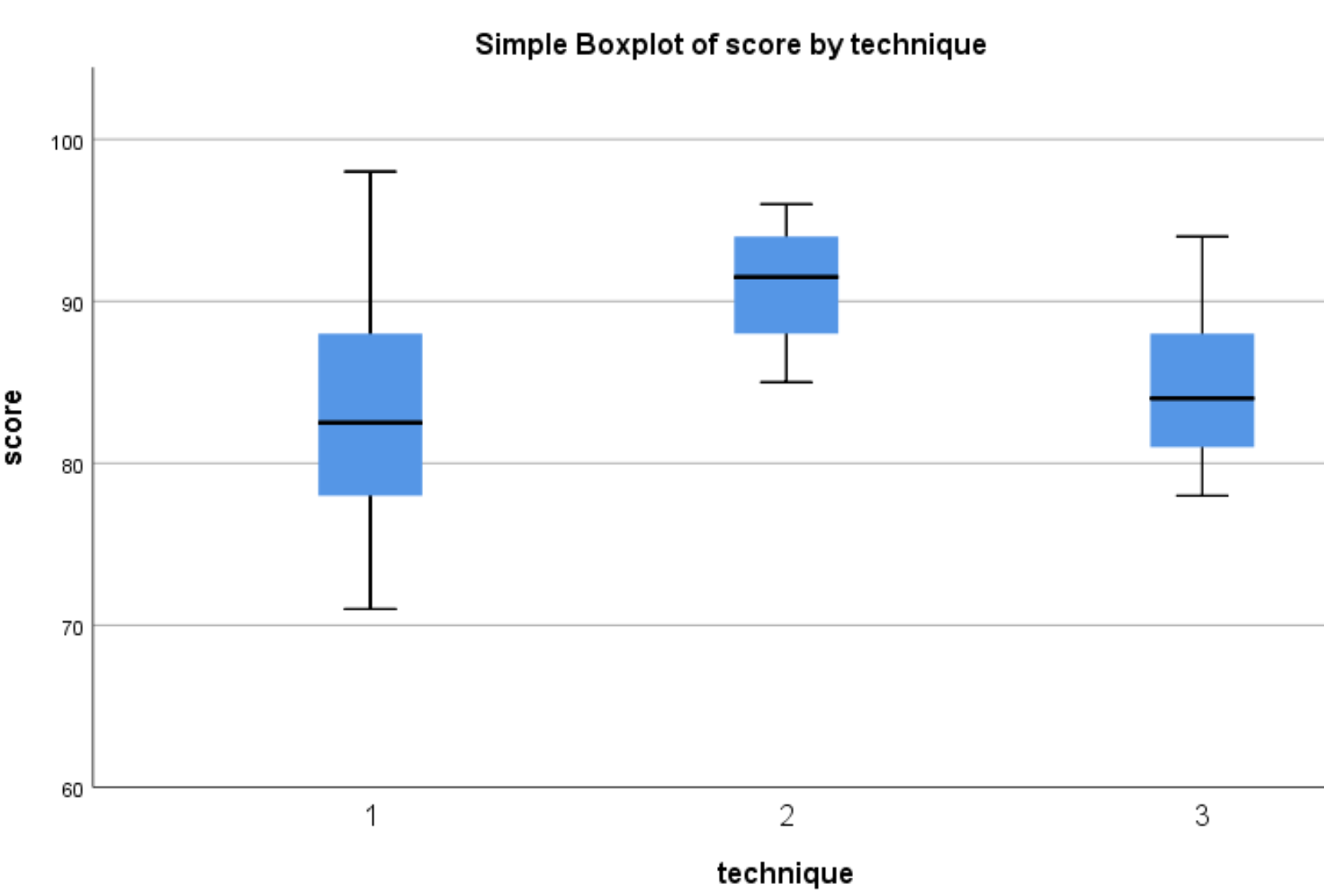
Podemos ver que a distribuição das pontuações dos testes tende a ser maior para os alunos que usaram a Técnica 2 do que para os alunos que usaram as Técnicas 1 e 3. Para determinar se essas diferenças de pontuação são estatisticamente significativas, realizaremos uma ANOVA unidirecional.

Etapa 2: execute uma ANOVA unidirecional.

Clique na guia Analisar , em seguida, em Comparar médias e em ANOVA unidirecional .

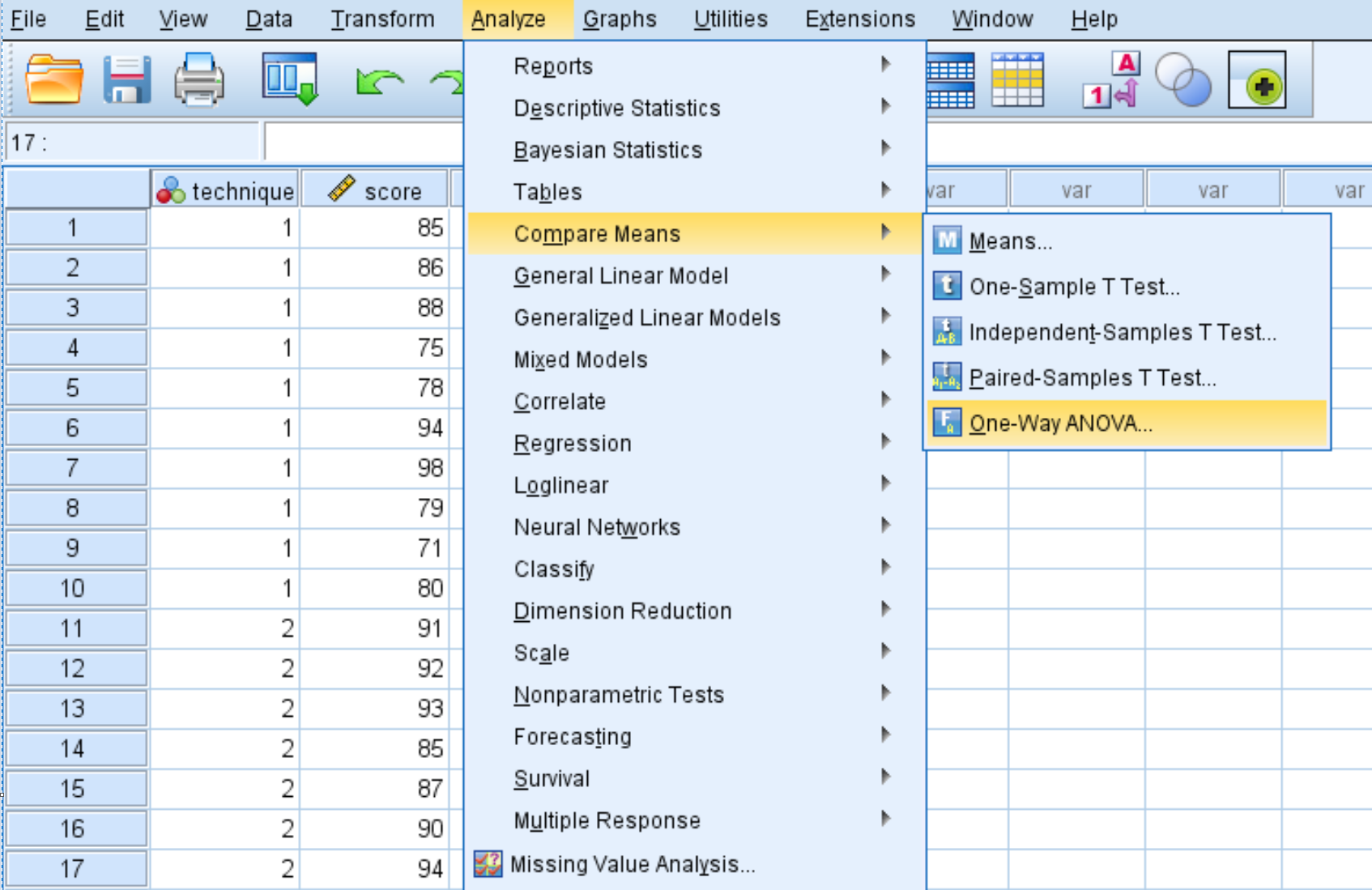
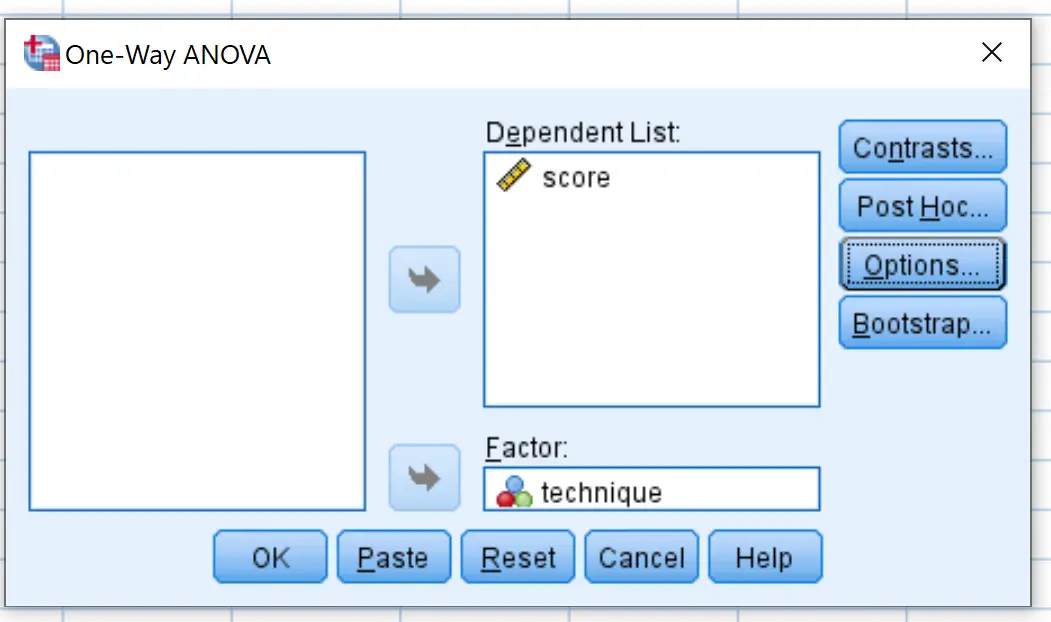
Na nova janela que aparece, coloque a variável pontuação na caixa denominada Lista de Dependentes e a variável técnica na caixa denominada Fator.

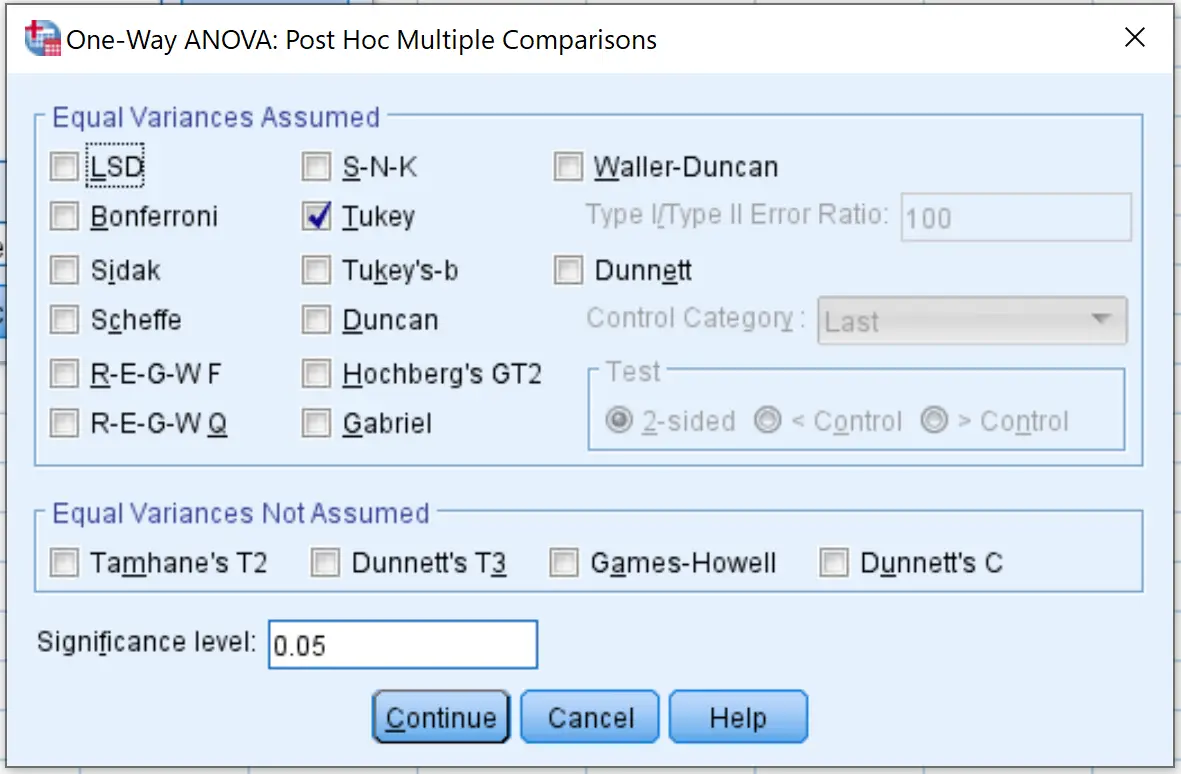
Em seguida, clique em Post Hoc e marque a caixa ao lado de Tukey . Em seguida, clique em Continuar .

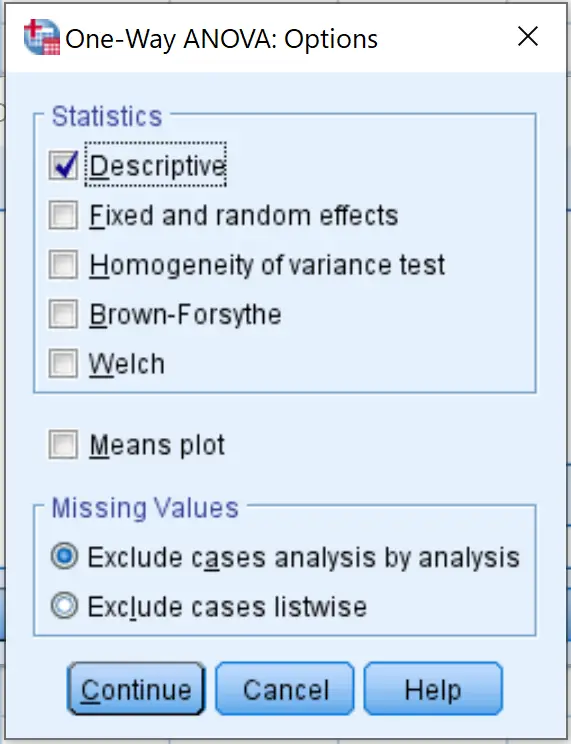
Em seguida, clique em Opções e marque a caixa ao lado de Descritivo . Em seguida, clique em Continuar .

Por fim, clique em OK .

Etapa 3: interprete o resultado.

Depois de clicar em OK , os resultados da ANOVA unidirecional aparecerão. Veja como interpretar o resultado:

Descrição da tabela

Esta tabela exibe estatísticas descritivas para cada um dos três grupos em nosso conjunto de dados.

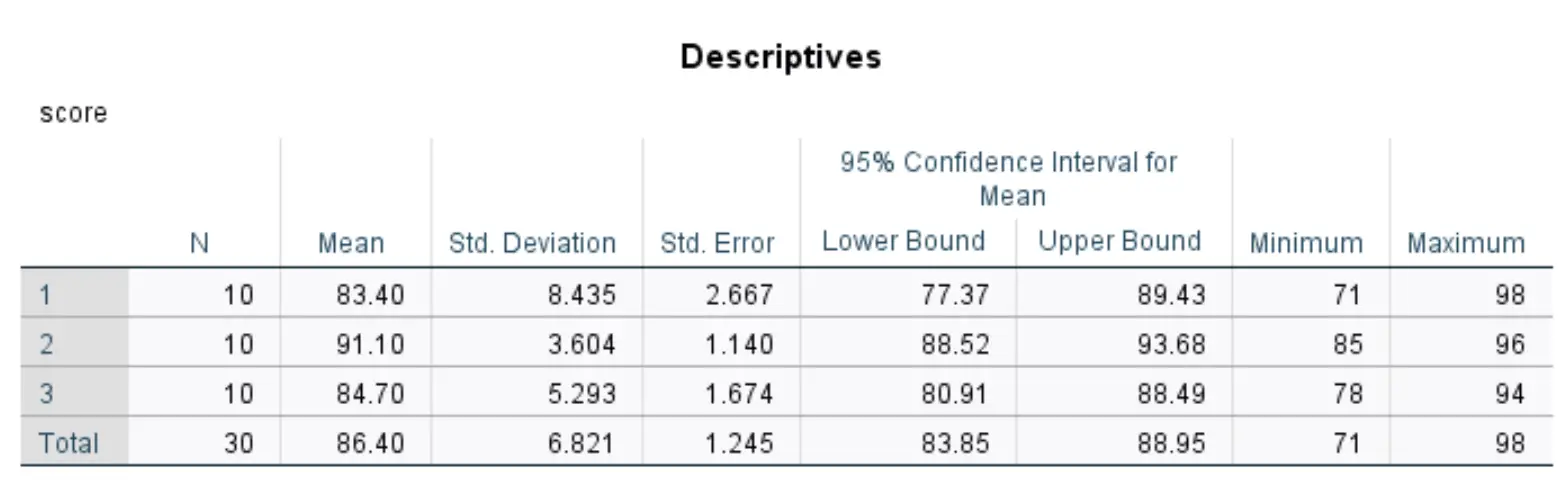
Os números mais relevantes incluem:

• N: O número de alunos em cada grupo.
• Média: A pontuação média do teste para cada grupo.
• Padrão. Desvio: Desvio padrão dos resultados dos testes para cada grupo.

Tabela ANOVA

Esta tabela exibe os resultados da ANOVA unidirecional:

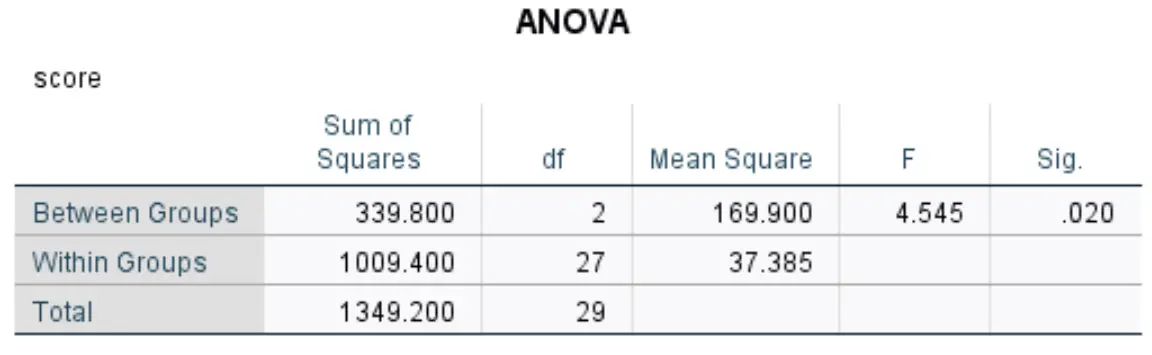
Os números mais relevantes incluem:

• F: A estatística F geral.
• Sig: O valor p que corresponde à estatística F (4,545) com o numerador df (2) e o denominador df (27). Nesse caso, o valor p acaba sendo 0,020 .

Lembre-se de que uma ANOVA unidirecional usa as seguintes hipóteses nulas e alternativas:

• H ₀ (hipótese nula): μ ₁ = μ ₂ = μ ₃ = … = μ _k (todas as médias populacionais são iguais)
• _HA (hipótese alternativa): pelo menos uma média populacional é diferente   descansar

Como o valor p da tabela ANOVA é inferior a 0,05, temos evidências suficientes para rejeitar a hipótese nula e concluir que pelo menos uma das médias do grupo é diferente das demais.

Para saber exatamente quais médias de grupos diferem entre si, podemos consultar a última tabela do resultado da ANOVA.

Tabela de comparação múltipla

Esta tabela exibe comparações múltiplas post-hoc de Tukey entre cada um dos três grupos. Estamos interessados principalmente na Sig. coluna, que exibe os valores p para as diferenças de médias entre cada grupo:

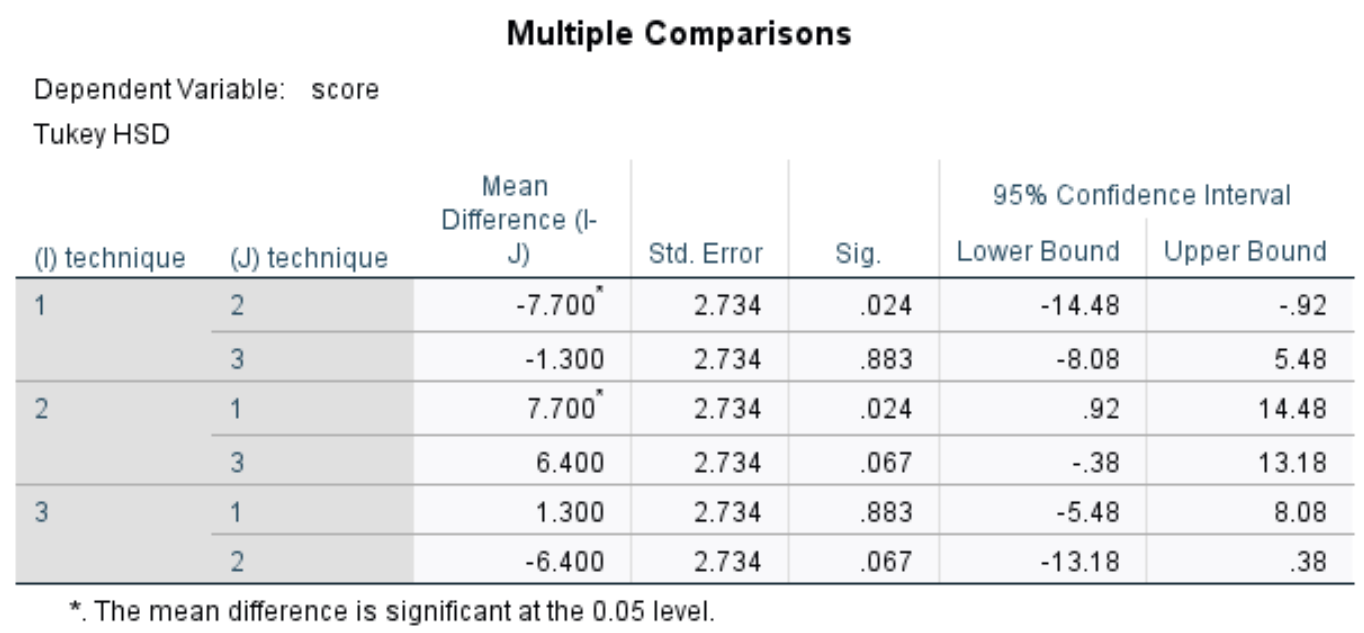
Na tabela podemos ver os valores p para as seguintes comparações:

• Técnica 1 contra 2: | valor p = 0,024
• Técnica 1 contra 3 | valor p = 0,883
• Técnica 2 contra 3 | valor p = 0,067

A única comparação de grupo com valor de p inferior a 0,05 é entre a Técnica 1 e a Técnica 2.

Isso nos diz que há uma diferença estatisticamente significativa nas notas médias dos testes entre os alunos que usaram a Técnica 1 e aqueles que usaram a Técnica 2.

Porém, não há diferença estatisticamente significativa entre as técnicas 1 e 3, nem entre as técnicas 2 e 3.

Etapa 4: relatar os resultados.

Finalmente, podemos relatar os resultados da ANOVA unidirecional. Aqui está um exemplo de como fazer isso:

Uma ANOVA unidirecional foi realizada para determinar se três técnicas de estudo diferentes levaram a resultados de teste diferentes.

Um total de 10 alunos usaram cada uma das três técnicas de estudo durante um mês antes de todos fazerem o mesmo teste.

Uma ANOVA unidirecional revelou que houve uma diferença estatisticamente significativa nas pontuações dos testes entre pelo menos dois grupos (F(2, 27) = 4,545, p = 0,020).

O teste de Tukey para comparações múltiplas revelou que as pontuações médias dos testes foram significativamente diferentes entre os alunos que usaram a Técnica 1 e a Técnica 2 (p = 0,024, IC 95% = [-14,48, -0,92]).

Não houve diferença estatisticamente significativa entre os escores das técnicas 1 e 3 (p = 0,883) ou entre os escores das técnicas 2 e 3 (p = 0,067).