Valor crítico

By Dr. benjamim anderson Agosto 3, 2023 Estatisticas 0 Comments

Este artigo explica qual é o valor crítico nas estatísticas e como ele deve ser interpretado nos testes de hipóteses. Da mesma forma, você poderá ver como o valor crítico é calculado, bem como vários exemplos concretos.

Qual é o valor crítico?

O valor crítico é o ponto na distribuição da estatística de teste que separa a região de rejeição da hipótese nula de sua região de aceitação. Ou seja, o valor crítico é o valor da distribuição do teste estatístico que marca o limite da região de rejeição (ou região crítica).

Normalmente, o valor crítico é representado pelo símbolo Z _α/2 , já que a distribuição de referência mais comum costuma ser a distribuição normal padrão .

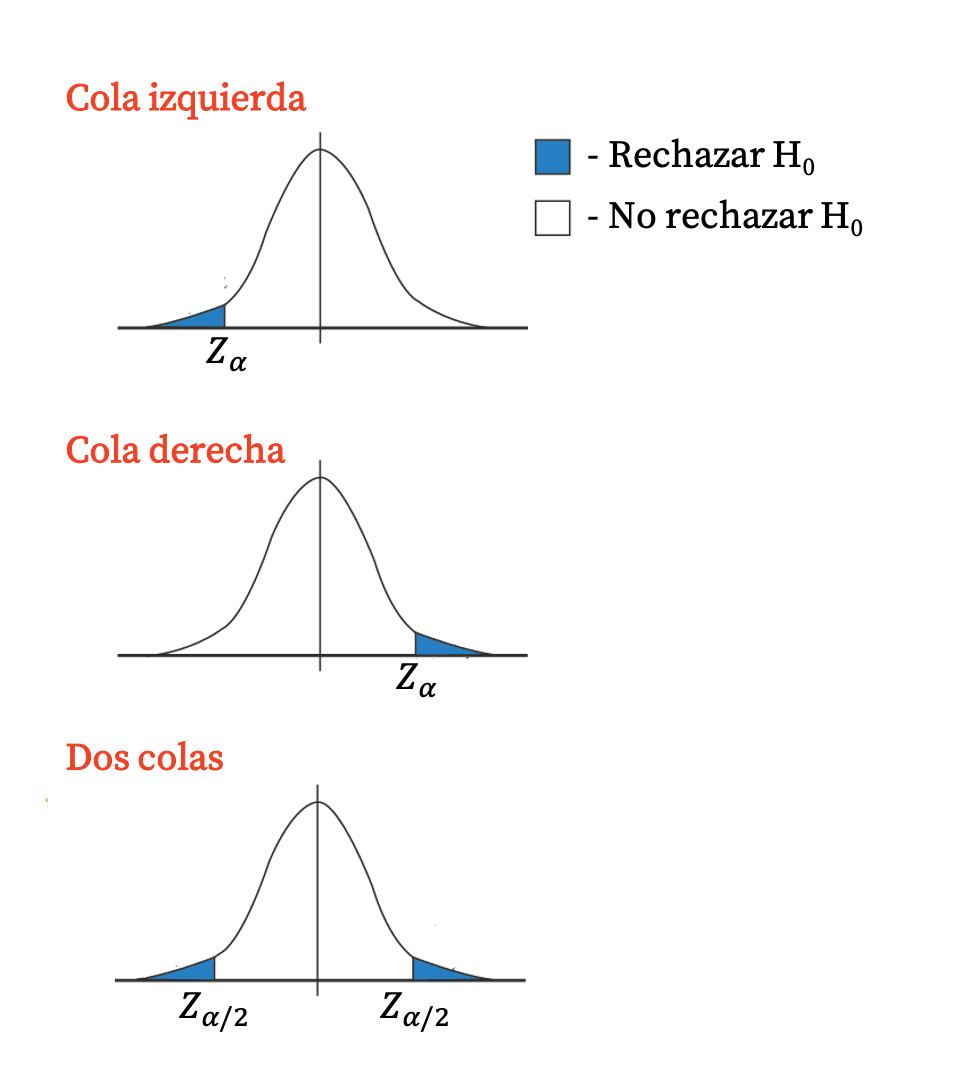
Em geral, os testes unilaterais são de valor crítico, uma vez que a região de rejeição constitui uma cauda única da distribuição. Por outro lado, os testes bicaudais possuem dois valores críticos, pois a região de rejeição corresponde a ambas as caudas da distribuição.

Nos intervalos de confiança , os valores críticos são os pontos da distribuição de referência que marcam os limites do intervalo de confiança.

Como calcular o valor crítico

Veremos então como são calculados os valores críticos mais comuns. O valor crítico de Z e o valor crítico de t são calculados para o intervalo de confiança da média, a única diferença é que o valor crítico de Z é calculado quando o desvio padrão da população é conhecido e, em vez disso, o valor crítico de t é usado quando apenas os dados de uma amostra são conhecidos.

Valor crítico de Z

O valor crítico de Z é usado para determinar os limites do intervalo de confiança da média. Mais precisamente, só é usado se você conhecer o desvio padrão da população.

Para calcular o valor crítico de Z, o valor correspondente à probabilidade de metade do nível de significância deve ser encontrado na tabela de distribuição normal padrão .

Por exemplo, se quisermos determinar um intervalo de confiança para a média com um nível de confiança de 95%, isto implica que o nível de significância é de 5%. Portanto, é necessário observar na tabela da distribuição normal padrão qual valor corresponde a uma probabilidade de 2,5%, já que o intervalo de confiança da média é bilateral.

$1-\alpha=0,95 \ \color{orange}\bm{\longrightarrow}\color{black} \ \alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}Z_{\alpha/2}= \ \color{orange}\bm{?}\\[4ex]Z_{0,025}=1,96\end{array}$

Abaixo você pode ver uma tabela com os valores Z críticos mais utilizados:

Nível de confiança (1-α)	Nível de significância (α)	Valor crítico (Z _α/2 )
0,80	0,20	1.282
0,85	0,15	1.440
0,90	0,10	1.645
0,95	0,05	1960
0,99	0,01	2.576
0,995	0,005	2.807
0,999	0,001	3.291

Valor crítico de t

O valor t crítico é usado para encontrar os limites do intervalo de confiança para a média quando o desvio padrão da população é desconhecido.

Para calcular o valor crítico de t, o valor correspondente à probabilidade de metade do nível de significância deve ser encontrado na tabela de distribuição t de Student , levando em consideração que os graus de liberdade da distribuição t de Student são de uma unidade. do que o tamanho da amostra.

Por exemplo, se quisermos encontrar o intervalo de confiança com nível de confiança de 95% e o tamanho da amostra for 8, precisamos acessar a tabela de distribuição t de Student e ver qual valor corresponde a t _0,025|7 .

$1-\alpha=0,95 \ \color{orange}\bm{\longrightarrow}\color{black} \ \alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}t_{\alpha/2| n-1}= \ \color{orange}\bm{?}\\[4ex]t_{0,025| 7}=2,365\end{array}$

➤ Veja: Como calcular o intervalo de confiança da média

O valor crítico no teste de hipóteses

O valor crítico também pode ser usado em testes de hipóteses para rejeitar a hipótese nula (e aceitar a hipótese alternativa) ou rejeitar a hipótese alternativa (e aceitar a hipótese nula).

Se o valor da distribuição da estatística de teste correspondente ao valor p estiver dentro do intervalo marcado pelos valores críticos, a hipótese nula não é rejeitada (a hipótese alternativa é rejeitada).
Se o valor da distribuição da estatística de teste correspondente ao valor-p estiver fora do intervalo marcado pelos valores críticos, a hipótese nula é rejeitada (a hipótese alternativa é aceita).

About Author

Dr. benjamim anderson

Olá, sou Benjamin, um professor aposentado de estatística que se tornou professor dedicado na Statorials. Com vasta experiência e conhecimento na área de estatística, estou empenhado em compartilhar meu conhecimento para capacitar os alunos por meio de Statorials. Saber mais