Como encontrar um valor p de uma pontuação t no excel

Freqüentemente, nas estatísticas, um teste de hipótese resultará em uma estatística de teste de pontuação T. Depois de encontrarmos esse escore t, geralmente encontramos o valor p associado a ele. Se este valor p estiver abaixo de um determinado nível alfa (por exemplo, 0,10, 0,05, 0,01), então rejeitamos a hipótese nula do teste e concluímos que nossos resultados são significativos.

Este tutorial explica como encontrar o valor p de uma pontuação t no Excel usando a função T.DIST , que recebe os seguintes argumentos:

DIST.T (x, graus_liberdade)

Ouro:

• x: A pontuação T que nos interessa.
• deg_freedom: Os graus de liberdade.

Vejamos alguns exemplos.

Exemplo 1: Valor P do escore t (bicaudal)

Um botânico quer saber se a altura média de uma determinada espécie de planta é igual a 15 polegadas. Em uma amostra aleatória de 12 plantas, ela descobre que a altura média da amostra é 14,33 polegadas e o desvio padrão da amostra é 1,37 polegadas.

Execute um teste de hipótese bicaudal usando um nível alfa de 0,05 para determinar se a altura média é igual a 15 polegadas.

Etapa 1: estabeleça as hipóteses.

A hipótese nula (H ₀ ): μ = 15

A hipótese alternativa: (Ha): μ ≠ 15

Etapa 2: Encontre a pontuação T e os graus de liberdade.

pontuação t = ( x -μ) / (s/√n) = (14,33-15) / (1,37/√12) = -1,694 .

graus de liberdade = n-1 = 12-1 = 11 .

Etapa 3: Encontre o valor p do escore t usando o Excel.

Para encontrar o valor p do escore t, usaremos a seguinte fórmula no Excel:

=DIST.T.2T(ABS(-1,694), 11)

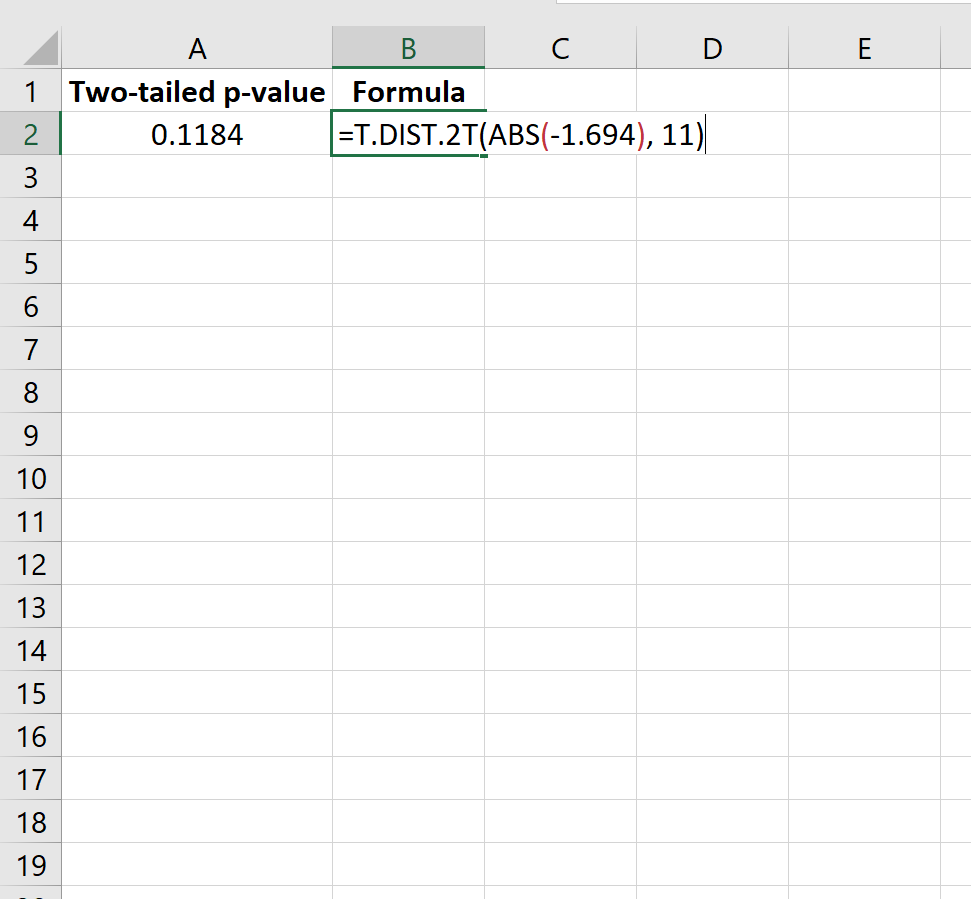
Isso nos diz que o valor p bilateral é 0,1184 .

Passo 4: Rejeite ou não rejeite a hipótese nula.

Como o valor p de 0,1184 não é inferior ao nível alfa escolhido de 0,05 , não conseguimos rejeitar a hipótese nula. Não temos evidências suficientes para dizer que a altura média das plantas seja diferente de 15 polegadas.

Exemplo 2: Valor P da pontuação T (unilateral)

Uma empresa quer saber se um novo tipo de bateria tem vida útil média mais longa do que a bateria padrão atual, que tem vida útil média de 18 horas. Numa amostra aleatória de 25 baterias novas, descobriram que a vida média é de 19 horas com um desvio padrão de 4 horas.

Execute um teste de hipótese unilateral usando um nível alfa de 0,05 para determinar se a vida média da nova bateria é maior que a vida média da bateria padrão atual.

Etapa 1: estabeleça as hipóteses.

A hipótese nula (H ₀ ): μ ≤ 18

A hipótese alternativa: (Ha): μ > 18

Etapa 2: Encontre a pontuação T e os graus de liberdade.

pontuação t = ( x -μ) / (s/√n) = (19-18) / (4/√25) = 1,25 .

graus de liberdade = n-1 = 25-1 = 24 .

Etapa 3: Encontre o valor p do escore t usando o Excel.

Para encontrar o valor p do escore t, usaremos a seguinte fórmula no Excel:

=T.DIST.RT(1,25, 24)

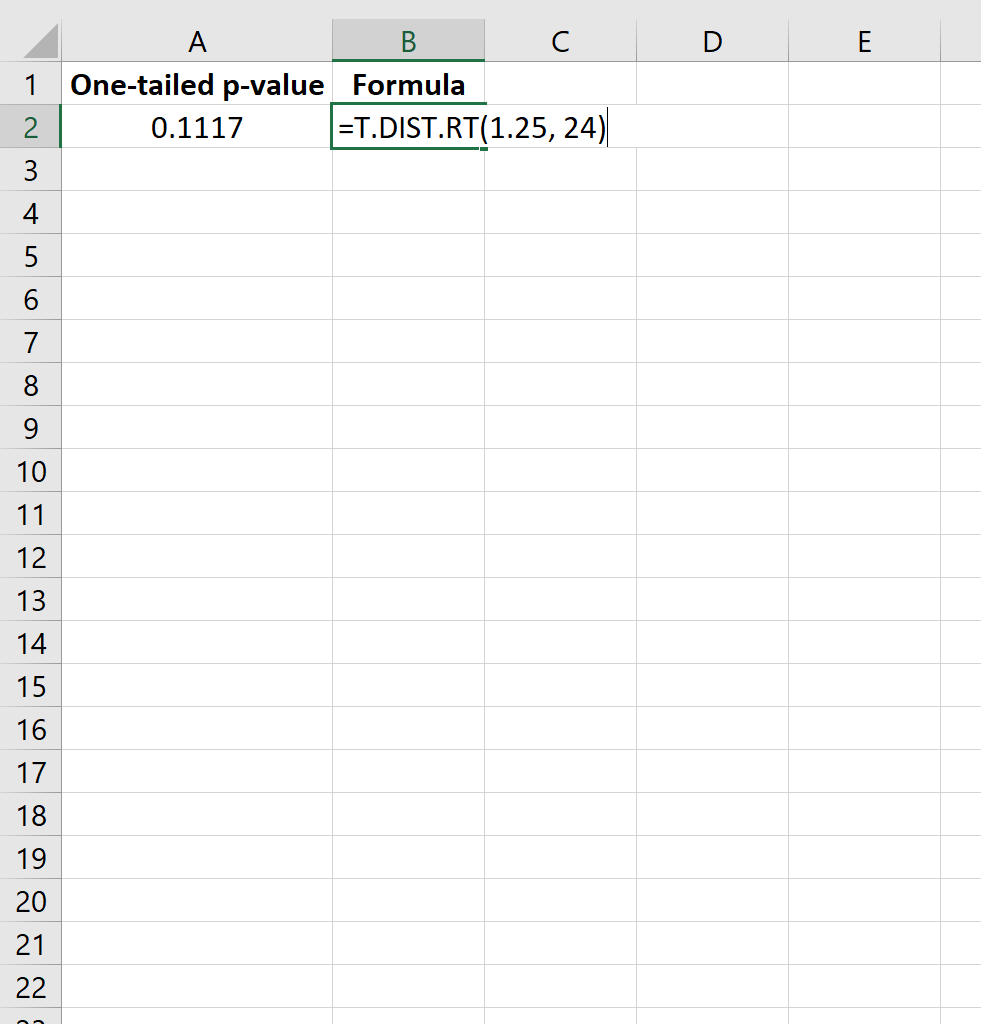
Isso nos diz que o valor p unilateral é 0,1117 .

Passo 4: Rejeite ou não rejeite a hipótese nula.

Como o valor p de 0,1117 é maior que o nível alfa escolhido de 0,05 , não conseguimos rejeitar a hipótese nula. Não temos provas suficientes para afirmar que a vida média da nova bateria seja superior à vida média da bateria padrão atual.

Para mais tutoriais sobre estatísticas no Excel, não deixe de conferir nossa lista completa de guias do Excel .