O intervalo interquartil (iqr) é afetado por valores discrepantes?

Nas estatísticas, muitas vezes queremos saber até que ponto os valores estão “dispersos” em uma distribuição.

Uma forma popular de medir o spread é o intervalo interquartil , que é calculado como a diferença entre o primeiro quartil e o terceiro quartil de um conjunto de dados. Quartis são simplesmente valores que dividem um conjunto de dados em quatro partes iguais.

Exemplo: Cálculo do intervalo interquartil

O exemplo a seguir mostra como calcular o intervalo interquartil para um determinado conjunto de dados:

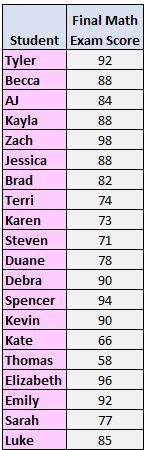
Passo 1: Organize os valores do menor para o maior.

58, 66, 71, 73, 74, 77, 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98

2. Encontre a mediana.

58, 66, 71, 73, 74, 77 , 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98

Neste caso, a mediana está entre 85 e 88.

3. A mediana divide o conjunto de dados em duas metades. A mediana da metade inferior é o quartil inferior e a mediana da metade superior é o quartil superior:

58, 66, 71, 73, 74 , 77, 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98

4. Calcule o intervalo interquartil.

Nesse caso, o primeiro quartil é a média dos dois valores intermediários na metade inferior do conjunto de dados (75,5) e o terceiro quartil é a média dos dois valores intermediários na metade superior do conjunto de dados (91).

Portanto, o intervalo interquartil é 91 – 75,5 = 15,5

O intervalo interquartil não é afetado por valores discrepantes

Uma das razões pelas quais as pessoas preferem usar o intervalo interquartil (IQR) ao calcular o “spread” de um conjunto de dados é que ele é robusto a valores discrepantes. Como o IQR é simplesmente o intervalo intermediário de 50% dos valores dos dados, ele não é afetado porvalores discrepantes extremos .

Para demonstrar isso, considere o seguinte conjunto de dados:

[1, 4, 8, 11, 13, 17, 17, 20]

Aqui estão as diferentes métricas de propagação para este conjunto de dados:

• Intervalo interquartil: 11
• Alcance: 19
• Desvio padrão: 6,26
• Diferença: 39,23

Agora considere o mesmo conjunto de dados, mas com um valor discrepante extremo adicionado:

[1, 4, 8, 11, 13, 17, 17, 20, 150 ]

Aqui estão as diferentes métricas de propagação para este conjunto de dados:

• Intervalo interquartil: 12,5
• Alcance: 149
• Desvio padrão: 43,96
• Spread: 1.932,84

Observe como o intervalo interquartil muda apenas ligeiramente, de 11 para 12,5. Contudo, todas as outras medidas de dispersão mudam dramaticamente.

Isto demonstra que o intervalo interquartil não é afetado por valores discrepantes como outras medidas de dispersão. Por esse motivo, é uma forma confiável de medir a distribuição dos 50% intermediários dos valores em qualquer distribuição.

Leitura adicional:

Medições de dispersão
Calculadora de intervalo interquartil