Qual é a lacuna residual? (definição e #038; exemplo)

A variância residual (às vezes chamada de “variância inexplicável”) refere-se à variância em um modelo que não pode ser explicada pelas variáveis do modelo.

Quanto maior a variância residual de um modelo, menos o modelo é capaz de explicar a variação nos dados.

A variância residual aparece nos resultados de dois modelos estatísticos diferentes:

1. ANOVA: utilizada para comparar médias de três ou mais grupos independentes.

2. Regressão: usada para quantificar a relação entre uma ou mais variáveis preditoras e uma variável resposta .

Os exemplos a seguir mostram como interpretar a variância residual em cada um desses métodos.

Variância residual em modelos ANOVA

Cada vez que ajustamos um modelo ANOVA (“análise de variância”), obtemos uma tabela ANOVA semelhante a esta:

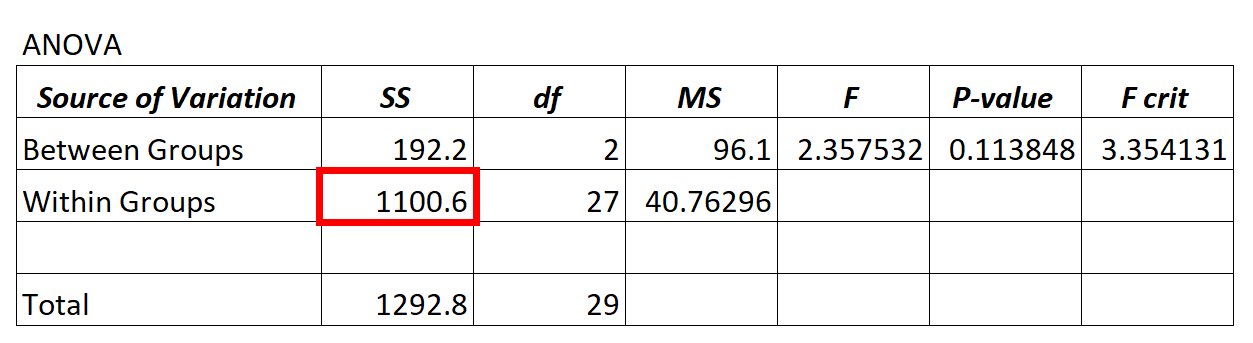
O valor da variância residual do modelo ANOVA é encontrado na coluna SS (“soma dos quadrados”) para variação dentro do grupo .

Este valor também é chamado de “soma dos erros quadráticos” e é calculado usando a seguinte fórmula:

Σ(X _ij – X _j ) ²

Ouro:

• Σ : um símbolo grego que significa “soma”
• X _ij : a ^i-ésima observação do grupo j
• X _j : a média do grupo j

No modelo ANOVA acima, vemos que a variância residual é 1100,6.

Para determinar se esta variância residual é “alta”, podemos calcular a soma média dos quadrados dentro dos grupos e a soma média dos quadrados entre os grupos e encontrar a razão entre os dois, o que dá o valor F geral na tabela ANOVA.

• F = MS _entra / MS _entra
• F = 96,1/40,76296
• F = 2,357

O valor F na tabela ANOVA acima é 2,357 e o valor p correspondente é 0,113848. Como este valor p não é inferior a α = 0,05, não temos evidências suficientes para rejeitar a hipótese nula.

Isto significa que não temos evidências suficientes para dizer que a diferença média entre os grupos que estamos comparando é significativamente diferente.

Isto diz-nos que a variância residual do modelo ANOVA é elevada em comparação com a variação que o modelo pode realmente explicar.

Variância residual em modelos de regressão

Num modelo de regressão, a variância residual é definida como a soma dos quadrados das diferenças entre os pontos de dados previstos e os pontos de dados observados.

É calculado da seguinte forma:

Σ(ŷ _eu – y _eu ) ²

Ouro:

• Σ : um símbolo grego que significa “soma”
• ŷ _i : Os pontos de dados previstos
• y _i : Os pontos de dados observados

Quando ajustamos um modelo de regressão, geralmente obtemos um resultado semelhante ao seguinte:

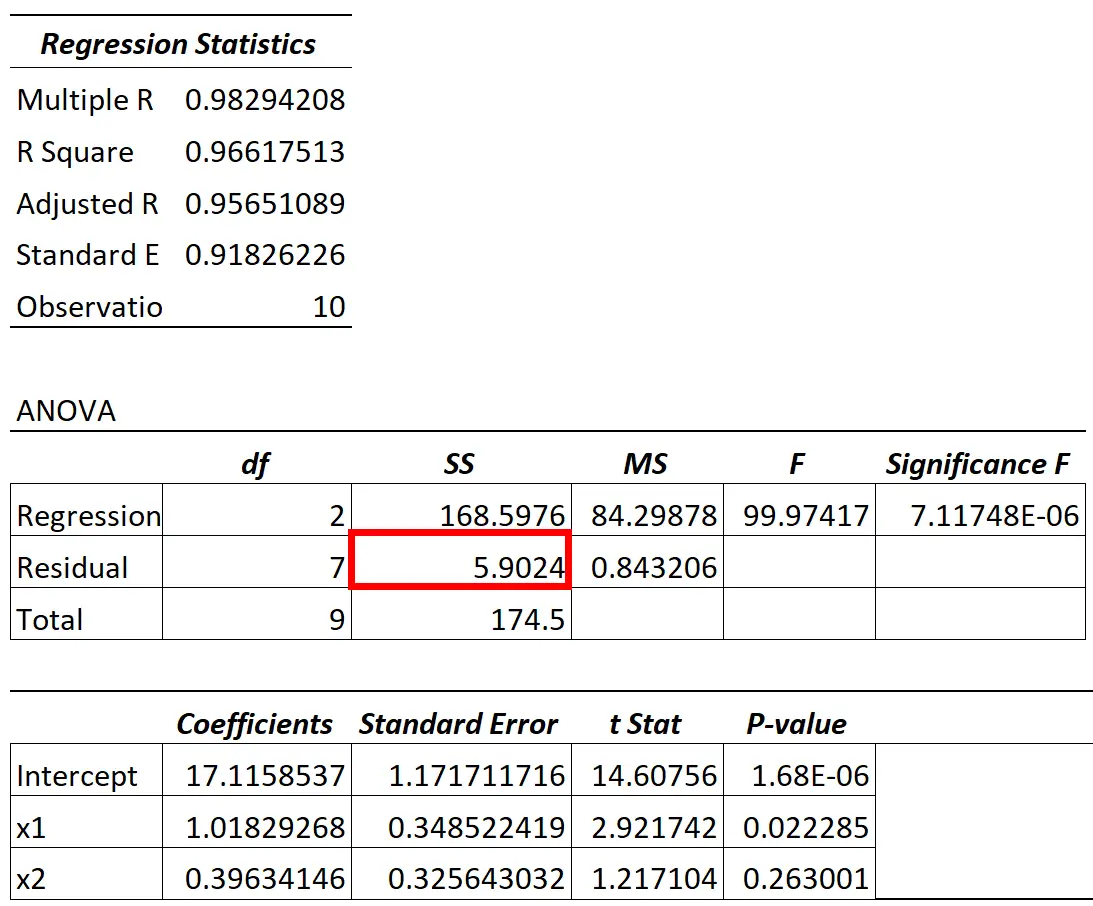
O valor da variância residual do modelo ANOVA pode ser encontrado na coluna SS (“soma dos quadrados”) para variação residual.

A razão entre a variação residual e a variação total no modelo nos diz a porcentagem de variação na variável resposta que não pode ser explicada pelas variáveis preditoras no modelo.

Por exemplo, na tabela acima, calcularíamos esse percentual da seguinte forma:

• Variação inexplicada = SS Residual / SS Total
• Variação inexplicada = 5,9024 / 174,5
• Variação inexplicada = 0,0338

Este valor também pode ser calculado usando a seguinte fórmula:

• Variação inexplicada = 1 – R ²
• Variação inexplicada = 1 – 0,96617
• Variação inexplicada = 0,0338

O valor R-quadrado do modelo nos diz a porcentagem de variação na variável resposta que pode ser explicada pela variável preditora.

Assim, quanto menor a variação inexplicada, mais capaz é o modelo de utilizar as variáveis preditoras para explicar a variação na variável resposta.

Recursos adicionais

O que é um bom valor de R ao quadrado?
Como calcular R-quadrado no Excel
Como calcular R ao quadrado em R