Como usar variáveis fictícias na análise de regressão

A regressão linear é um método que podemos usar para quantificar a relação entre uma ou mais variáveis preditoras e uma variável de resposta .

Geralmente usamos regressão linear com variáveis quantitativas . Às vezes chamadas de variáveis “numéricas”, são variáveis que representam uma quantidade mensurável. Exemplos incluem:

• Número de metros quadrados em uma casa
• Tamanho populacional de uma cidade
• Idade de um indivíduo

No entanto, às vezes queremos usar variáveis categóricas como variáveis preditoras. São variáveis que recebem nomes ou rótulos e podem ser divididas em categorias. Exemplos incluem:

• Cor dos olhos (por exemplo, “azul”, “verde”, “castanho”)
• Gênero (por exemplo, “homem”, “mulher”)
• Estado civil (por exemplo, “casado”, “solteiro”, “divorciado”)

Ao usar variáveis categóricas, não faz sentido apenas atribuir valores como 1, 2, 3 a valores como “azul”, “verde” e “marrom”, porque não faz sentido dizer esse verde é duplo. tão colorido quanto o azul ou o marrom é três vezes mais colorido que o azul.

Em vez disso, a solução é usar variáveis fictícias . São variáveis que criamos especificamente para análise de regressão e que assumem um de dois valores: zero ou um.

Variáveis dummy: Variáveis numéricas usadas na análise de regressão para representar dados categóricos que só podem assumir um de dois valores: zero ou um.

O número de variáveis fictícias que precisamos criar é igual a k -1 onde k é o número de valores diferentes que a variável categórica pode assumir.

Os exemplos a seguir ilustram como criar variáveis fictícias para diferentes conjuntos de dados.

Exemplo 1: Crie uma variável fictícia com apenas dois valores

Suponha que temos o seguinte conjunto de dados e queremos usar gênero e idade para prever a renda :

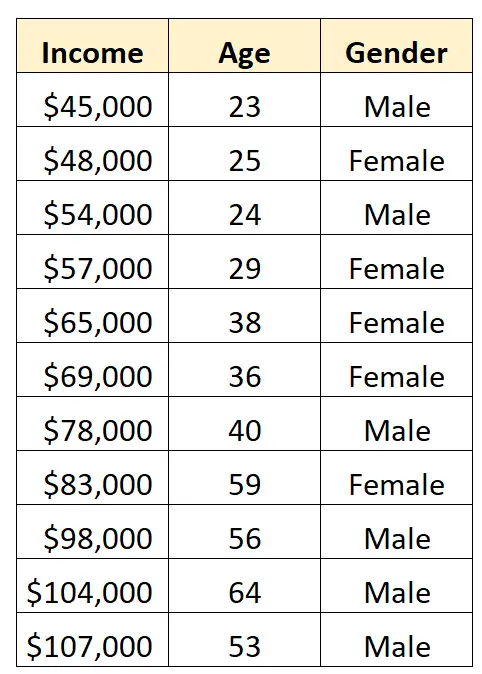
Para usar o gênero como variável preditora em um modelo de regressão, precisamos convertê-lo em uma variável fictícia.

Como esta é atualmente uma variável categórica que pode assumir dois valores diferentes (“Masculino” ou “Feminino”), simplesmente criamos k -1 = 2-1 = 1 variável fictícia.

Para criar esta variável dummy, podemos escolher um dos valores (“Masculino” ou “Feminino”) para representar 0 e outro para representar 1.

Em geral, costumamos representar o valor mais frequente com 0, que seria “Masculino” neste conjunto de dados.

Então, veja como converter gênero em uma variável fictícia:

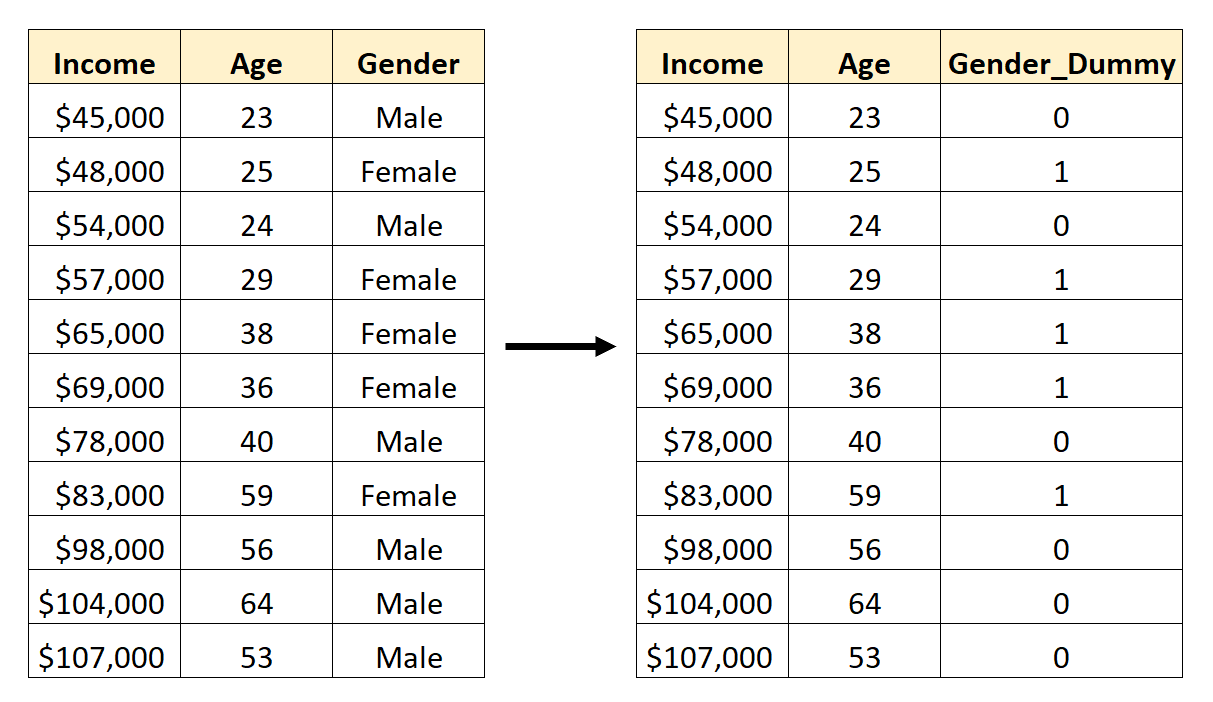
Poderíamos então usar Idade e Gênero_Dummy como variáveis preditoras em um modelo de regressão.

Exemplo 2: Crie uma variável fictícia com vários valores

Digamos que temos o seguinte conjunto de dados e queremos usar o estado civil e a idade para prever a renda :

Para usar o estado civil como variável preditora em um modelo de regressão, precisamos convertê-lo em uma variável dummy.

Como esta é atualmente uma variável categórica que pode assumir três valores diferentes (“Solteiro”, “Casado” ou “Divorciado”), precisamos criar k -1 = 3-1 = 2 variáveis fictícias.

Para criar esta variável fictícia, podemos deixar “Single” como valor base, pois ele aparece com mais frequência. Então, aqui está como converteríamos o estado civil em variáveis fictícias:

Poderíamos então usar Idade , Casado e Divorciado como variáveis preditoras em um modelo de regressão.

Como interpretar a saída da regressão com variáveis fictícias

Suponha que ajustamos um modelo de regressão linear múltipla usando o conjunto de dados do exemplo anterior com Idade , Casado e Divorciado como variáveis preditoras e Renda como variável de resposta.

Aqui está o resultado da regressão:

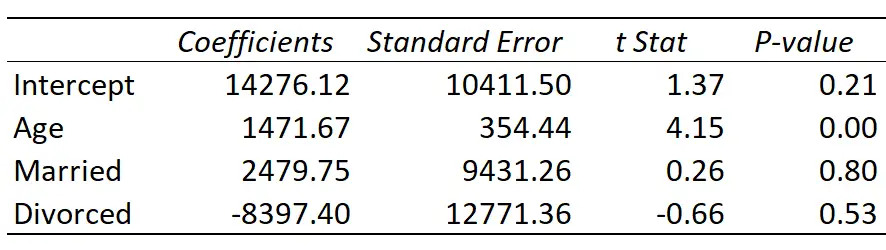
A linha de regressão ajustada é definida como:

Renda = 14.276,21 + 1.471,67*(Idade) + 2.479,75*(Casado) – 8.397,40*(Divorciado)

Podemos usar esta equação para encontrar a renda estimada de um indivíduo com base em sua idade e estado civil. Por exemplo, uma pessoa de 35 anos e casada teria uma renda estimada de US$ 68.264 :

Renda = 14.276,21 + 1.471,67*(35) + 2.479,75*(1) – 8.397,40*(0) = $ 68.264

Veja como interpretar os coeficientes de regressão na tabela:

• Intercepto: O intercepto representa a renda média de uma pessoa solteira com zero anos. Obviamente você não pode ter zero anos, então não faz sentido interpretar a interceptação por si só neste modelo de regressão específico.
• Idade: Cada ano de aumento na idade está associado a um aumento médio de US$ 1.471,67 na renda. Como o valor p (0,00) é inferior a 0,05, a idade é um preditor de renda estatisticamente significativo.
• Casado: Uma pessoa casada ganha em média US$ 2.479,75 a mais do que uma pessoa solteira. Como o valor p (0,80) não é inferior a 0,05, esta diferença não é estatisticamente significativa.
• Divorciado: Uma pessoa divorciada ganha em média $ 8.397,40 menos do que uma pessoa solteira. Como o valor p (0,53) não é inferior a 0,05, esta diferença não é estatisticamente significativa.

Como ambas as variáveis dummy não foram estatisticamente significativas, poderíamos remover o estado civil como preditor do modelo, uma vez que não parece agregar valor preditivo à renda.

Recursos adicionais

Variáveis qualitativas e quantitativas
A armadilha variável fictícia
Como ler e interpretar uma tabela de regressão
Uma explicação dos valores P e significância estatística